Elliptic Curve Cryptography (ECC) offers enhanced security with smaller key sizes compared to traditional cryptographic methods, making it ideal for resource-constrained devices. Its efficiency and strength stem from the mathematical properties of elliptic curves over finite fields, widely used in secure communications and digital signatures. Discover how ECC can strengthen your data protection by exploring its principles and applications further in the article.
Table of Comparison
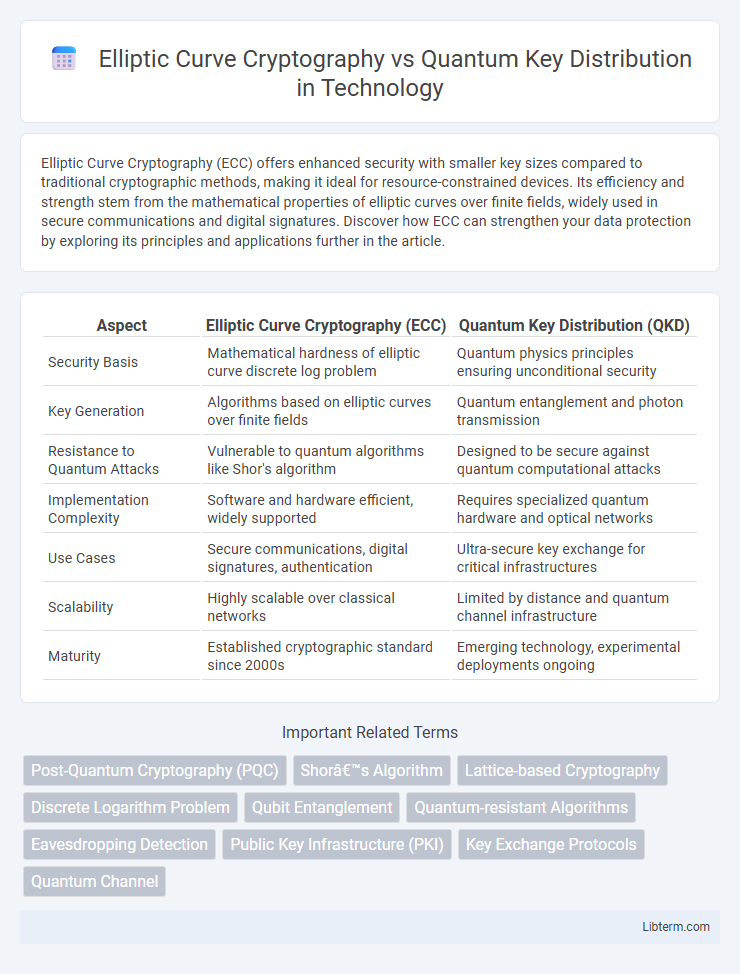
| Aspect | Elliptic Curve Cryptography (ECC) | Quantum Key Distribution (QKD) |
|---|---|---|
| Security Basis | Mathematical hardness of elliptic curve discrete log problem | Quantum physics principles ensuring unconditional security |
| Key Generation | Algorithms based on elliptic curves over finite fields | Quantum entanglement and photon transmission |
| Resistance to Quantum Attacks | Vulnerable to quantum algorithms like Shor's algorithm | Designed to be secure against quantum computational attacks |
| Implementation Complexity | Software and hardware efficient, widely supported | Requires specialized quantum hardware and optical networks |
| Use Cases | Secure communications, digital signatures, authentication | Ultra-secure key exchange for critical infrastructures |
| Scalability | Highly scalable over classical networks | Limited by distance and quantum channel infrastructure |
| Maturity | Established cryptographic standard since 2000s | Emerging technology, experimental deployments ongoing |
Introduction to Secure Communication Technologies
Elliptic Curve Cryptography (ECC) leverages the algebraic structure of elliptic curves over finite fields to provide robust encryption with smaller key sizes, enhancing computational efficiency and security in digital communication. Quantum Key Distribution (QKD) utilizes principles of quantum mechanics, such as superposition and entanglement, to enable theoretically unbreakable key exchange by detecting eavesdropping attempts in real-time. Both technologies represent critical advances in secure communication, with ECC serving as a widely adopted classical cryptographic method and QKD offering emerging quantum-resistant solutions for future-proof security.
Overview of Elliptic Curve Cryptography (ECC)
Elliptic Curve Cryptography (ECC) leverages the mathematical properties of elliptic curves over finite fields to create cryptographic keys, offering strong security with smaller key sizes compared to traditional methods like RSA. ECC's efficiency in key generation, encryption, and digital signatures makes it ideal for resource-constrained environments such as mobile devices and IoT. The underlying elliptic curve discrete logarithm problem provides a high level of cryptographic strength, although it remains vulnerable to potential quantum computing attacks.
Fundamentals of Quantum Key Distribution (QKD)
Quantum Key Distribution (QKD) leverages quantum mechanics principles such as superposition and entanglement to enable secure communication by detecting eavesdropping attempts during key exchange. Unlike Elliptic Curve Cryptography (ECC), which relies on mathematical complexity, QKD provides information-theoretic security grounded in the physical laws of quantum particles. Protocols like BB84 and E91 demonstrate how QKD generates and distributes encryption keys with guaranteed secrecy, ensuring robustness against quantum computer attacks.
Security Principles of ECC
Elliptic Curve Cryptography (ECC) relies on the mathematical difficulty of the Elliptic Curve Discrete Logarithm Problem (ECDLP) to provide strong security with smaller key sizes compared to traditional methods. The security principles of ECC are based on the use of elliptic curves over finite fields, enabling efficient encryption, digital signatures, and key exchange while maintaining robustness against classical computational attacks. Unlike Quantum Key Distribution (QKD), ECC's security depends on computational assumptions rather than physics, making it vulnerable to future quantum algorithms but currently practical for widespread cryptographic use.
Security Protocols in QKD
Elliptic Curve Cryptography (ECC) relies on the mathematical difficulty of the elliptic curve discrete logarithm problem to secure digital communications, while Quantum Key Distribution (QKD) uses principles of quantum mechanics, such as quantum entanglement and no-cloning theorem, to enable theoretically unbreakable key exchange. Security protocols in QKD, including BB84 and E91, ensure that any eavesdropping attempt alters the quantum states, instantly revealing the intrusion and guaranteeing unconditional security. Unlike ECC, which could be vulnerable to quantum computing attacks, QKD's protocols leverage quantum properties to provide secure key distribution immune to computational advances.
Performance and Scalability: ECC vs QKD
Elliptic Curve Cryptography (ECC) offers high performance with efficient key generation and encryption processes suitable for resource-constrained devices, making it scalable across various digital platforms. Conversely, Quantum Key Distribution (QKD) requires specialized quantum hardware and limited fiber-optic or free-space channels, resulting in lower throughput and scalability challenges. ECC's software-based implementation supports widespread adoption in large-scale networks, while QKD is currently confined to niche, high-security applications due to infrastructure and distance limitations.
Resistance to Quantum Attacks
Elliptic Curve Cryptography (ECC) relies on the hardness of the elliptic curve discrete logarithm problem, which is vulnerable to Shor's algorithm running on sufficiently powerful quantum computers, compromising its security. Quantum Key Distribution (QKD) leverages principles of quantum mechanics, such as quantum entanglement and no-cloning theorem, to provide theoretically unbreakable encryption immune to quantum attacks. As quantum computing advances threaten classical cryptographic schemes like ECC, QKD offers a future-proof solution for secure communication resistant to quantum adversaries.
Practical Implementation Challenges
Elliptic Curve Cryptography (ECC) faces practical implementation challenges such as vulnerability to side-channel attacks and the need for efficient key management in constrained environments. Quantum Key Distribution (QKD) requires specialized quantum hardware, including photon detectors and entangled photon sources, which complicates scalable deployment and integration with existing communication infrastructure. Both technologies confront distinct operational hurdles, with ECC's classical hardware compatibility contrasting QKD's reliance on fragile quantum states and dedicated infrastructure.
Use Cases and Industry Adoption
Elliptic Curve Cryptography (ECC) is extensively used in digital signatures, secure web communications (TLS/SSL), and cryptocurrency transactions due to its efficiency and strong security with smaller key sizes. Quantum Key Distribution (QKD) is primarily adopted in government, military, and high-security sectors for future-proofing data transmission against quantum computing threats by providing theoretically unbreakable encryption. While ECC remains dominant in mainstream commercial applications and IoT devices, QKD's adoption is growing in specialized industries like defense and financial institutions requiring ultra-secure communication channels.
Future Outlook: ECC and QKD in Post-Quantum Era
Elliptic Curve Cryptography (ECC) faces increasing vulnerability due to advances in quantum computing, necessitating the exploration of Quantum Key Distribution (QKD) as a complementary technology for secure communication. QKD offers theoretically unbreakable encryption by leveraging quantum mechanics principles, making it a promising solution for post-quantum cryptography. Integrating ECC with QKD protocols could enhance cryptographic resilience, ensuring secure data exchange in the emerging post-quantum era.
Elliptic Curve Cryptography Infographic
 libterm.com
libterm.com