Ternary Search Trees (TST) combine the efficient search capabilities of binary search trees with the character-by-character traversal of tries, making them ideal for storing and retrieving strings. With nodes that have three children--less, equal, and greater--TSTs efficiently handle prefix matching and autocomplete functions while optimizing space compared to traditional tries. Explore the rest of the article to discover how Ternary Search Trees can enhance your string processing needs.
Table of Comparison
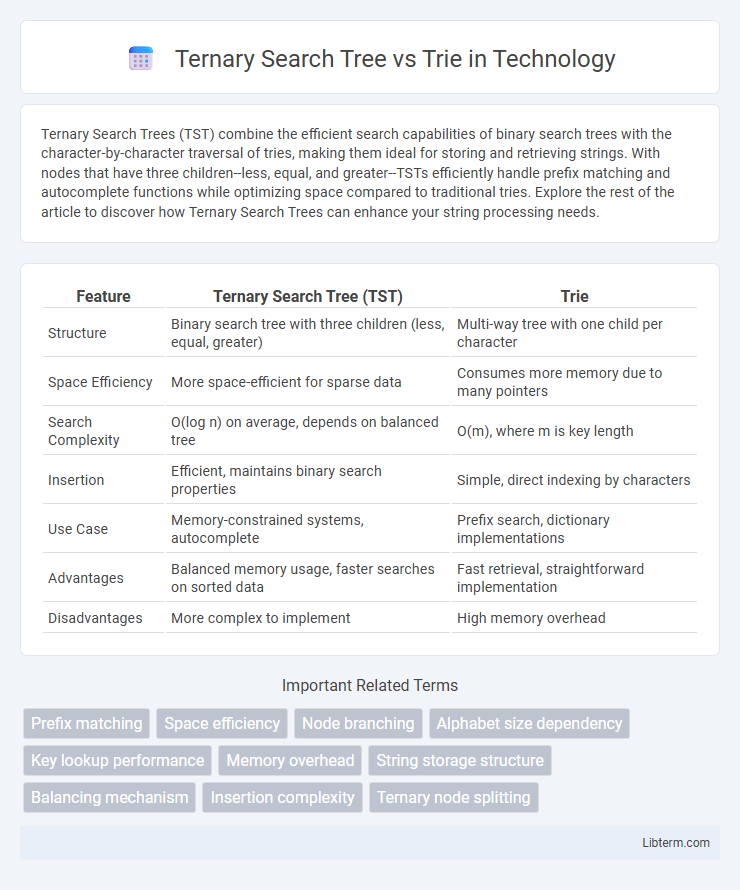
| Feature | Ternary Search Tree (TST) | Trie |
|---|---|---|
| Structure | Binary search tree with three children (less, equal, greater) | Multi-way tree with one child per character |
| Space Efficiency | More space-efficient for sparse data | Consumes more memory due to many pointers |
| Search Complexity | O(log n) on average, depends on balanced tree | O(m), where m is key length |
| Insertion | Efficient, maintains binary search properties | Simple, direct indexing by characters |
| Use Case | Memory-constrained systems, autocomplete | Prefix search, dictionary implementations |
| Advantages | Balanced memory usage, faster searches on sorted data | Fast retrieval, straightforward implementation |
| Disadvantages | More complex to implement | High memory overhead |
Introduction to Ternary Search Trees and Tries
Ternary Search Trees (TSTs) store characters in nodes with three children, allowing efficient storage and retrieval of strings by combining benefits of binary search trees and tries. Tries organize strings in a tree structure where each node represents a character, enabling fast prefix-based searches but often consuming more memory. TSTs use less space than tries while maintaining comparable search times, making them suitable for applications like autocomplete and spell checking.
Data Structure Overview: TST vs Trie
Ternary Search Trees (TST) combine characteristics of binary search trees and tries, using nodes with three pointers to manage characters, optimizing space for sparse datasets. Tries, or prefix trees, maintain children in arrays or hash maps for each character, allowing fast prefix-based searches but often consuming more memory. TSTs offer balanced search times with less memory overhead compared to tries, making them suitable for memory-constrained environments.
Memory Usage Comparison
Ternary Search Trees (TSTs) offer a more memory-efficient structure than Tries by using nodes with three children, significantly reducing pointer overhead compared to Tries that allocate a pointer for every possible character in the alphabet. Tries require large arrays at each node, leading to high memory consumption especially for sparse datasets or large alphabets, whereas TSTs dynamically allocate child nodes only when necessary. This efficient memory usage makes TSTs preferable in applications with limited memory resources or extensive alphabets, balancing search performance with storage constraints.
Search and Insertion Efficiency
Ternary Search Trees (TSTs) offer balanced search and insertion times with average-case complexity of O(log n) due to their tree-like structure, making them space-efficient for sparse datasets. Tries provide faster search and insertion at O(m), where m is the length of the key, by leveraging direct character-by-character node traversal, but they consume more memory due to storing multiple child pointers per node. For applications requiring efficient prefix searches and fast lookup with moderate memory usage, TSTs provide a good trade-off, whereas Tries excel in scenarios demanding constant-time search regardless of data sparsity.
Lookup Performance in Practice
Ternary Search Trees (TSTs) offer balanced memory usage and faster average lookup times in sparse datasets due to their binary search-like node traversal, while Tries provide consistent O(m) lookup time, where m is the key length, optimized for dense and large alphabets. In practice, Tries generally outperform TSTs in scenarios demanding rapid prefix searches and autocomplete functions because of their direct character indexing, reducing branch comparisons. However, TSTs excel in memory efficiency and handle lexicographical sorting more naturally, making them suitable for applications with limited memory and smaller alphabets.
Implementation Complexity
Ternary Search Trees (TSTs) offer a balanced trade-off between memory usage and implementation complexity compared to Tries, requiring more intricate pointer management due to their ternary node structure with three children per node. Tries implement a straightforward multi-way tree with direct arrays or hash maps representing all possible characters, which simplifies traversal but increases memory consumption and code complexity for large alphabets. Developers often find TST implementation more challenging as it demands careful handling of character comparisons and node transitions, whereas Tries rely heavily on fixed-size or dynamic arrays, impacting scalability and coding effort.
Use Cases and Applications
Ternary Search Trees excel in memory-efficient prefix search, making them ideal for autocomplete systems and spell checkers where space optimization is crucial. Tries offer faster retrieval times and are preferred in IP routing and dictionary implementation where rapid string matching is required. Both data structures support applications in text processing and data compression but differ in trade-offs between speed and space efficiency based on specific use case requirements.
Pros and Cons of TST
Ternary Search Trees (TSTs) offer a space-efficient alternative to Tries by storing characters in nodes with three pointers, reducing memory usage compared to the multiple children pointers in Tries. TSTs provide fast lookups with time complexity close to Tries, especially beneficial for sparse datasets or when the alphabet size is large. However, TSTs tend to have slower worst-case search times than Tries because of the need to traverse nodes sequentially, and their balanced tree structure requires more complex insertion and maintenance algorithms.
Pros and Cons of Trie
Trie data structures excel at prefix-based searches and provide fast retrieval of string data with a time complexity proportional to the key length rather than the number of keys. They require substantial memory due to storing multiple pointers per node, making them less space-efficient compared to Ternary Search Trees. Tries offer straightforward implementation for autocomplete and spell-check functionality but can suffer from increased storage overhead, especially with sparse datasets.
Choosing Between Ternary Search Tree and Trie
Choosing between a Ternary Search Tree (TST) and a Trie depends on the specific use case, especially regarding memory efficiency and search speed. TSTs typically require less memory than Tries, as they store characters in nodes with three pointers and dynamically balance between prefix trees and binary search trees, making them suitable for applications with limited memory. In contrast, Tries offer faster search, insert, and prefix matching operations due to their multi-way branching structure, which is ideal for applications like auto-completion and spell checking where quick lookups on large dictionaries are essential.
Ternary Search Tree Infographic
 libterm.com
libterm.com