The Black-Litterman Model enhances portfolio optimization by combining investor views with market equilibrium returns to generate more stable and diversified asset allocations. This approach helps you manage risk effectively while aligning investments with your market insights. Explore the full article to understand how incorporating the Black-Litterman Model can improve your portfolio strategy.
Table of Comparison
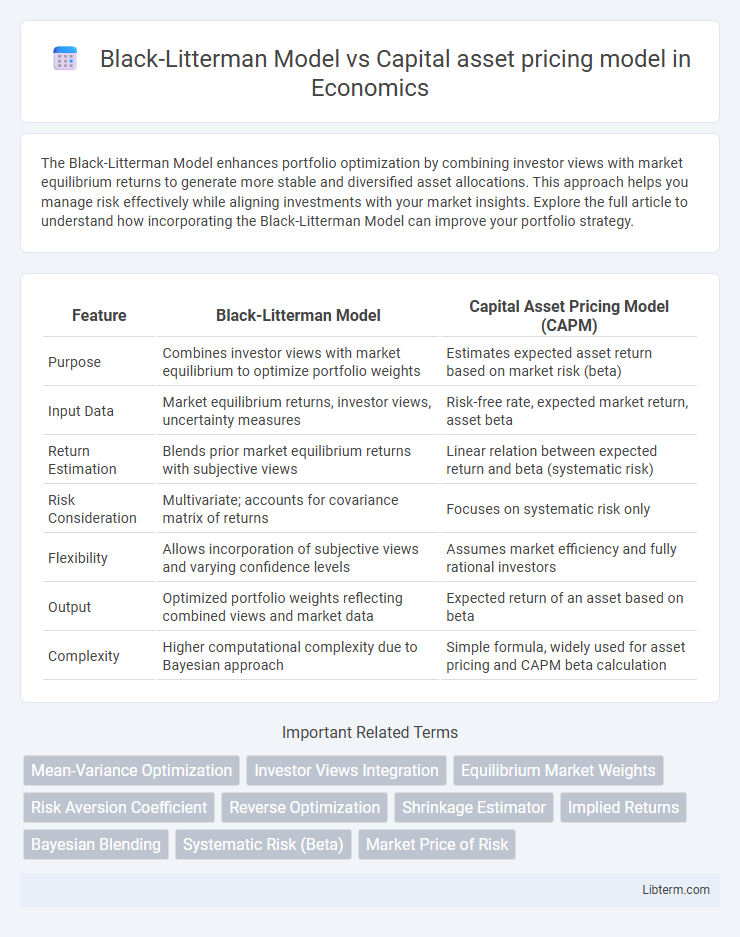
| Feature | Black-Litterman Model | Capital Asset Pricing Model (CAPM) |
|---|---|---|
| Purpose | Combines investor views with market equilibrium to optimize portfolio weights | Estimates expected asset return based on market risk (beta) |
| Input Data | Market equilibrium returns, investor views, uncertainty measures | Risk-free rate, expected market return, asset beta |
| Return Estimation | Blends prior market equilibrium returns with subjective views | Linear relation between expected return and beta (systematic risk) |
| Risk Consideration | Multivariate; accounts for covariance matrix of returns | Focuses on systematic risk only |
| Flexibility | Allows incorporation of subjective views and varying confidence levels | Assumes market efficiency and fully rational investors |
| Output | Optimized portfolio weights reflecting combined views and market data | Expected return of an asset based on beta |
| Complexity | Higher computational complexity due to Bayesian approach | Simple formula, widely used for asset pricing and CAPM beta calculation |
Introduction to Investment Models
The Black-Litterman Model enhances traditional investment strategies by integrating investor views with market equilibrium returns, providing a more flexible asset allocation framework. The Capital Asset Pricing Model (CAPM) fundamentally estimates expected returns based on systematic risk, measured by beta, assuming market efficiency and a single-factor risk. Both models serve as foundational tools in portfolio optimization and risk assessment, yet Black-Litterman addresses the limitations of CAPM by incorporating subjective insights to refine expected returns.
Overview of the Capital Asset Pricing Model (CAPM)
The Capital Asset Pricing Model (CAPM) provides a framework for assessing the expected return of an asset based on its systematic risk measured by beta relative to the overall market. It assumes a linear relationship between expected return and market risk, where the risk-free rate, the asset's beta, and the market risk premium drive the asset's expected performance. CAPM is widely used for portfolio optimization and cost of equity estimation but faces criticism for relying on simplifying assumptions such as market efficiency and a single-factor risk model.
Fundamentals of the Black-Litterman Model
The Black-Litterman Model integrates investor views with market equilibrium implied by the Capital Asset Pricing Model (CAPM) to generate optimal portfolio weights. It enhances portfolio construction by combining the equilibrium excess returns from CAPM with subjective views, adjusting the expected returns through a Bayesian framework. This fundamentally reduces estimation errors and improves diversification by balancing prior market information and individual insights.
Key Assumptions of CAPM vs Black-Litterman
The Capital Asset Pricing Model (CAPM) assumes markets are efficient, investors hold diversified portfolios, and asset returns follow a normal distribution with a linear relationship between risk and expected return based on beta. The Black-Litterman Model integrates investor views with market equilibrium, assuming prior market returns are normally distributed and adjusts asset allocation by blending subjective views with equilibrium market weights. While CAPM relies on simplifying assumptions like a single-period horizon and homogeneous investor expectations, Black-Litterman accommodates multiple views and uncertainty in these views, enhancing portfolio optimization flexibility.
Portfolio Allocation: CAPM Approach
The Capital Asset Pricing Model (CAPM) guides portfolio allocation by quantifying the expected return of an asset based on its systematic risk, measured by beta, relative to the market portfolio. CAPM assumes investors hold diversified portfolios, optimizing the trade-off between expected return and risk, leading to the selection of assets on the efficient frontier. This approach simplifies portfolio construction by relying on market equilibrium assumptions, focusing on market risk premiums without incorporating subjective views or additional information.
Incorporating Investor Views: The Black-Litterman Edge
The Black-Litterman model enhances portfolio optimization by seamlessly integrating subjective investor views with market equilibrium returns, offering a more flexible and intuitive framework compared to the Capital Asset Pricing Model (CAPM). Unlike CAPM, which relies heavily on the assumption of market efficiency and risk premia determined by beta, Black-Litterman adjusts expected returns by blending investor insights with Bayesian statistics, reducing estimation errors and improving portfolio allocation precision. This incorporation of investor views makes Black-Litterman particularly valuable for constructing diversified portfolios that align with specific beliefs and market conditions.
Mathematical Differences: CAPM vs Black-Litterman
The Capital Asset Pricing Model (CAPM) calculates expected asset returns using a linear relationship between an asset's beta and the market return, relying on the formula: \( E(R_i) = R_f + \beta_i (E(R_m) - R_f) \). The Black-Litterman Model integrates CAPM's equilibrium returns as priors and combines them with investor views through Bayesian optimization, resulting in a posterior expected return vector that adjusts the implied equilibrium weights. Unlike CAPM's single-factor approach, Black-Litterman mathematically balances market equilibrium and subjective views by modifying the covariance matrix and incorporating uncertainty in these views, leading to optimized portfolio weights.
Practical Applications in Portfolio Management
The Black-Litterman Model enhances portfolio management by integrating investor views with market equilibrium returns, overcoming CAPM's limitations in practical settings where expected returns are uncertain. Unlike the Capital Asset Pricing Model, which relies on a single factor of market risk (beta) to estimate expected returns, the Black-Litterman approach provides more flexible and tailored asset allocation by combining subjective views with the market consensus. This results in more stable and diversified portfolios, improving risk-adjusted performance in real-world portfolio construction and optimization.
Advantages and Limitations of Each Model
The Black-Litterman Model offers enhanced portfolio optimization by integrating investor views with market equilibrium, reducing estimation errors common in mean-variance optimization, but it requires subjective input that can introduce bias. The Capital Asset Pricing Model (CAPM) provides a straightforward approach to estimating expected returns based on systematic risk (beta), facilitating cost of capital calculations, yet it relies on assumptions like market efficiency and a single risk factor, limiting its predictive accuracy. While Black-Litterman improves allocation stability in complex portfolios, CAPM remains widely used for its simplicity despite oversimplified risk representation.
Choosing the Right Model for Optimal Asset Allocation
The Black-Litterman Model combines investor views with market equilibrium to provide more stable and intuitive optimal asset allocations compared to the Capital Asset Pricing Model (CAPM), which relies heavily on expected returns and market betas. Investors seeking to integrate subjective views and mitigate estimation errors often prefer the Black-Litterman Model for its enhanced portfolio diversification and improved risk-return trade-offs. In contrast, CAPM remains a foundational tool for estimating expected returns based solely on systematic risk, making it suitable for simpler, more theoretical asset allocation frameworks.
Black-Litterman Model Infographic
 libterm.com
libterm.com