A linear production function represents the relationship between inputs and output where the output changes at a constant rate as inputs vary. This function simplifies analysis by assuming constant marginal returns, making it easier to predict production efficiency. Explore the rest of the article to understand how this function impacts your business decisions.
Table of Comparison
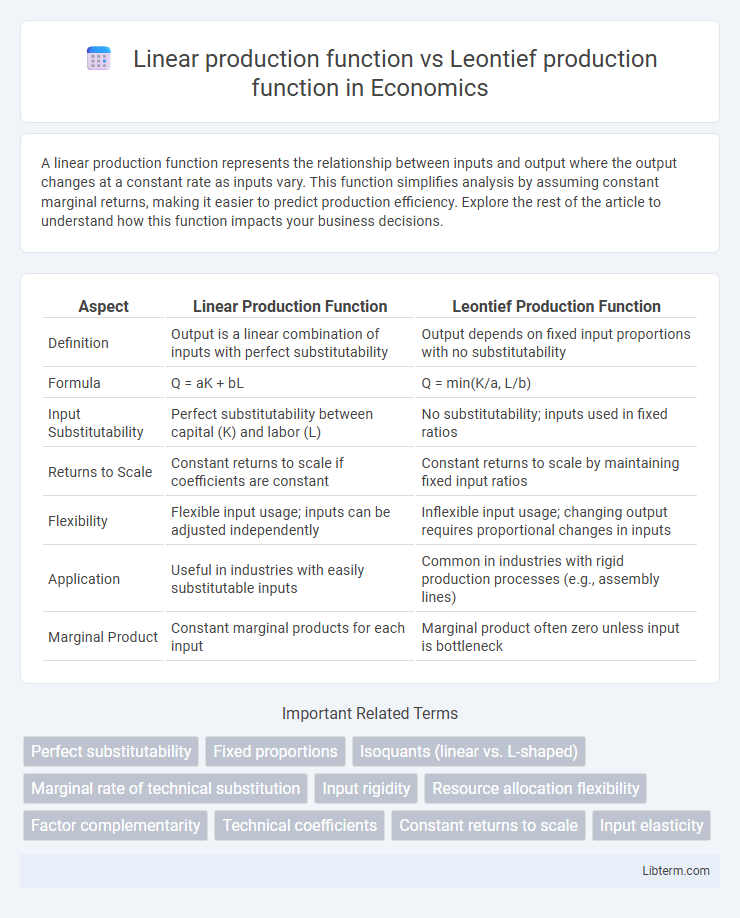
| Aspect | Linear Production Function | Leontief Production Function |
|---|---|---|
| Definition | Output is a linear combination of inputs with perfect substitutability | Output depends on fixed input proportions with no substitutability |
| Formula | Q = aK + bL | Q = min(K/a, L/b) |
| Input Substitutability | Perfect substitutability between capital (K) and labor (L) | No substitutability; inputs used in fixed ratios |
| Returns to Scale | Constant returns to scale if coefficients are constant | Constant returns to scale by maintaining fixed input ratios |
| Flexibility | Flexible input usage; inputs can be adjusted independently | Inflexible input usage; changing output requires proportional changes in inputs |
| Application | Useful in industries with easily substitutable inputs | Common in industries with rigid production processes (e.g., assembly lines) |
| Marginal Product | Constant marginal products for each input | Marginal product often zero unless input is bottleneck |
Introduction to Production Functions
Linear production functions represent output as a constant returns to scale relationship where inputs are perfect substitutes, allowing proportional increases in inputs to result in proportional increases in output. Leontief production functions describe fixed input proportions with no substitution possibilities, meaning output is limited by the minimum input quantity. Understanding these functions is essential in modeling production processes and optimizing resource allocation in economic analysis.
Defining Linear Production Function
The Linear Production Function represents output as a constant proportionate combination of inputs, typically expressed as Q = aK + bL, where Q is output, K is capital, L is labor, and a, b are input coefficients. This function assumes perfect substitutability between inputs, allowing one input to compensate entirely for a reduction in the other without affecting output levels. In contrast, the Leontief Production Function features fixed input proportions, where output is limited by the minimum quantity of any input, reflecting no substitutability between factors.
Defining Leontief Production Function
The Leontief production function represents output as the minimum of weighted input quantities, emphasizing perfect complementarity and fixed input proportions. Unlike the linear production function, which allows substitutability between inputs with constant marginal rates of substitution, the Leontief model assumes no input substitution and strict input combinations. This function is often expressed as \( Q = \min \left(\frac{x_1}{a_1}, \frac{x_2}{a_2}, \ldots, \frac{x_n}{a_n}\right) \), where \( a_i \) are fixed input coefficients reflecting required input ratios.
Mathematical Representation of Linear vs Leontief Functions
The Linear production function is mathematically expressed as Q = a1X1 + a2X2 + ... + anXn, where Q is output, X1 to Xn are inputs, and a1 to an are positive constants representing marginal products. The Leontief production function is represented as Q = min(X1/a1, X2/a2, ..., Xn/an), indicating fixed input proportions where output is limited by the smallest scaled input. Linear functions assume perfect substitutability of inputs, while Leontief functions model inputs as perfect complements, reflecting no substitutability.
Assumptions Underlying Linear and Leontief Models
The Linear production function assumes perfect substitutability between inputs, allowing for smooth substitution without affecting output levels, and constant returns to scale with proportional input increases. In contrast, the Leontief production function relies on fixed input proportions, implying zero substitutability and rigid input requirements to produce output, reflecting a fixed-coefficient technology. These fundamental assumptions cause the Linear model to accommodate flexible input mixes while the Leontief model enforces strict input combinations, impacting production efficiency and input allocation decisions.
Input Substitutability: A Comparative Analysis
The Linear production function allows perfect substitutability between inputs, meaning one input can be increased while another is decreased without affecting output levels. In contrast, the Leontief production function features fixed input proportions, prohibiting any substitutability, as output depends on the minimum quantity of all inputs. This fundamental difference shapes their applicability, with Linear functions suitable for scenarios demanding flexibility in input combinations and Leontief functions modeling rigid, fixed-coefficient processes.
Graphical Illustration: Isoquants of Linear and Leontief Functions
Isoquants of the linear production function are straight lines reflecting perfect substitutability between inputs, illustrating that one input can be substituted for another at a constant rate without changing output. In contrast, the Leontief production function features L-shaped isoquants representing fixed input proportions, where output is limited by the smallest input quantity. These graphical differences highlight how linear functions allow for flexible input combinations, while Leontief functions impose strict input ratios for production efficiency.
Real-World Applications of Linear Production Functions
Linear production functions model output as a direct, proportional combination of inputs, making them highly applicable in industries like manufacturing and agriculture where inputs can be substituted easily. These functions facilitate simple optimization in resource allocation and cost management, enabling firms to predict changes in output when adjusting labor or capital. Real-world applications include assembly lines and crop production, where increasing input quantities consistently boosts output without fixed input ratios.
Real-World Applications of Leontief Production Functions
Leontief production functions are widely used in input-output analysis to model fixed-proportion technologies where inputs must be used in strict ratios, such as in manufacturing processes with assembly lines or chemical production requiring precise reactant quantities. These functions help policymakers and economists analyze inter-industry relationships and forecast economic impacts of changes in demand or supply constraints. Unlike linear production functions that assume perfect substitutability of inputs, Leontief functions provide more realistic insights into industries dependent on rigid input combinations.
Key Differences and Economic Implications
The Linear production function assumes perfect substitutability between inputs, allowing producers to easily trade one input for another with constant returns to scale, while the Leontief production function models fixed input proportions with no substitutability, reflecting rigid technology constraints. Economic implications include flexibility and ease of input adjustment in the Linear model, enabling cost minimization and efficient scaling, whereas the Leontief model enforces strict input ratios, causing potential inefficiencies and limited responsiveness to input price changes. These differences critically impact production planning, cost structures, and resource allocation strategies in various industries.
Linear production function Infographic
 libterm.com
libterm.com