Risk-neutral probability is a fundamental concept in financial mathematics used to price derivatives by assuming investors are indifferent to risk. It transforms real-world probabilities into a "risk-neutral" measure, allowing for simplified valuation of future uncertain payoffs by discounting at the risk-free rate. Explore the rest of this article to understand how risk-neutral probabilities underpin modern pricing models and impact your investment decisions.
Table of Comparison
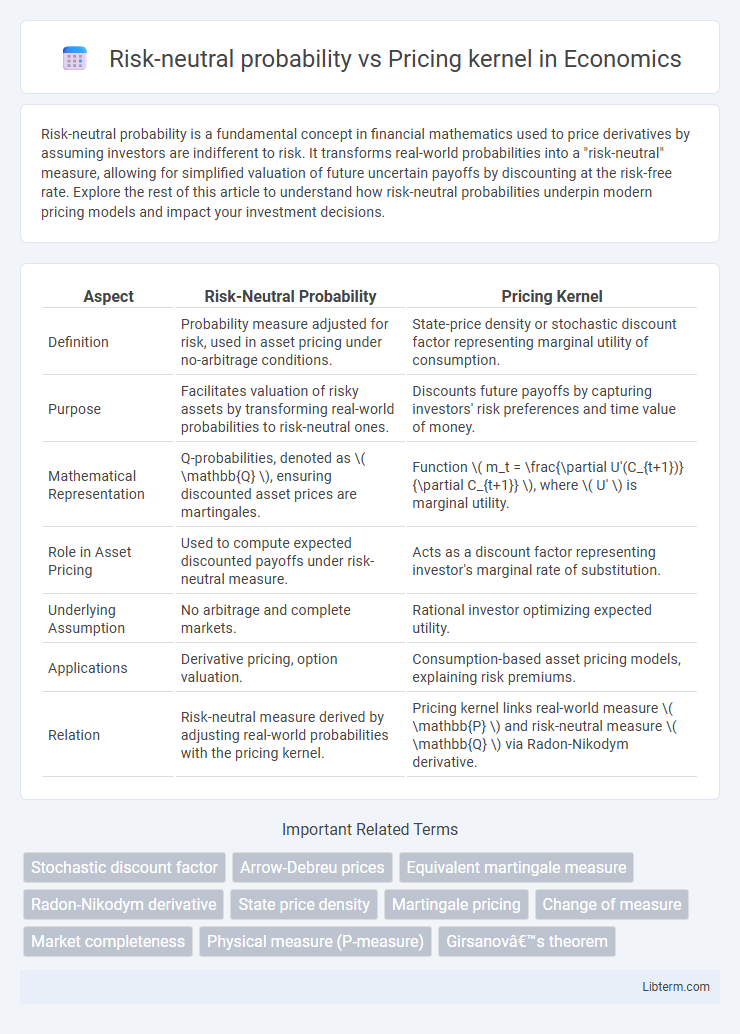
| Aspect | Risk-Neutral Probability | Pricing Kernel |
|---|---|---|
| Definition | Probability measure adjusted for risk, used in asset pricing under no-arbitrage conditions. | State-price density or stochastic discount factor representing marginal utility of consumption. |
| Purpose | Facilitates valuation of risky assets by transforming real-world probabilities to risk-neutral ones. | Discounts future payoffs by capturing investors' risk preferences and time value of money. |
| Mathematical Representation | Q-probabilities, denoted as \( \mathbb{Q} \), ensuring discounted asset prices are martingales. | Function \( m_t = \frac{\partial U'(C_{t+1})}{\partial C_{t+1}} \), where \( U' \) is marginal utility. |
| Role in Asset Pricing | Used to compute expected discounted payoffs under risk-neutral measure. | Acts as a discount factor representing investor's marginal rate of substitution. |
| Underlying Assumption | No arbitrage and complete markets. | Rational investor optimizing expected utility. |
| Applications | Derivative pricing, option valuation. | Consumption-based asset pricing models, explaining risk premiums. |
| Relation | Risk-neutral measure derived by adjusting real-world probabilities with the pricing kernel. | Pricing kernel links real-world measure \( \mathbb{P} \) and risk-neutral measure \( \mathbb{Q} \) via Radon-Nikodym derivative. |
Introduction to Risk-Neutral Probability and Pricing Kernel
Risk-neutral probability is a fundamental concept in financial mathematics that simplifies asset pricing by assuming investors are indifferent to risk, allowing expected payoffs to be discounted at the risk-free rate. The pricing kernel, also known as the stochastic discount factor, represents the state-price density reflecting investors' preferences and risk aversion in valuing uncertain future cash flows. Understanding the relationship between risk-neutral probability and the pricing kernel enables precise modeling of derivative prices and risk adjustments in incomplete markets.
Fundamental Concepts in Financial Derivatives Pricing
Risk-neutral probability facilitates the valuation of financial derivatives by adjusting the real-world probabilities to a "risk-neutral" measure, enabling the expected discounted payoff to equal the current asset price under no arbitrage conditions. The pricing kernel, also known as the stochastic discount factor, links state prices to physical probabilities by adjusting for risk preferences and time value, serving as the fundamental tool to convert future payoffs into present values. Both concepts are crucial in derivative pricing frameworks, with risk-neutral probabilities simplifying calculations in the risk-neutral world, while pricing kernels provide a more general approach incorporating investor risk aversion.
Defining Risk-Neutral Probability
Risk-neutral probability is a theoretical construct used in financial mathematics to price derivatives by assuming all investors are indifferent to risk, allowing expected asset returns to equal the risk-free rate. It transforms the real-world probability measure into a risk-neutral measure, simplifying the valuation of options and other contingent claims. The pricing kernel, also known as the stochastic discount factor, adjusts future payoffs for risk preferences, linking the real-world and risk-neutral probabilities through state-price densities.
Understanding the Pricing Kernel (Stochastic Discount Factor)
The pricing kernel, also known as the stochastic discount factor, represents the state-price density used to value uncertain future cash flows by adjusting for time and risk preferences in asset pricing models. Unlike risk-neutral probability, which modifies probabilities to reflect risk-adjusted expectations under a hypothetical risk-neutral measure, the pricing kernel directly discounts payoffs using the marginal utility of consumption or consumption equivalents. Understanding the pricing kernel is essential for linking asset prices to fundamental economic variables, as it captures both time value and risk aversion embedded in market prices.
Mathematical Formulation: Risk-Neutral Measure
Risk-neutral probability measures transform the real-world probability space to a risk-adjusted one where discounted asset prices become martingales, enabling simpler derivative pricing under the risk-neutral measure \( \mathbb{Q} \). The pricing kernel, or stochastic discount factor \( m_t \), relates the physical measure \( \mathbb{P} \) to the risk-neutral measure through Radon-Nikodym derivatives, expressed mathematically as \( \frac{d\mathbb{Q}}{d\mathbb{P}} = m_t / \mathbb{E}[m_t] \). This connection ensures that the expected value of future payoffs discounted by \( m_t \) equals current asset prices, formalizing the no-arbitrage condition within the mathematical framework of asset pricing.
Mathematical Formulation: Pricing Kernel Approach
The pricing kernel approach in mathematical finance represents state prices as the product of a stochastic discount factor and the payoff of an asset, expressed as \( \pi_t = m_t X_t \), where \( m_t \) is the pricing kernel or stochastic discount factor. This formulation relates expected payoffs under the real-world probability measure \( \mathbb{P} \) discounted by the pricing kernel, i.e., the asset price \( S_t = \mathbb{E}^{\mathbb{P}}[m_T X_T | \mathcal{F}_t] \). Unlike risk-neutral probabilities that adjust measures to price assets by discounting at the risk-free rate, the pricing kernel directly incorporates investor preferences and risk aversion through its structure, making it a fundamental tool in equilibrium asset pricing models.
Relationship Between Risk-Neutral Probability and Pricing Kernel
The relationship between risk-neutral probability and pricing kernel is fundamental in asset pricing, where the pricing kernel acts as a stochastic discount factor that adjusts real-world probabilities to risk-neutral probabilities for valuation. Risk-neutral probabilities emerge by weighting the real-world probabilities with the pricing kernel, effectively reflecting investors' risk preferences and market prices of risk. This transformation enables the calculation of fair asset prices under the risk-neutral measure, simplifying the modeling of expected payoffs discounted at the risk-free rate.
Practical Applications in Asset Pricing
Risk-neutral probability simplifies asset pricing by adjusting real-world probabilities to reflect investors' risk preferences, enabling straightforward calculation of expected payoffs discounted at the risk-free rate. The pricing kernel, or stochastic discount factor, directly incorporates investor risk aversion and intertemporal consumption preferences, providing a more comprehensive framework for valuing assets under uncertainty. Practical applications include option pricing models, such as the Black-Scholes formula using risk-neutral probabilities, and consumption-based capital asset pricing models (CAPM) employing the pricing kernel to explain asset returns in equilibrium.
Advantages and Limitations of Each Approach
Risk-neutral probability simplifies asset pricing by assuming investors are indifferent to risk, enabling straightforward discounting of expected payoffs with the risk-free rate, which facilitates easier computational models but may overlook actual market risk preferences. Pricing kernel incorporates investors' risk aversion and consumption preferences, providing a more realistic and comprehensive framework for asset valuation, yet it involves complex estimation and calibration challenges. Risk-neutral probability excels in practical implementation and model tractability, while pricing kernel offers nuanced insights at the cost of increased mathematical and empirical complexity.
Conclusion: Choosing Between Risk-Neutral Probability and Pricing Kernel
Choosing between risk-neutral probability and pricing kernel depends on the analytical framework and purpose; risk-neutral probability simplifies asset pricing by adjusting probabilities to discount expected payoffs at the risk-free rate, ideal for derivative pricing and arbitrage arguments. The pricing kernel incorporates investors' risk preferences and marginal utility changes, providing richer insights into risk premia and equilibrium asset pricing models. Selecting the appropriate tool aligns with whether the focus is on computational convenience or a deeper understanding of risk adjustments in market equilibrium.
Risk-neutral probability Infographic
 libterm.com
libterm.com