Bayesian Nash equilibrium represents a strategic balance in games with incomplete information, where each player's strategy maximizes their expected payoff given beliefs about other players' types. This concept extends the classical Nash equilibrium by incorporating probabilistic reasoning, allowing players to update their expectations based on available information. Explore the rest of the article to understand how Bayesian Nash equilibrium applies to real-world strategic decision-making scenarios.
Table of Comparison
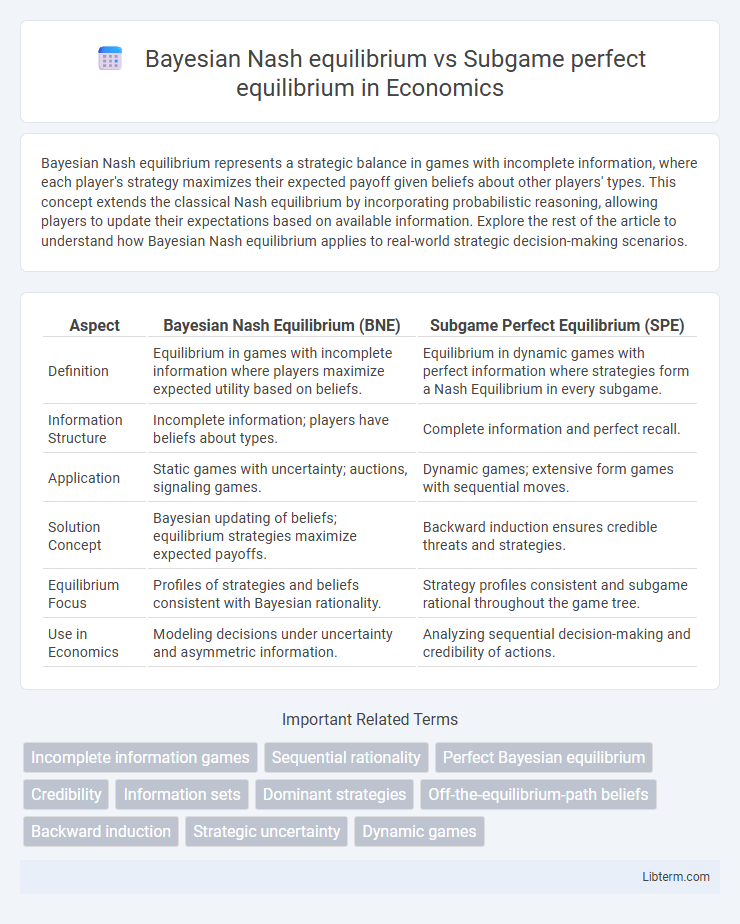
| Aspect | Bayesian Nash Equilibrium (BNE) | Subgame Perfect Equilibrium (SPE) |
|---|---|---|
| Definition | Equilibrium in games with incomplete information where players maximize expected utility based on beliefs. | Equilibrium in dynamic games with perfect information where strategies form a Nash Equilibrium in every subgame. |
| Information Structure | Incomplete information; players have beliefs about types. | Complete information and perfect recall. |
| Application | Static games with uncertainty; auctions, signaling games. | Dynamic games; extensive form games with sequential moves. |
| Solution Concept | Bayesian updating of beliefs; equilibrium strategies maximize expected payoffs. | Backward induction ensures credible threats and strategies. |
| Equilibrium Focus | Profiles of strategies and beliefs consistent with Bayesian rationality. | Strategy profiles consistent and subgame rational throughout the game tree. |
| Use in Economics | Modeling decisions under uncertainty and asymmetric information. | Analyzing sequential decision-making and credibility of actions. |
Introduction to Game Theory Equilibriums
Bayesian Nash equilibrium refines the Nash equilibrium by incorporating incomplete information, where players hold beliefs about unknown types and choose strategies maximizing expected utility based on these beliefs. Subgame perfect equilibrium strengthens Nash equilibrium by requiring strategies to form a Nash equilibrium in every subgame, ensuring credibility of threats and promises in dynamic games. Both equilibria address strategic stability, with Bayesian Nash equilibrium applying to games of incomplete information and subgame perfect equilibrium focusing on sequential rationality in extensive-form games.
Understanding Bayesian Nash Equilibrium
Bayesian Nash equilibrium extends the concept of Nash equilibrium to games with incomplete information, where players have beliefs about unknown parameters represented by probability distributions. It requires each player's strategy to be a best response given their beliefs about other players' types and strategies, incorporating Bayesian updating. This equilibrium concept is essential for analyzing strategic interactions in games where players possess private information.
Defining Subgame Perfect Equilibrium
Subgame Perfect Equilibrium (SPE) refines Nash equilibrium by requiring strategies to constitute a Nash equilibrium in every subgame of the original game, ensuring credibility and consistency in dynamic games. Unlike Bayesian Nash equilibrium, which accounts for incomplete information and player beliefs, SPE applies mainly to extensive-form games with perfect information or observed histories. SPE eliminates non-credible threats by enforcing sequential rationality at every decision node within the game tree, making it essential for analyzing multi-stage strategic interactions.
Key Differences Between the Two Equilibriums
Bayesian Nash equilibrium incorporates players' beliefs about other players' types in games with incomplete information, ensuring strategies are optimal given these beliefs. In contrast, Subgame perfect equilibrium applies to dynamic games with perfect information, requiring strategies to constitute a Nash equilibrium in every subgame, thus eliminating non-credible threats. The key difference lies in Bayesian Nash equilibrium addressing uncertainty through probabilistic beliefs, while Subgame perfect equilibrium enforces sequential rationality throughout all stages of the game.
Information Structure: Complete vs Incomplete Information
Bayesian Nash equilibrium applies to games with incomplete information where players have beliefs about other players' types, represented by probability distributions, reflecting uncertainty in the information structure. Subgame perfect equilibrium is used in games with complete information, ensuring credible strategies in every subgame by solving the game through backward induction. The key distinction lies in Bayesian Nash equilibrium accommodating private information and uncertainty, while subgame perfect equilibrium requires full knowledge of payoffs and strategies throughout the game.
Strategic Form Games vs Extensive Form Games
Bayesian Nash equilibrium applies primarily in strategic form games with incomplete information, where players hold beliefs about other players' types and choose strategies maximizing expected utility given those beliefs. Subgame perfect equilibrium is defined in extensive form games, ensuring that players' strategies constitute a Nash equilibrium in every subgame, thereby refining strategic form equilibria by accounting for the sequential structure of decisions. Strategic form games capture simultaneous moves without temporal order, while extensive form games represent dynamic interactions with explicit timing and observed actions, necessitating subgame perfect equilibrium concepts for credible threats and promises.
Example Scenarios Applying Bayesian Nash Equilibrium
Bayesian Nash equilibrium applies to games with incomplete information, where players have beliefs about others' types, such as bidding in auctions or signaling in market entry games. In contrast, subgame perfect equilibrium is used in dynamic games with perfect information, ensuring credible strategies in every subgame, like sequential bargaining or ultimatum games. Auction scenarios, such as first-price sealed-bid auctions, demonstrate Bayesian Nash equilibrium by modeling bidders' strategies based on their private valuations and beliefs about opponents' valuations.
Example Scenarios Utilizing Subgame Perfect Equilibrium
Subgame Perfect Equilibrium (SPE) refines Nash Equilibrium by ensuring strategies form a Nash Equilibrium in every subgame, making it crucial in sequential games such as bargaining or entry deterrence models. For instance, in the ultimatum game, SPE predicts the responder's acceptance threshold at every possible offer stage, guiding the proposer's optimal offer precisely. This contrasts with Bayesian Nash Equilibrium, which incorporates incomplete information and player beliefs, often applied in auction models or signaling games where private information impacts strategy formulation.
Practical Implications in Economics and Strategy
Bayesian Nash equilibrium applies to games with incomplete information, allowing firms or players to form strategies based on beliefs about others' types, making it crucial in auctions and contract design where private information affects outcomes. Subgame perfect equilibrium ensures credible strategies in dynamic games with sequential moves, fostering consistency in decision-making at every stage, which is vital for modeling negotiations, bargaining, and multi-stage investment decisions. Understanding these equilibria helps economists and strategists design mechanisms and predict stable outcomes under uncertainty and strategic foresight.
Summary and Choosing the Appropriate Equilibrium
Bayesian Nash equilibrium applies to games with incomplete information, where players hold beliefs about others' types and choose strategies maximizing expected utility based on these beliefs. Subgame perfect equilibrium refines Nash equilibrium by requiring strategies to form a Nash equilibrium in every subgame, ensuring credible and consistent planning in dynamic games with perfect information. Choosing the appropriate equilibrium depends on the game's structure: Bayesian Nash equilibrium suits games with private information, while subgame perfect equilibrium fits sequential games where credible commitment at every stage is crucial.
Bayesian Nash equilibrium Infographic
 libterm.com
libterm.com