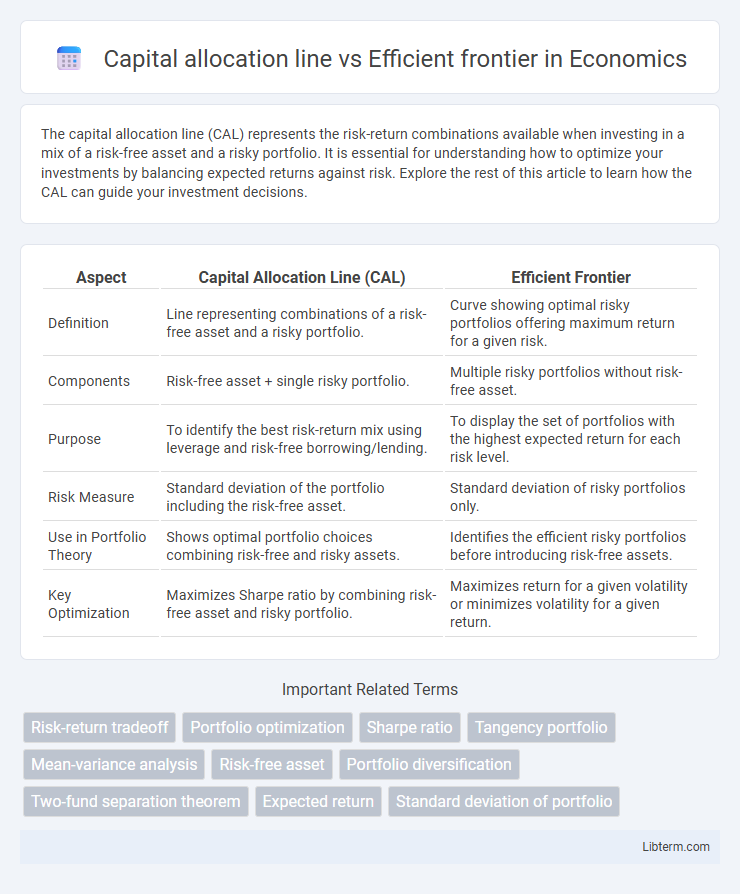
The capital allocation line (CAL) represents the risk-return combinations available when investing in a mix of a risk-free asset and a risky portfolio. It is essential for understanding how to optimize your investments by balancing expected returns against risk. Explore the rest of this article to learn how the CAL can guide your investment decisions.
Table of Comparison
| Aspect | Capital Allocation Line (CAL) | Efficient Frontier |
|---|---|---|
| Definition | Line representing combinations of a risk-free asset and a risky portfolio. | Curve showing optimal risky portfolios offering maximum return for a given risk. |
| Components | Risk-free asset + single risky portfolio. | Multiple risky portfolios without risk-free asset. |
| Purpose | To identify the best risk-return mix using leverage and risk-free borrowing/lending. | To display the set of portfolios with the highest expected return for each risk level. |
| Risk Measure | Standard deviation of the portfolio including the risk-free asset. | Standard deviation of risky portfolios only. |
| Use in Portfolio Theory | Shows optimal portfolio choices combining risk-free and risky assets. | Identifies the efficient risky portfolios before introducing risk-free assets. |
| Key Optimization | Maximizes Sharpe ratio by combining risk-free asset and risky portfolio. | Maximizes return for a given volatility or minimizes volatility for a given return. |
Introduction to Capital Allocation Line and Efficient Frontier
The Capital Allocation Line (CAL) represents the risk-return combinations available to investors by mixing a risk-free asset with a portfolio of risky assets, illustrating the trade-off between expected return and risk. The Efficient Frontier is a curve depicting the set of optimal portfolios offering the maximum expected return for a given level of risk, derived from Modern Portfolio Theory. Understanding the relationship between the CAL and the Efficient Frontier helps investors identify the best feasible portfolio that maximizes returns while managing risk.
Key Concepts: Risk, Return, and Diversification
The Capital Allocation Line (CAL) represents the risk-return trade-off for a combination of a risk-free asset and a risky portfolio, illustrating how investors can optimize expected return for a given level of risk through diversification. The Efficient Frontier consists of portfolios that offer the highest expected return for each level of risk, highlighting the optimal trade-off between risk and return without a risk-free asset. Both concepts emphasize diversification's role in minimizing risk while maximizing returns, with the CAL incorporating risk-free assets to further enhance portfolio efficiency.
What is the Capital Allocation Line (CAL)?
The Capital Allocation Line (CAL) represents all possible combinations of a risk-free asset and a risky portfolio, displaying the highest expected return for each level of risk. It originates at the risk-free rate on the y-axis and is tangent to the efficient frontier, which illustrates the set of optimal risky portfolios offering the maximum return for a given risk. The slope of the CAL, known as the Sharpe ratio, measures the risk-adjusted return and guides investors in choosing the best mix of risk-free and risky assets.
Understanding the Efficient Frontier
The Efficient Frontier represents the set of optimal portfolios that offer the highest expected return for a given level of risk, based on Modern Portfolio Theory. It is derived by plotting portfolios that maximize expected return while minimizing variance, highlighting the trade-off between risk and return. Understanding the Efficient Frontier enables investors to select portfolios that align with their risk tolerance, unlike the Capital Allocation Line which illustrates combinations of a risk-free asset and a risky portfolio.
CAL vs. Efficient Frontier: Fundamental Differences
The Capital Allocation Line (CAL) represents portfolios combining a risk-free asset with a risky portfolio, illustrating risk-return trade-offs for a given investor's risk tolerance. The Efficient Frontier, derived from Markowitz's Modern Portfolio Theory, depicts the set of optimal risky portfolios that offer the highest expected return for a specific level of risk. Unlike the CAL, which includes a risk-free asset and focuses on investor preferences, the Efficient Frontier exclusively considers combinations of risky assets, emphasizing portfolio optimization without risk-free borrowing or lending.
Role of the Risk-Free Asset in Portfolio Construction
The Capital Allocation Line (CAL) represents combinations of a risk-free asset and a risky portfolio, highlighting the optimal risk-return trade-off by incorporating the risk-free rate into portfolio construction. In contrast, the Efficient Frontier comprises portfolios of risky assets that offer the highest expected return for a given level of risk, excluding the risk-free asset. The inclusion of the risk-free asset in the CAL allows investors to achieve better diversification and leverage by combining it with the efficient risky portfolio, thus shifting the investment opportunity set beyond the Efficient Frontier.
Investor Preferences: Utility and Indifference Curves
Investor preferences are crucial in differentiating the Capital Allocation Line (CAL) from the Efficient Frontier by incorporating utility and indifference curves. The CAL represents combinations of a risk-free asset and a risky portfolio, aligning with investor utility maximization based on their risk tolerance. Indifference curves illustrate investor satisfaction levels, allowing for the selection of an optimal portfolio on the CAL that maximizes expected utility beyond the efficient frontier's risk-return trade-offs.
Optimal Portfolio Selection: Where CAL Meets Efficient Frontier
The Capital Allocation Line (CAL) represents portfolios combining a risk-free asset with a risky portfolio, showing the best risk-return trade-offs for different levels of risk. The Efficient Frontier illustrates the set of optimal risky portfolios offering the highest expected return for a given level of risk, derived from mean-variance optimization. Optimal portfolio selection occurs at the tangent point where the CAL touches the Efficient Frontier, defining the market portfolio that maximizes the Sharpe ratio and balances risk and return most efficiently.
Practical Applications in Modern Portfolio Theory
The Capital Allocation Line (CAL) represents combinations of risk-free assets and a portfolio of risky assets, guiding investors to achieve optimal risk-return trade-offs through practical leverage and borrowing strategies. The Efficient Frontier, constructed from risky asset portfolios, identifies portfolios offering the highest expected return for a given risk level, serving as a benchmark for asset allocation and diversification in Modern Portfolio Theory. Together, the CAL and Efficient Frontier facilitate dynamic portfolio construction by integrating risk-free rates with efficient risky portfolios, optimizing capital allocation to meet specific investor risk preferences.
Conclusion: Choosing Between CAL and Efficient Frontier
Choosing between the Capital Allocation Line (CAL) and the Efficient Frontier depends on an investor's risk tolerance and investment goals. The CAL represents portfolios combining a risk-free asset with a market portfolio to optimize risk-return trade-offs, ideal for individual investor decisions. The Efficient Frontier showcases the set of optimal portfolios offering the highest expected return for a given level of risk, useful for institutional portfolio construction and diversification strategies.
Capital allocation line Infographic
 libterm.com
libterm.com