Correlated equilibrium is a solution concept in game theory where players coordinate their strategies through signals from a trusted mediator, leading to outcomes potentially better than Nash equilibrium. This concept allows for cooperation without direct communication by aligning incentives and expectations. Explore the rest of the article to understand how correlated equilibrium can impact strategic decision-making in various fields.
Table of Comparison
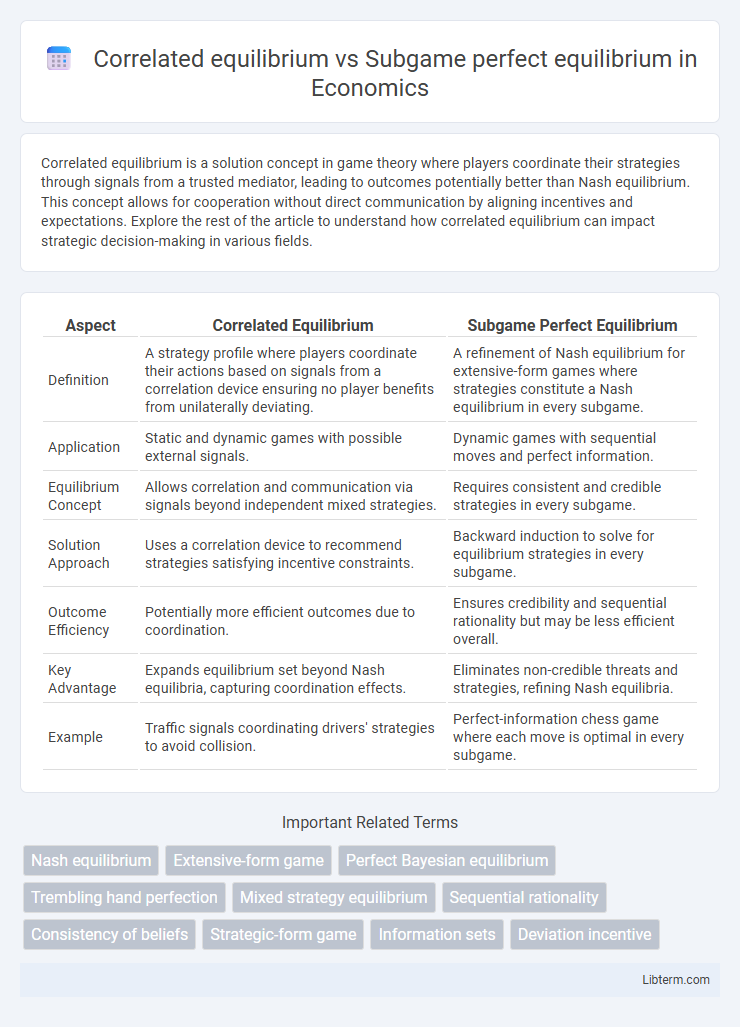
| Aspect | Correlated Equilibrium | Subgame Perfect Equilibrium |
|---|---|---|
| Definition | A strategy profile where players coordinate their actions based on signals from a correlation device ensuring no player benefits from unilaterally deviating. | A refinement of Nash equilibrium for extensive-form games where strategies constitute a Nash equilibrium in every subgame. |
| Application | Static and dynamic games with possible external signals. | Dynamic games with sequential moves and perfect information. |
| Equilibrium Concept | Allows correlation and communication via signals beyond independent mixed strategies. | Requires consistent and credible strategies in every subgame. |
| Solution Approach | Uses a correlation device to recommend strategies satisfying incentive constraints. | Backward induction to solve for equilibrium strategies in every subgame. |
| Outcome Efficiency | Potentially more efficient outcomes due to coordination. | Ensures credibility and sequential rationality but may be less efficient overall. |
| Key Advantage | Expands equilibrium set beyond Nash equilibria, capturing coordination effects. | Eliminates non-credible threats and strategies, refining Nash equilibria. |
| Example | Traffic signals coordinating drivers' strategies to avoid collision. | Perfect-information chess game where each move is optimal in every subgame. |
Introduction to Game Theory Equilibria
Correlated equilibrium extends Nash equilibrium by allowing players to coordinate their strategies through shared signals, leading to potentially higher payoffs and more efficient outcomes in strategic games. Subgame perfect equilibrium refines Nash equilibrium by requiring strategy profiles to constitute a Nash equilibrium in every subgame, ensuring credibility and consistency in dynamic games with sequential moves. Both concepts play crucial roles in game theory equilibria analysis, addressing different aspects of strategic interaction and decision-making processes.
Defining Correlated Equilibrium
Correlated equilibrium extends the concept of Nash equilibrium by allowing players to coordinate their strategies through signals from a correlation device, leading to potentially higher payoffs and more efficient outcomes. Unlike subgame perfect equilibrium, which refines Nash equilibrium by requiring credible strategies in every subgame of a dynamic game, correlated equilibrium captures a broader set of strategy profiles based on shared information and correlation. This equilibrium concept is particularly useful in games where players can condition their actions on external signals, promoting coordinated behavior without direct communication.
Understanding Subgame Perfect Equilibrium
Subgame Perfect Equilibrium (SPE) refines Nash equilibrium by requiring strategy profiles to constitute a Nash equilibrium in every subgame of the original game, ensuring credible threats and promises at every stage. This concept is especially crucial in dynamic games with sequential moves, where players anticipate future actions and adjust strategies accordingly. SPE is identified through backward induction, emphasizing rationality and consistency in every possible continuation of the game, contrasting with Correlated Equilibrium, which allows coordination through correlation devices without sequential rationality constraints.
Key Differences Between Correlated and Subgame Perfect Equilibria
Correlated equilibrium allows players to coordinate their strategies based on signals from an external mediator, enabling correlated strategies that can improve joint payoffs, whereas subgame perfect equilibrium requires players' strategies to constitute a Nash equilibrium in every subgame of a dynamic game, ensuring credible threats and consistent optimal decisions at every stage. Correlated equilibrium generalizes Nash equilibrium and may yield multiple equilibria with coordinated outcomes, while subgame perfect equilibrium refines Nash equilibrium by eliminating non-credible threats in sequential move games. The key difference lies in correlation devices influencing players' strategy choices in correlated equilibrium, contrasting with subgame perfect equilibrium's focus on time-consistent strategies in extensive-form games.
Strategic Implications in Multi-Stage Games
Correlated equilibrium allows players in multi-stage games to coordinate strategies through shared signals, enabling more efficient outcomes compared to independent strategy choices in subgame perfect equilibrium, which enforces sequential rationality at every stage. Strategic implications include enhanced cooperation possibilities in correlated equilibria, reducing the occurrence of non-credible threats that subgame perfect equilibria aim to eliminate through backward induction. This leads to potential welfare improvements in multi-stage interactions when players can commit to or observe correlation devices, expanding the set of achievable equilibria beyond the strict sequential rationality constraints of subgame perfect equilibrium.
Mathematical Formulations and Examples
Correlated equilibrium extends Nash equilibrium by allowing players to condition their strategies on signals received from a public randomizing device, mathematically represented by joint probability distributions over strategy profiles satisfying incentive compatibility constraints for each player. Subgame perfect equilibrium refines Nash equilibrium in dynamic games by requiring strategy profiles to constitute a Nash equilibrium in every subgame, formulated through backward induction and recursive value functions ensuring optimal continuation strategies. An example of correlated equilibrium is the use of a correlating device in a traffic game to reduce collisions, while a subgame perfect equilibrium example is the sequential entry-deterrence game where the incumbent's threat strategy deters market entry by optimizing payoffs at every decision node.
Applications in Economics and Real-World Scenarios
Correlated equilibrium offers a practical framework for modeling coordination among economic agents in markets, enabling improved prediction of outcomes in situations with communication or signaling, such as auction design and traffic flow management. Subgame perfect equilibrium is crucial for dynamic strategic interactions with sequential moves, often applied in bargaining scenarios, regulatory policy formation, and contract theory to ensure credibility and consistency throughout every stage of decision-making. Both solution concepts enhance game-theoretic analysis in economic environments by capturing different strategic complexities--correlated equilibrium addresses correlated strategies and signals, while subgame perfect equilibrium ensures sequential rationality in extensive-form games.
Advantages and Limitations of Each Equilibrium
Correlated equilibrium allows for a broader set of strategies by enabling players to coordinate their actions through signals, leading to potentially higher payoffs and more efficient outcomes than Nash equilibria. Its limitation lies in the assumption that players receive and trust external signals, which may not be feasible in all strategic settings. Subgame perfect equilibrium guarantees credible strategies in every subgame, ensuring consistent optimal play throughout dynamic games, but it can be overly restrictive and may exclude mutually beneficial cooperative solutions achievable through correlation.
Conditions for Existence and Uniqueness
Correlated equilibrium exists under broader conditions because it requires only that players follow signals inducing no profitable deviations, making it guaranteed in finite games with compact, convex strategy spaces. Subgame perfect equilibrium necessitates sequential rationality in every subgame, often ensuring uniqueness in games with perfect information and strictly ordered payoffs due to backward induction. Uniqueness of correlated equilibrium is rare and depends on specific payoff structures, whereas subgame perfect equilibrium tends to be unique when the game's sequential structure and payoffs prevent multiple credible strategy profiles.
Conclusion: Choosing the Appropriate Equilibrium
Selecting between correlated equilibrium and subgame perfect equilibrium depends on the strategic context and information structure of the game. Correlated equilibrium allows for players to coordinate strategies through signals, often leading to more efficient outcomes in games with communication or external correlation devices. Subgame perfect equilibrium is preferred in sequential games to ensure credible strategies at every stage, emphasizing consistency and individual rationality in dynamic decision-making.
Correlated equilibrium Infographic
 libterm.com
libterm.com