The impedance matrix characterizes the relationship between voltages and currents in multi-port electrical networks, capturing how each port influences others. This matrix plays a crucial role in analyzing complex circuits, enabling engineers to predict system behavior and optimize signal flow. Discover how understanding the impedance matrix can enhance your electrical design by exploring the details in the following article.
Table of Comparison
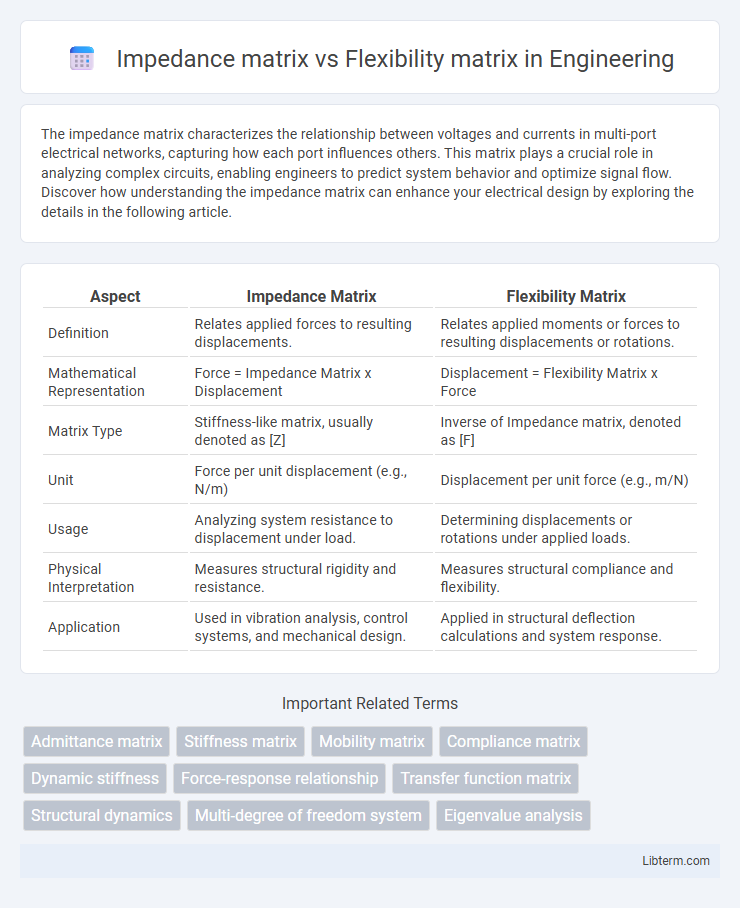
| Aspect | Impedance Matrix | Flexibility Matrix |
|---|---|---|
| Definition | Relates applied forces to resulting displacements. | Relates applied moments or forces to resulting displacements or rotations. |
| Mathematical Representation | Force = Impedance Matrix x Displacement | Displacement = Flexibility Matrix x Force |
| Matrix Type | Stiffness-like matrix, usually denoted as [Z] | Inverse of Impedance matrix, denoted as [F] |
| Unit | Force per unit displacement (e.g., N/m) | Displacement per unit force (e.g., m/N) |
| Usage | Analyzing system resistance to displacement under load. | Determining displacements or rotations under applied loads. |
| Physical Interpretation | Measures structural rigidity and resistance. | Measures structural compliance and flexibility. |
| Application | Used in vibration analysis, control systems, and mechanical design. | Applied in structural deflection calculations and system response. |
Introduction to Structural Matrices
The impedance matrix represents the relationship between applied forces and resulting displacements in structural systems, capturing the system's stiffness characteristics. In contrast, the flexibility matrix expresses displacements as a function of applied forces, emphasizing the system's compliance or deformability. Both matrices are fundamental in structural analysis, enabling engineers to model and predict structural behavior under various loading conditions accurately.
Understanding the Impedance Matrix
The impedance matrix characterizes the relationship between forces and displacements in mechanical systems by relating applied forces to resulting velocities or displacements through frequency-dependent complex values. It is essential in vibration analysis and structural dynamics for predicting system behavior under dynamic loading conditions. Unlike the flexibility matrix, which directly relates displacements to forces, the impedance matrix incorporates inertial, damping, and stiffness effects, providing a comprehensive representation of system dynamics.
Fundamentals of Flexibility Matrix
The flexibility matrix represents the inverse of the stiffness matrix, quantifying the displacement response of a structure under applied loads, while the impedance matrix relates force and velocity in dynamic systems. Fundamentally, the flexibility matrix provides a static relationship by expressing structural deformations as functions of applied forces, making it essential in structural analysis for determining displacements and rotations. It serves as a key tool in understanding the elastic behavior of systems, enabling engineers to model how structures deform under various loading conditions.
Mathematical Formulation
The impedance matrix represents the system's response by relating input forces to resulting velocities through complex frequency-dependent parameters, typically denoted as Z(o), where each element Z_ij quantifies the interaction between the i-th input and j-th output. The flexibility matrix, often represented as F, is the inverse of the stiffness matrix K and defines the displacement response of a structure to applied forces in the time or static domain, with F = K^(-1). Mathematically, the impedance matrix is formulated in the frequency domain as Z = R + joM - (j/o)C, incorporating resistance (R), mass (M), and compliance (C), while the flexibility matrix is purely static or low-frequency, derived by F = [K]^(-1), emphasizing the reciprocal relationship between force and displacement.
Physical Interpretation
The impedance matrix represents the dynamic relationship between applied forces and resulting velocities in mechanical systems, capturing how the structure resists motion under excitation. The flexibility matrix describes the static deformation response of a structure to applied forces, indicating how displacements arise from loads. Physically, impedance matrix quantifies system resistance in the frequency domain, while flexibility matrix quantifies compliance in the static or quasi-static domain.
Applications in Engineering
The impedance matrix is crucial in structural engineering for analyzing stiffness and force distribution in complex systems, enabling precise control of mechanical responses in robotics and aerospace design. The flexibility matrix finds applications in mechanical and civil engineering for evaluating displacement under loads, essential for designing compliant mechanisms and assessing structural deformation. Both matrices complement finite element analysis by optimizing structural performance and ensuring safety in engineering designs.
Comparative Analysis: Impedance vs Flexibility
The impedance matrix, representing system stiffness, relates forces to displacements and is typically symmetric and positive definite, while the flexibility matrix, the inverse of the impedance matrix, expresses displacements as functions of applied forces, capturing system compliance. In structural dynamics, impedance matrices are favored for their ease in handling boundary conditions and compatibility with finite element methods, whereas flexibility matrices are preferred in systems where force inputs are known, facilitating direct computation of displacements. Comparative analysis reveals impedance matrices provide stability and numerical efficiency in simulations, whereas flexibility matrices offer intuitive insights into deformability and are particularly useful in inverse problems and fault diagnosis.
Advantages and Limitations
The impedance matrix offers a direct relationship between forces and displacements in mechanical systems, making it advantageous for analyzing dynamic responses and vibration characteristics with precise frequency-dependent behavior. Its limitation lies in computational complexity for large-scale systems and challenges in handling non-linearities. The flexibility matrix, relating displacements to applied forces, provides intuitive insights into static deflections and structural compliance but may be less effective in capturing dynamic interactions and frequency-dependent phenomena.
Selection Criteria for Practical Problems
The impedance matrix is preferred in practical problems requiring stable solutions for force-driven systems, as it directly relates applied forces to displacements with better numerical conditioning under high stiffness conditions. The flexibility matrix is advantageous in displacement-driven scenarios where direct calculation of displacement responses to applied forces is necessary, especially in systems with low stiffness and when inversion of the impedance matrix may cause instability. Selection criteria revolve around the system's loading type, stiffness characteristics, and computational efficiency, favoring the impedance matrix for force control and the flexibility matrix for displacement control problems.
Future Trends and Research Directions
Emerging research trends emphasize integrating impedance matrix and flexibility matrix analyses to enhance structural health monitoring and smart material design. Advanced computational techniques and machine learning algorithms are driving improved accuracy in predicting system behavior under dynamic loads. Future directions focus on hybrid models combining impedance and flexibility matrices for real-time adaptive control in aerospace and robotics applications.
Impedance matrix Infographic
 libterm.com
libterm.com