General three-dimensional stress refers to the state of stress at a point within a material where forces act in all three spatial directions, characterized by a 3x3 stress tensor containing normal and shear stress components. Understanding this complex stress state is essential for predicting material behavior under multidirectional loading conditions in engineering applications. Explore the rest of the article to deepen your knowledge of how these stresses influence structural integrity and design.
Table of Comparison
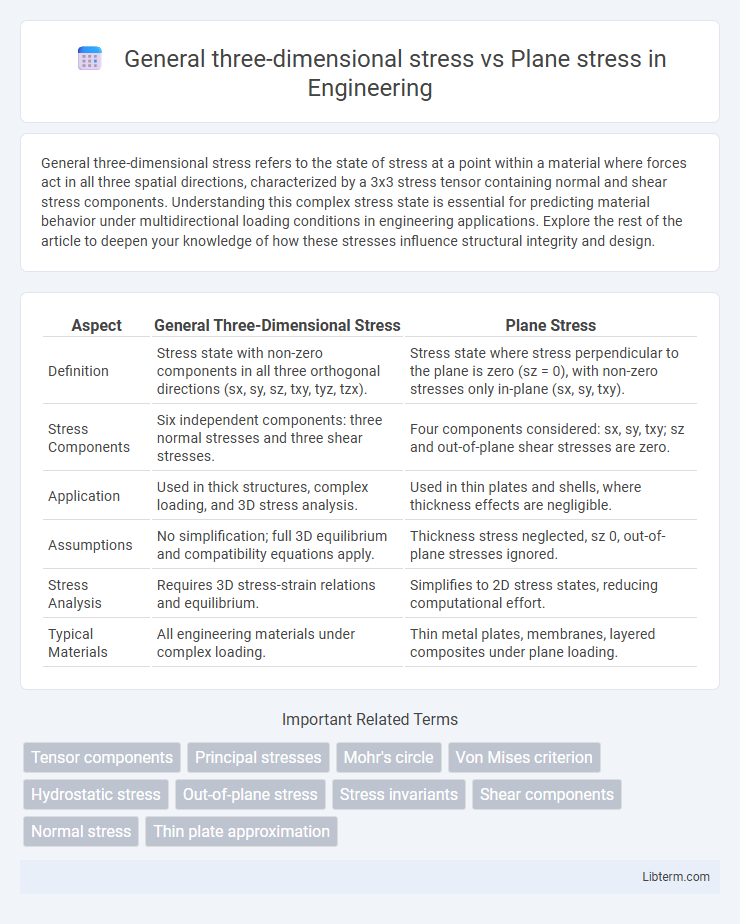
| Aspect | General Three-Dimensional Stress | Plane Stress |
|---|---|---|
| Definition | Stress state with non-zero components in all three orthogonal directions (sx, sy, sz, txy, tyz, tzx). | Stress state where stress perpendicular to the plane is zero (sz = 0), with non-zero stresses only in-plane (sx, sy, txy). |
| Stress Components | Six independent components: three normal stresses and three shear stresses. | Four components considered: sx, sy, txy; sz and out-of-plane shear stresses are zero. |
| Application | Used in thick structures, complex loading, and 3D stress analysis. | Used in thin plates and shells, where thickness effects are negligible. |
| Assumptions | No simplification; full 3D equilibrium and compatibility equations apply. | Thickness stress neglected, sz 0, out-of-plane stresses ignored. |
| Stress Analysis | Requires 3D stress-strain relations and equilibrium. | Simplifies to 2D stress states, reducing computational effort. |
| Typical Materials | All engineering materials under complex loading. | Thin metal plates, membranes, layered composites under plane loading. |
Introduction to Three-Dimensional Stress
Three-dimensional stress analysis considers stresses acting on all three mutually perpendicular planes, capturing the complete stress state within a solid body. Unlike plane stress, which assumes negligible stress components perpendicular to the plane, three-dimensional stress includes normal and shear stresses along the x, y, and z axes, essential for accurately predicting material behavior under complex loading conditions. This comprehensive approach is critical in fields like structural engineering and materials science, where precise stress evaluation ensures safety and performance.
Fundamentals of Plane Stress Condition
Plane stress condition assumes that stresses perpendicular to the plane (s_z, t_xz, t_yz) are negligible, simplifying three-dimensional stress analysis to two dimensions. This approximation is valid in thin structures where thickness is small compared to other dimensions, such as plates or shells. The fundamental concept reduces complexity, enabling effective evaluation of in-plane stresses s_x, s_y, and shear stress t_xy without considering out-of-plane stresses.
Mathematical Representation of 3D Stress
The mathematical representation of three-dimensional stress is expressed by a 3x3 symmetric stress tensor indicating normal and shear stresses acting on three mutually perpendicular planes, typically denoted as s_xx, s_yy, s_zz for normal stresses and t_xy, t_xz, t_yz for shear stresses. In contrast, plane stress simplifies this tensor by assuming negligible stress components perpendicular to the plane, reducing the stress state to a 2x2 matrix primarily involving s_xx, s_yy, and t_xy. The full 3D stress tensor enables comprehensive analysis of material behavior under complex loading, essential for accurate modeling in solid mechanics and finite element analysis.
Assumptions in Plane Stress Analysis
Plane stress analysis assumes that stresses perpendicular to the plane, specifically the out-of-plane normal stress and shear stresses, are negligible, simplifying the three-dimensional stress state into two dimensions. This assumption holds true for thin structures where thickness is small compared to other dimensions, allowing the thickness direction stress components (s_z, t_xz, t_yz) to be approximated as zero. By neglecting these stress components, plane stress models reduce computational complexity while providing accurate stress predictions for thin plates and shells subjected to in-plane loading.
Key Differences Between 3D Stress and Plane Stress
General three-dimensional stress involves stress components acting in all three spatial directions (x, y, and z) including normal and shear stresses, resulting in a 6-component stress tensor. Plane stress is a simplified condition where stress components perpendicular to the plane (typically the thickness direction) are assumed to be zero, reducing the stress state to a 3-component tensor within a two-dimensional plane. The key difference lies in dimensionality and complexity: 3D stress accounts for full volumetric stress interactions, while plane stress applies primarily to thin structures where out-of-plane stresses are negligible.
Physical Applications of Three-Dimensional Stress
General three-dimensional stress analysis captures the complete state of stress at a point, essential for accurately predicting failure in complex structures such as pressure vessels, aircraft fuselage, and biomedical implants where multi-axial loads occur. Unlike plane stress, which assumes negligible stress in one direction and is limited to thin flat components, three-dimensional stress considers normal and shear stresses on all faces of an element, enabling realistic simulation of stress distributions in thick materials and components under dynamic or thermal loading. This comprehensive approach supports advanced applications in finite element analysis for automotive crash simulations, geotechnical engineering in earth pressure computations, and design of composite materials subjected to multidirectional forces.
Typical Scenarios for Plane Stress
Typical scenarios for plane stress occur in thin structures such as metal plates, aircraft wings, and thin shells where the thickness is small compared to other dimensions. Stress components perpendicular to the plane, typically the thickness direction, are negligible, simplifying analysis to two-dimensional stress states. This assumption enables engineers to model and analyze stresses effectively in applications involving thin films, membranes, and structural components subjected to in-plane loads.
Stress Tensor in 3D vs 2D
The general three-dimensional stress state is represented by a 3x3 stress tensor containing nine components, including normal and shear stresses acting on all three spatial planes (x, y, z), which captures the complete stress distribution within a volume. In contrast, plane stress assumes negligible out-of-plane stresses, reducing the stress tensor to a 2x2 matrix with only four components, simplifying analysis to two dimensions typically within the xy-plane. This reduction significantly affects the mathematical modeling of stress and strain, enabling more efficient solutions in thin structures where thickness stresses are insignificant.
Implications for Structural Design
General three-dimensional stress considers the full state of stress at a point, capturing normal and shear stresses on all three axes, which is critical for accurately predicting failure in thick or complex structures. Plane stress assumes stress is negligible in the thickness direction, simplifying analysis for thin plates and shells while potentially underestimating stress concentrations in thicker components. Structural design must select the appropriate stress model to ensure safety and material efficiency, with three-dimensional stress models providing more precise failure predictions for load-bearing elements subject to complex loading.
Summary and Final Remarks
General three-dimensional stress encompasses all normal and shear stress components acting on a material element, capturing the complete state of stress in three mutually perpendicular directions. Plane stress simplifies this condition by assuming negligible stress in the thickness direction, often used in thin structures where out-of-plane stresses are minimal. The choice between general three-dimensional stress and plane stress models depends on the geometry and loading conditions, with plane stress providing computational efficiency for thin plates while three-dimensional stress analysis is essential for thick or complex components.
General three-dimensional stress Infographic
 libterm.com
libterm.com