A compliance matrix systematically organizes requirements and corresponding evidence of adherence, ensuring every specification is addressed accurately. This tool helps streamline audits, project reviews, and regulatory assessments by clearly mapping obligations to deliverables. Explore the rest of the article to learn how a compliance matrix can enhance Your project management and regulatory compliance strategies.
Table of Comparison
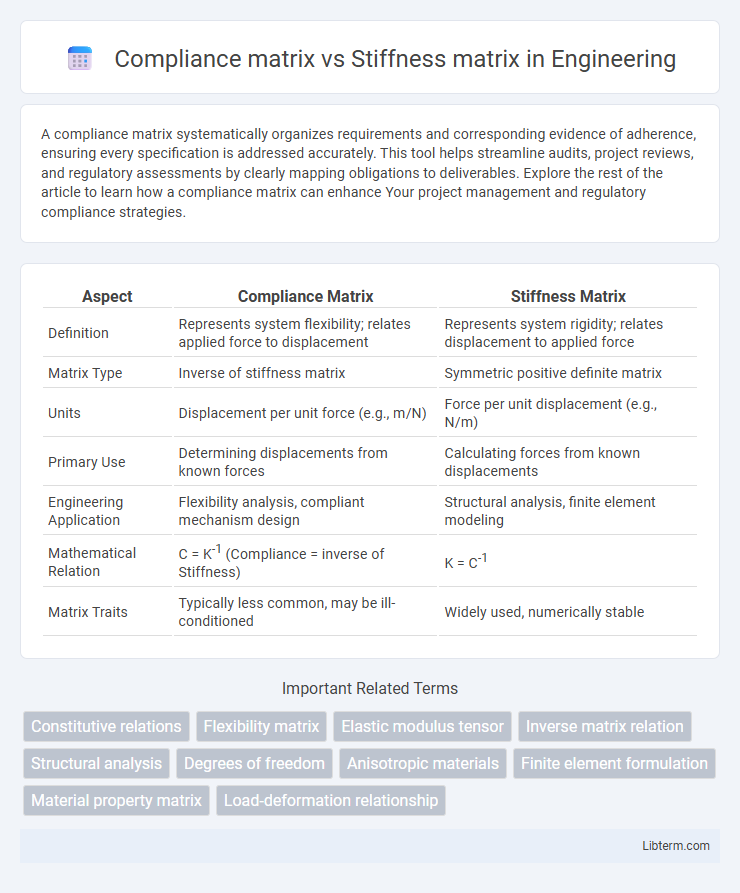
| Aspect | Compliance Matrix | Stiffness Matrix |
|---|---|---|
| Definition | Represents system flexibility; relates applied force to displacement | Represents system rigidity; relates displacement to applied force |
| Matrix Type | Inverse of stiffness matrix | Symmetric positive definite matrix |
| Units | Displacement per unit force (e.g., m/N) | Force per unit displacement (e.g., N/m) |
| Primary Use | Determining displacements from known forces | Calculating forces from known displacements |
| Engineering Application | Flexibility analysis, compliant mechanism design | Structural analysis, finite element modeling |
| Mathematical Relation | C = K-1 (Compliance = inverse of Stiffness) | K = C-1 |
| Matrix Traits | Typically less common, may be ill-conditioned | Widely used, numerically stable |
Introduction to Compliance and Stiffness Matrices
Compliance and stiffness matrices are fundamental concepts in structural mechanics used to describe material deformation under load. The compliance matrix relates applied forces to resulting displacements, representing flexibility and inverse rigidity, while the stiffness matrix connects displacements to corresponding forces, quantifying resistance to deformation. These matrices serve as essential tools in finite element analysis to model and predict structural behavior accurately.
Fundamental Definitions: Compliance vs. Stiffness
The compliance matrix defines the relationship between applied stress and resulting strain, representing a material's flexibility and deformation response under load. The stiffness matrix, conversely, correlates strain with applied stress, emphasizing resistance to deformation and structural rigidity. Fundamentally, the compliance matrix is the inverse of the stiffness matrix, illustrating complementary perspectives on material mechanical behavior.
Mathematical Representation and Notation
The compliance matrix, denoted as [S], represents the inverse of the stiffness matrix [K], relating strain to applied stress through strain = [S] x stress, while the stiffness matrix relates stress to strain via stress = [K] x strain. Mathematically, the stiffness matrix [K] is symmetric and positive definite, containing material stiffness coefficients, whereas the compliance matrix [S] contains flexibility coefficients and satisfies [S] = [K]-1. Notation conventionally uses [K] for stiffness in units of force per unit displacement and [S] for compliance in units of displacement per unit force, emphasizing their inverse relationship in linear elasticity.
Physical Interpretation in Engineering Systems
The compliance matrix represents the flexibility of an engineering system, quantifying the displacement response under applied forces, whereas the stiffness matrix characterizes the system's resistance to deformation by relating forces to displacements. In structural analysis, the compliance matrix is the inverse of the stiffness matrix, reflecting how physical systems deform under loads versus how they resist those loads. Understanding these matrices aids in modeling material behavior, optimizing design for strength, and predicting performance under mechanical stresses.
Key Differences Between Compliance and Stiffness Matrices
The compliance matrix relates applied stresses to resulting strains, representing material flexibility, whereas the stiffness matrix relates strains to stresses, indicating material rigidity. Compliance matrices are used in flexibility analyses to determine deformation under loads, while stiffness matrices are fundamental in structural analysis and finite element methods for calculating resistance. Compliance is the inverse of stiffness, making the key difference their representation of opposite mechanical properties in elasticity theory.
Applications in Structural Analysis
The compliance matrix and stiffness matrix are fundamental in structural analysis, characterizing material deformation and resistance under load. The stiffness matrix is widely used in finite element analysis (FEA) to determine displacements and internal forces by relating nodal displacements to applied loads. Conversely, the compliance matrix, being the inverse of the stiffness matrix, finds application in inverse problems and material property identification where strains are used to infer stresses.
Calculation Methods and Example Problems
Compliance matrix and stiffness matrix are fundamental in structural mechanics, each reflecting material behavior under load; the compliance matrix relates strain to applied stress using inverse calculation methods, while the stiffness matrix connects force to displacement through direct calculation methods. Calculation methods for compliance matrices typically involve inverting the stiffness matrix, which is derived from constitutive equations or finite element models, allowing engineers to solve for strain given known stresses. Example problems often include analyzing cantilever beams where the stiffness matrix predicts displacements under applied loads, and the compliance matrix is used to find strain responses under specified stresses, illustrating their complementary roles in mechanical analysis.
Conversion Between Compliance and Stiffness Matrices
The compliance matrix and stiffness matrix are inversely related, where the compliance matrix (S) represents flexibility and the stiffness matrix (K) denotes rigidity of a material or structure. Conversion between these matrices involves matrix inversion, with the stiffness matrix calculated as the inverse of the compliance matrix (K = S^-1) and vice versa (S = K^-1). Accurate transformation is essential for applications in structural analysis and material science to ensure precise stress-strain predictions and mechanical behavior modeling.
Advantages and Limitations of Each Approach
The compliance matrix offers direct insight into material flexibility by relating applied forces to resulting displacements, making it advantageous for analyzing systems where deformation is critical, but it can become computationally intensive for large, complex structures. The stiffness matrix, preferred in finite element analysis, efficiently captures resistance to deformation by linking nodal displacements to applied forces, facilitating stable numerical solutions; however, it may obscure intuitive understanding of material compliance. Both approaches require careful consideration of boundary conditions and system symmetry to maximize accuracy and computational efficiency in structural and mechanical simulations.
Conclusion: Choosing the Right Matrix for Analysis
Compliance matrix and stiffness matrix both serve crucial roles in structural analysis, with the stiffness matrix relating forces to displacements and the compliance matrix linking displacements to forces. Selecting the right matrix depends on the problem context--stiffness matrices are preferred for their direct formulation in finite element methods and structural design, while compliance matrices are valuable in inverse problems and systems emphasizing flexibility. Engineers must evaluate computational efficiency, problem requirements, and numerical stability to determine the optimal matrix for accurate and effective analysis.
Compliance matrix Infographic
 libterm.com
libterm.com