A quasistatic state refers to a process or condition in which a system changes so slowly that it remains nearly in equilibrium at all times, ensuring minimal deviation from a true steady state. This concept is crucial in thermodynamics and physics to analyze reversible processes and understand system behavior under infinitesimally small changes. Explore the rest of the article to deepen your understanding of quasistatic states and their applications.
Table of Comparison
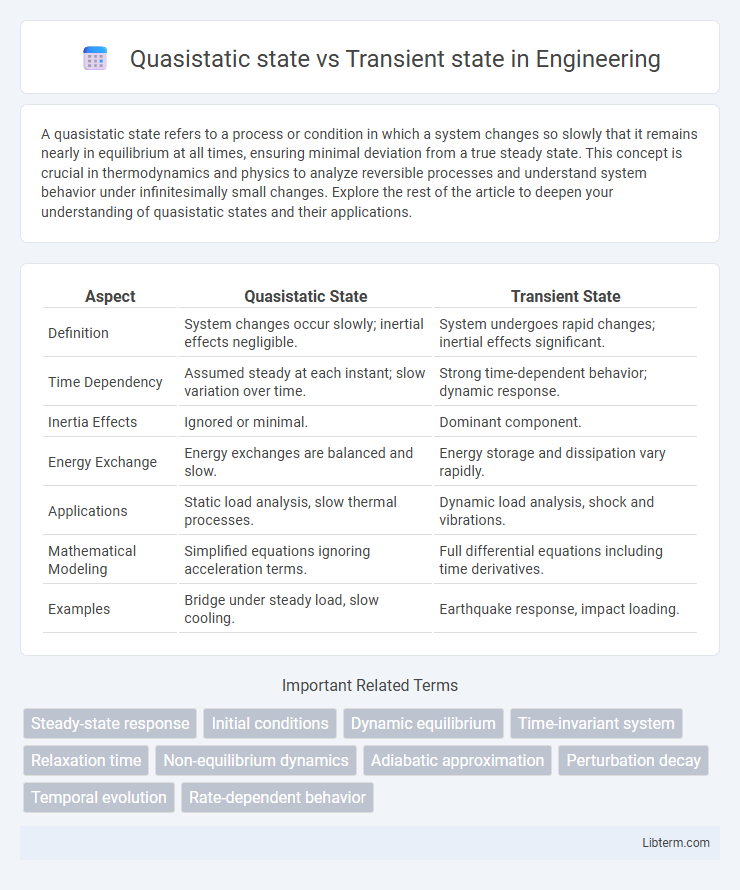
| Aspect | Quasistatic State | Transient State |
|---|---|---|
| Definition | System changes occur slowly; inertial effects negligible. | System undergoes rapid changes; inertial effects significant. |
| Time Dependency | Assumed steady at each instant; slow variation over time. | Strong time-dependent behavior; dynamic response. |
| Inertia Effects | Ignored or minimal. | Dominant component. |
| Energy Exchange | Energy exchanges are balanced and slow. | Energy storage and dissipation vary rapidly. |
| Applications | Static load analysis, slow thermal processes. | Dynamic load analysis, shock and vibrations. |
| Mathematical Modeling | Simplified equations ignoring acceleration terms. | Full differential equations including time derivatives. |
| Examples | Bridge under steady load, slow cooling. | Earthquake response, impact loading. |
Introduction to Quasistatic and Transient States
Quasistatic states refer to processes that occur slowly enough for the system to maintain equilibrium at all times, allowing variables to adjust gradually without inducing significant non-equilibrium effects. Transient states describe conditions where system variables change rapidly, causing non-equilibrium behavior before reaching a new steady state or equilibrium. Understanding the distinction between quasistatic and transient states is crucial for analyzing dynamic system responses in thermodynamics, fluid mechanics, and control systems.
Defining Quasistatic State
A quasistatic state refers to a process occurring sufficiently slowly such that the system remains in near-equilibrium throughout, allowing thermodynamic variables to be well-defined at every instant. Unlike transient states, where rapid changes drive the system out of equilibrium, quasistatic processes assume infinitesimal deviations from equilibrium conditions, enabling precise analysis using equilibrium thermodynamics. This concept is critical in thermodynamics and mechanical systems, ensuring predictable and reversible behavior during energy transformations.
Defining Transient State
The transient state refers to the temporary period during which a system undergoes changes before reaching a new equilibrium or steady state. It is characterized by time-dependent variations in system variables such as temperature, pressure, or voltage, unlike the quasistatic state where changes occur infinitely slowly, maintaining equilibrium at every moment. Understanding transient states is crucial in fields like thermodynamics, electrical engineering, and fluid dynamics to analyze system response and stability during dynamic processes.
Key Differences between Quasistatic and Transient States
Quasistatic states describe processes occurring slowly enough for the system to remain in near-equilibrium at all times, with negligible changes in state variables over time. Transient states involve rapid changes where the system moves between equilibrium points, causing significant temporal variations in properties like pressure, temperature, and velocity. The key difference lies in the time scale and rate of change; quasistatic processes approximate steady-state conditions, while transient processes capture dynamic, time-dependent behaviors.
Physical Examples of Quasistatic States
A quasistatic state occurs when a system changes so slowly that it passes through a series of equilibrium states, such as the slow compression of a gas in a piston or the gradual heating of a metal rod allowing uniform temperature distribution. These processes contrast with transient states where rapid changes prevent equilibrium, exemplified by sudden voltage changes in electrical circuits or immediate temperature shifts in chemical reactions. Physical examples of quasistatic states include the isothermal compression of an ideal gas, slow deformation in viscoelastic materials, and steady heat conduction through a solid slab.
Real-World Applications of Transient States
Transient states are crucial in designing automotive braking systems where rapid changes in motion require analysis of non-steady conditions to ensure safety and performance. Power grid management relies on transient state analysis to handle sudden fluctuations in load or faults, preventing blackouts and equipment damage. In electronics, transient responses determine the stability and speed of circuits during switching operations, directly impacting device reliability and efficiency.
Mathematical Representation of Quasistatic Processes
Quasistatic processes are mathematically represented by a series of equilibrium states where variables change infinitesimally slowly, allowing differential equations to describe the system's behavior with time derivatives approaching zero. In contrast, transient states involve rapid changes described by time-dependent partial differential equations capturing dynamic, non-equilibrium phenomena. The quasistatic assumption simplifies analysis by enabling the use of static equations at each instant, making it crucial in thermodynamics and continuum mechanics for modeling near-equilibrium conditions.
Mathematical Modeling of Transient Behavior
In the mathematical modeling of transient behavior, transient state describes the period when system variables change with time before reaching equilibrium, often represented by differential equations incorporating initial conditions and time-dependent parameters. Quasistatic state assumes instantaneous equilibrium, allowing simplification to algebraic equations by neglecting time derivatives, suitable only when transient effects are negligible. Accurate transient analysis requires solving partial or ordinary differential equations, such as the heat equation or mass transfer equations, to predict temporal evolution in physical systems.
Importance in Engineering and Physics
Understanding the quasistatic state is crucial in engineering and physics for analyzing systems that change so slowly the system is almost in equilibrium at every moment, simplifying complex calculations in thermodynamics and mechanics. Transient state analysis is essential for designing and controlling systems experiencing rapid changes, such as electrical circuits, heat transfer, and fluid flow, ensuring stability and performance during non-equilibrium conditions. Both states provide fundamental insights for optimizing system design, enhancing safety, and predicting real-world behavior under various operating conditions.
Summary: Choosing Between Quasistatic and Transient Analysis
Quasistatic analysis assumes that loads are applied slowly enough for inertial effects to be negligible, making it ideal for studying equilibrium states in mechanical and structural systems. Transient analysis accounts for time-dependent changes and dynamic effects, necessary for accurately capturing system responses during rapid load variations or shocks. Selecting between these methods depends on the rate of load application, the significance of dynamic forces, and the precision required for temporal response predictions.
Quasistatic state Infographic
 libterm.com
libterm.com