The Euler number is a fundamental constant in mathematics, approximately equal to 2.71828, and serves as the base of natural logarithms. It plays a crucial role in calculus, complex analysis, and many areas of science such as growth processes and compound interest calculations. Discover how the Euler number impacts various fields and why understanding your use of it can enhance problem-solving by reading the rest of the article.
Table of Comparison
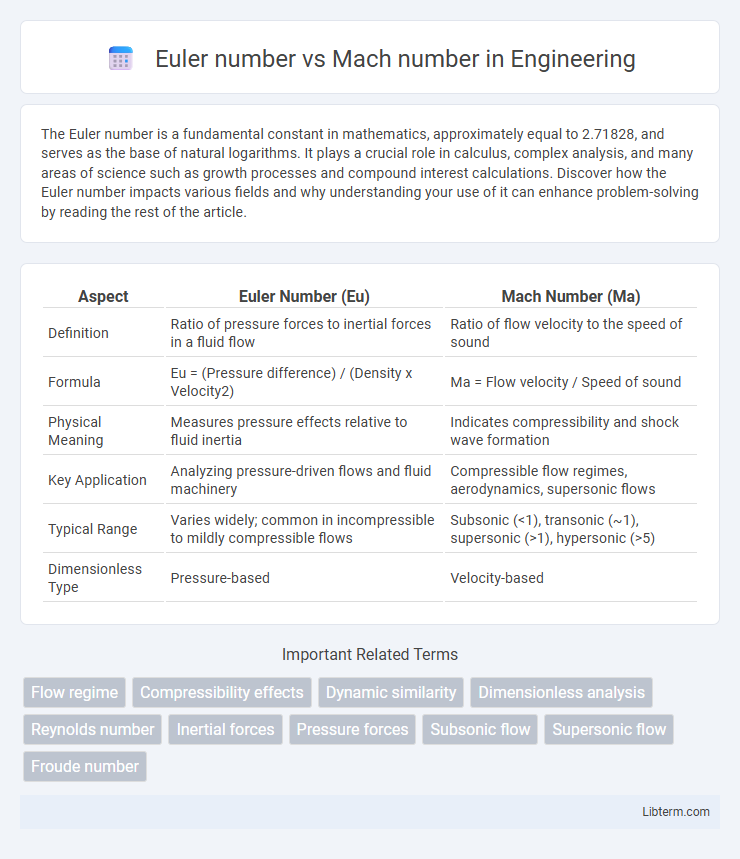
| Aspect | Euler Number (Eu) | Mach Number (Ma) |
|---|---|---|
| Definition | Ratio of pressure forces to inertial forces in a fluid flow | Ratio of flow velocity to the speed of sound |
| Formula | Eu = (Pressure difference) / (Density x Velocity2) | Ma = Flow velocity / Speed of sound |
| Physical Meaning | Measures pressure effects relative to fluid inertia | Indicates compressibility and shock wave formation |
| Key Application | Analyzing pressure-driven flows and fluid machinery | Compressible flow regimes, aerodynamics, supersonic flows |
| Typical Range | Varies widely; common in incompressible to mildly compressible flows | Subsonic (<1), transonic (~1), supersonic (>1), hypersonic (>5) |
| Dimensionless Type | Pressure-based | Velocity-based |
Introduction to Euler Number and Mach Number
Euler number (Eu) quantifies the ratio of pressure forces to inertial forces in fluid flow, expressing the significance of pressure differences in a system. Mach number (Ma) represents the ratio of an object's speed to the speed of sound, indicating compressibility effects in high-speed fluid dynamics. Both dimensionless numbers are critical in aerodynamics and fluid mechanics for analyzing flow regimes and characterizing shock waves or pressure variations.
Fundamental Definitions
The Euler number (Eu) is a dimensionless parameter representing the ratio of pressure forces to inertial forces within a fluid flow, defined as Eu = DP / (r u2), where DP is the pressure difference, r is fluid density, and u is flow velocity. The Mach number (Ma) quantifies the ratio of flow velocity to the local speed of sound, Ma = u / c, indicating compressibility effects in high-speed aerodynamics. While the Euler number emphasizes pressure-driven flow characteristics, the Mach number primarily addresses compressibility and wave propagation phenomena in gases.
Physical Significance of Euler Number
The Euler number (Eu) represents the ratio of pressure forces to inertial forces within a fluid flow, highlighting the impact of pressure differences on fluid motion. It is crucial in analyzing flow regimes where pressure variations dominate, such as in pumps, turbines, and hydraulic systems. Unlike the Mach number, which relates flow velocity to the speed of sound and compressibility effects, the Euler number emphasizes pressure-driven phenomena in incompressible or mildly compressible fluids.
Physical Significance of Mach Number
The Mach number represents the ratio of an object's speed to the speed of sound in the surrounding medium, providing critical insight into compressibility effects and flow regime classification in fluid dynamics. It determines the transition between subsonic, transonic, supersonic, and hypersonic flows, influencing shock wave formation and aerodynamic heating. Unlike the Euler number, which relates pressure forces to inertial forces, the Mach number directly quantifies the impact of velocity relative to acoustic propagation speed on flow behavior.
Mathematical Expressions and Units
Euler number (Eu) is a dimensionless parameter defined as the ratio of pressure forces to inertial forces, expressed mathematically as Eu = DP / (ru2), where DP represents the pressure difference (Pa), r is the fluid density (kg/m3), and u is the characteristic velocity (m/s). Mach number (Ma) quantifies the ratio of flow velocity to the local speed of sound, given by Ma = u / a, with u as flow velocity (m/s) and a as speed of sound in the medium (m/s). While both are dimensionless, Euler number relates pressure variations to flow dynamics, and Mach number characterizes compressibility effects in fluid flow.
Key Differences Between Euler and Mach Numbers
Euler number quantifies the ratio of pressure forces to inertial forces in fluid flow and is essential in characterizing flow behavior in compressible and incompressible regimes. Mach number measures the flow velocity relative to the speed of sound, indicating subsonic, transonic, or supersonic conditions critical for aerodynamic and shock wave analysis. While Euler number emphasizes pressure-inertia balance, Mach number focuses on velocity effects and compressibility in high-speed fluid dynamics.
Applications in Fluid Dynamics
Euler number and Mach number serve distinct roles in fluid dynamics applications by characterizing different flow properties. The Euler number quantifies the ratio of pressure forces to inertial forces, aiding in the analysis of compressible and incompressible fluid flow, especially in predicting pressure drops and cavitation in pumps and turbines. The Mach number determines flow regime classification based on flow velocity relative to the speed of sound, critical in aerospace engineering for designing supersonic jets and understanding shock wave formation.
Impact on Flow Regimes
Euler number (Eu) and Mach number (Ma) both critically influence flow regimes, with Euler number representing the ratio of pressure forces to inertial forces and Mach number indicating the ratio of flow velocity to the speed of sound. High Euler numbers typically correlate with flows dominated by pressure variations, impacting incompressible or low-speed regimes, while Mach number dictates compressibility effects and shock wave formation in high-speed flows. Understanding the interplay between Eu and Ma facilitates accurate prediction of flow behavior, such as transition from subsonic to supersonic regimes and the resulting impact on aerodynamic stability and heat transfer.
Practical Examples and Case Studies
Euler number and Mach number are critical dimensionless parameters in fluid dynamics, each serving distinct practical applications. Euler number, defined as the ratio of pressure forces to inertial forces, is extensively used in pump and valve performance analysis to evaluate pressure drops and flow resistance in pipelines, as demonstrated in hydraulic system case studies. Mach number, representing the ratio of flow velocity to the speed of sound, is crucial in aerospace engineering, with numerous case studies analyzing supersonic aircraft behavior, shock wave formation, and aerodynamic heating at high velocities.
Conclusion: Choosing the Right Dimensionless Number
Selecting the appropriate dimensionless number depends on the specific fluid dynamics problem: use the Euler number to analyze pressure forces relative to inertial forces in compressible flow scenarios, while the Mach number is essential for characterizing flow speed relative to the speed of sound and identifying compressibility effects. For high-speed aerodynamics and shock wave studies, the Mach number provides critical insight, whereas the Euler number is more relevant in pressure-driven flow analyses and incompressible flow regimes. Proper application of these dimensionless numbers ensures accurate modeling and prediction of fluid behavior under varying flow conditions.
Euler number Infographic
 libterm.com
libterm.com