Integral control eliminates steady-state error by continuously summing the past error over time, making real-time adjustments to the system output. This control strategy plays a critical role in maintaining desired system performance in various applications, from industrial automation to temperature regulation. Explore the rest of this article to understand how integral control can enhance your system's stability and accuracy.
Table of Comparison
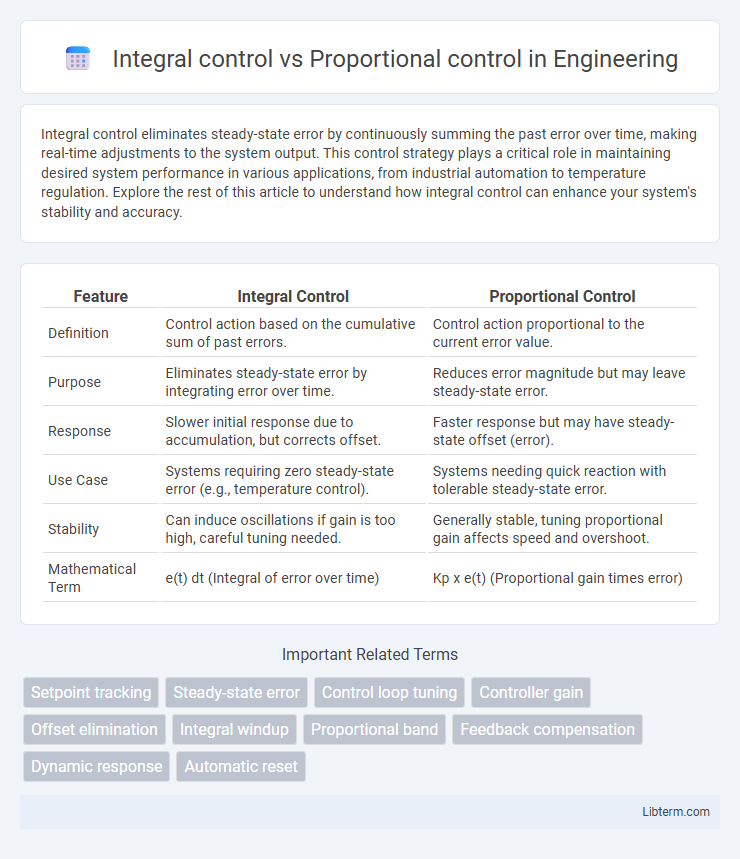
| Feature | Integral Control | Proportional Control |
|---|---|---|
| Definition | Control action based on the cumulative sum of past errors. | Control action proportional to the current error value. |
| Purpose | Eliminates steady-state error by integrating error over time. | Reduces error magnitude but may leave steady-state error. |
| Response | Slower initial response due to accumulation, but corrects offset. | Faster response but may have steady-state offset (error). |
| Use Case | Systems requiring zero steady-state error (e.g., temperature control). | Systems needing quick reaction with tolerable steady-state error. |
| Stability | Can induce oscillations if gain is too high, careful tuning needed. | Generally stable, tuning proportional gain affects speed and overshoot. |
| Mathematical Term | e(t) dt (Integral of error over time) | Kp x e(t) (Proportional gain times error) |
Introduction to Control Systems
Integral control eliminates steady-state error by integrating the error signal over time, enhancing system accuracy compared to proportional control, which adjusts output based solely on current error magnitude. Proportional control provides faster response but may result in persistent offset, whereas integral control ensures zero steady-state error by accumulating past errors to correct the system output. In control systems design, combining proportional and integral actions in a PI controller optimizes stability and performance by addressing both transient and steady-state behaviors.
Understanding Proportional Control
Proportional control regulates a system's output by adjusting the control signal proportionally to the error, the difference between the desired setpoint and the measured process variable. This method provides a straightforward and immediate response, effectively reducing steady-state error and maintaining system stability in many industrial applications. While proportional control alone can prevent large deviations, it often requires integration with integral control to eliminate residual offset and achieve precise long-term accuracy.
Fundamentals of Integral Control
Integral control eliminates steady-state error by continuously summing the error over time, ensuring the output reaches and maintains the desired setpoint. Unlike proportional control, which reacts only to the current error magnitude, integral control adjusts based on the cumulative error, improving accuracy in systems with persistent disturbances. This fundamental approach enhances system stability and precision in process control applications.
Key Differences Between Proportional and Integral Control
Proportional control adjusts the control output proportionally to the current error, providing immediate response but often resulting in steady-state error. Integral control focuses on the accumulation of past errors, eliminating steady-state error by continuously adjusting the output until the error is zero. The key difference lies in proportional control addressing present error magnitude while integral control accounts for the history of error to improve accuracy over time.
Response to Setpoint Changes
Integral control eliminates steady-state error by continuously integrating the difference between the setpoint and the process variable, ensuring that the output eventually reaches and maintains the desired value despite persistent disturbances. Proportional control responds to setpoint changes by producing an output proportional to the current error, which provides a faster initial response but often results in a residual steady-state error. Combining integral and proportional control in a PI controller improves response time and accuracy, reducing offset while stabilizing the system output at the setpoint.
Handling Steady-State Errors
Integral control effectively eliminates steady-state errors by accumulating past error values and adjusting the control signal until the error reaches zero, ensuring precise long-term accuracy. Proportional control reacts proportionally to the current error but often leaves a residual steady-state error because it lacks a mechanism to address accumulated offsets. Combining integral action with proportional control (PI control) enhances system stability and accuracy by reducing steady-state error while maintaining responsive performance.
Stability and Oscillation Concerns
Integral control enhances system stability by eliminating steady-state errors but can introduce oscillations due to its accumulation effect, potentially causing overshoot if not properly tuned. Proportional control provides faster response and reduces oscillations by adjusting output in direct proportion to error magnitude but often results in a steady-state error. Balancing the integral and proportional gains in a PI controller is crucial to minimizing oscillations while maintaining stability and accurate steady-state performance.
Real-World Applications of Proportional Control
Proportional control is widely used in real-world applications such as temperature regulation in HVAC systems, speed control in electric motors, and fluid level management in industrial tanks due to its simplicity and quick response to error. Unlike integral control, which eliminates steady-state error by accumulating past errors, proportional control delivers immediate adjustments proportional to the current error, making it ideal for processes requiring rapid stabilization. This control strategy is essential in scenarios where system dynamics are well-understood and fast correction without overshoot is necessary.
Practical Uses of Integral Control
Integral control is widely used in practical applications requiring elimination of steady-state errors, such as temperature regulation in HVAC systems and speed control in motors. Its ability to accumulate past errors allows precise long-term adjustments, making it essential in processes with constant disturbances or changes in load. Unlike proportional control, integral control ensures accurate setpoint tracking by continuously correcting deviations over time.
Choosing the Right Control Method
Integral control eliminates steady-state error by continuously summing past errors, making it ideal for systems requiring precise long-term accuracy. Proportional control responds to current error magnitude with faster reaction times but may result in persistent offset. Selecting the right control method depends on system dynamics, desired response speed, and tolerance for steady-state error, often combining both in a Proportional-Integral (PI) controller for balanced performance.
Integral control Infographic
 libterm.com
libterm.com