Compressible flow involves fluid dynamics where changes in density significantly affect the flow behavior, often observed in gases at high velocities or varying pressures. Understanding shock waves, expansions, and Mach number effects is crucial for applications in aerospace, engineering, and gas dynamics. Explore the rest of the article to deepen your knowledge of compressible flow phenomena and their practical implications.
Table of Comparison
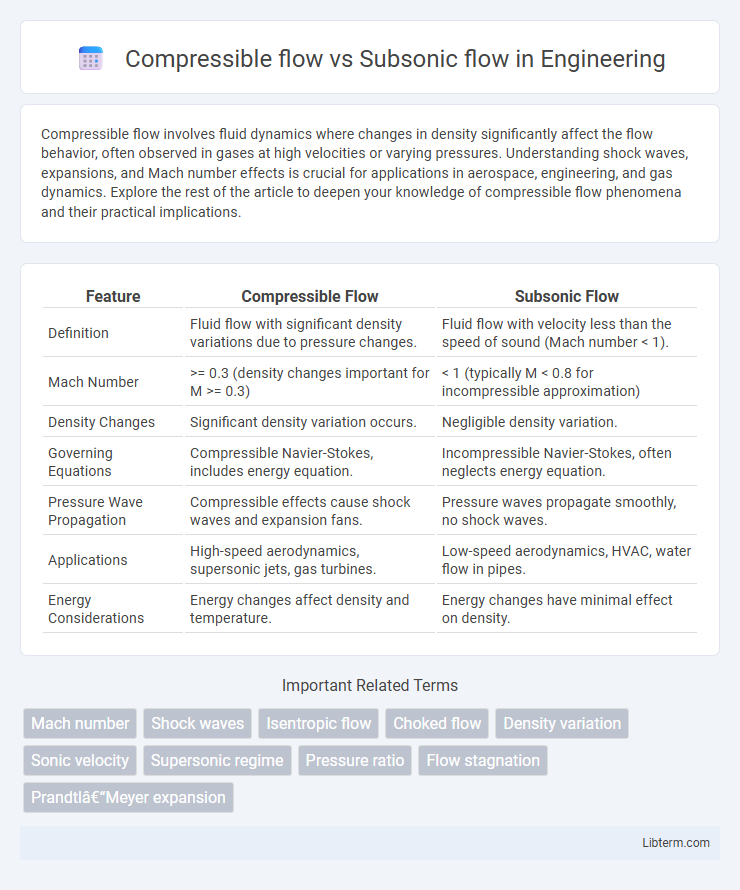
| Feature | Compressible Flow | Subsonic Flow |
|---|---|---|
| Definition | Fluid flow with significant density variations due to pressure changes. | Fluid flow with velocity less than the speed of sound (Mach number < 1). |
| Mach Number | >= 0.3 (density changes important for M >= 0.3) | < 1 (typically M < 0.8 for incompressible approximation) |
| Density Changes | Significant density variation occurs. | Negligible density variation. |
| Governing Equations | Compressible Navier-Stokes, includes energy equation. | Incompressible Navier-Stokes, often neglects energy equation. |
| Pressure Wave Propagation | Compressible effects cause shock waves and expansion fans. | Pressure waves propagate smoothly, no shock waves. |
| Applications | High-speed aerodynamics, supersonic jets, gas turbines. | Low-speed aerodynamics, HVAC, water flow in pipes. |
| Energy Considerations | Energy changes affect density and temperature. | Energy changes have minimal effect on density. |
Introduction to Flow Regimes
Compressible flow occurs when fluid density changes significantly due to variations in pressure and temperature, typically at Mach numbers greater than 0.3, causing density to affect the flow characteristics. Subsonic flow refers to fluid motion at speeds below the speed of sound (Mach < 1), where density changes are negligible and incompressible flow assumptions often apply. Distinguishing these flow regimes is critical in aerodynamics and gas dynamics, as compressibility effects influence shock wave formation, pressure distribution, and aerodynamic forces.
Defining Compressible Flow
Compressible flow occurs when fluid density varies significantly within the flow field, typically at Mach numbers greater than 0.3, causing changes in pressure, temperature, and density to affect the fluid dynamics. Subsonic flow represents fluid motion at Mach numbers less than 1, where compressibility effects are often negligible, and density changes can be approximated as constant. Defining compressible flow involves recognizing scenarios where density variations influence continuity, momentum, and energy equations, differentiating it from incompressible or subsonic flow regimes.
Understanding Subsonic Flow
Subsonic flow is characterized by fluid velocities below the speed of sound, typically with a Mach number less than 0.8, allowing the assumption of incompressible flow in many practical applications. Compressible flow effects become negligible in subsonic regimes, enabling simplified analysis using constant density assumptions and Bernoulli's equation. Understanding subsonic flow is crucial for designing efficient aerodynamic shapes and predicting pressure and velocity distributions in airfoils, ducts, and ventilation systems.
Key Differences Between Compressible and Subsonic Flow
Compressible flow involves significant changes in fluid density, typically occurring at Mach numbers greater than 0.3, whereas subsonic flow is characterized by Mach numbers less than 1 and generally assumes constant density. Compressible flow analysis requires solving compressible Navier-Stokes equations due to variable density and pressure, while subsonic flow often uses incompressible flow approximations simplifying the mathematical treatment. Key differences include shock wave formation and temperature variations in compressible flow, which are absent in subsonic flow regimes.
Governing Equations for Each Flow Type
Compressible flow is governed by the full Navier-Stokes equations incorporating continuity, momentum, and energy equations with variable density and pressure-dependent thermodynamic properties, often described through the compressible form of the Euler equations for inviscid flow. Subsonic flow, a subset of compressible flow where Mach number is less than one, can often be simplified using incompressible flow assumptions, reducing the governing equations to the incompressible Navier-Stokes equations with constant density. The key distinction lies in handling density variations; compressible flow equations require coupling density, pressure, and temperature, while subsonic flow equations usually treat density as constant for low Mach numbers.
Mach Number and Its Significance
Mach number is a key parameter distinguishing compressible flow from subsonic flow, with compressible flow generally occurring at Mach numbers greater than 0.3, where variations in air density become significant. Subsonic flow, characterized by Mach numbers below 0.3, assumes incompressibility, allowing density changes to be neglected in flow analysis. The significance of Mach number lies in its role in determining aerodynamic behavior, flow properties, and the applicability of compressibility effects in fluid dynamics calculations.
Effects of Density Changes in Flow
Compressible flow involves significant variations in fluid density caused by pressure changes, which strongly influence velocity, temperature, and pressure distributions within the flow field. In contrast, subsonic flow typically assumes constant density, allowing simplifications in continuity and momentum equations, as density changes are negligible for Mach numbers below approximately 0.3. The effects of density changes in compressible flow are critical for accurate analysis of high-speed aerodynamics, shock wave formation, and energy transfer in gases, whereas subsonic flow models focus primarily on velocity and pressure without major density variation considerations.
Applications of Compressible Flow
Compressible flow is crucial in high-speed aerodynamics, particularly in the design of supersonic aircraft, rockets, and jet engines where density variations significantly affect performance. It also plays a vital role in gas dynamics applications such as nozzle flow, shock wave formation, and high-speed ventilation systems. Understanding compressible flow enables optimization of propulsion efficiency and thermal management in aerospace and mechanical engineering.
Common Uses of Subsonic Flow
Subsonic flow, characterized by flow velocities less than the speed of sound, is commonly used in applications such as commercial aviation, HVAC systems, and automotive aerodynamics due to its predictable pressure and temperature variations. Unlike compressible flow, which involves significant density changes and shock waves typically seen in supersonic and hypersonic regimes, subsonic flow generally assumes incompressible fluid behavior for simplified analysis and engineering design. This results in efficient performance in aircraft cruising at speeds below Mach 0.8 and the optimization of ventilation and ducting systems where pressure losses and noise reduction are critical.
Summary and Comparative Analysis
Compressible flow involves significant variations in fluid density, typically occurring at Mach numbers greater than 0.3, whereas subsonic flow assumes nearly constant density with Mach numbers less than 1. Compressible flow requires solving the full Navier-Stokes equations with variable density effects, capturing shock waves, expansion fans, and compressibility-related phenomena. Subsonic flow analysis simplifies to incompressible flow equations, neglecting density changes and shock waves, which results in different aerodynamic characteristics and engineering applications.
Compressible flow Infographic
 libterm.com
libterm.com