Clustering is a powerful technique in data analysis that groups similar data points to reveal hidden patterns and structures within large datasets. By segmenting data into meaningful clusters, it enables more efficient decision-making and personalized solutions tailored to your specific needs. Explore the rest of this article to discover how clustering can transform your data insights and drive smarter strategies.
Table of Comparison
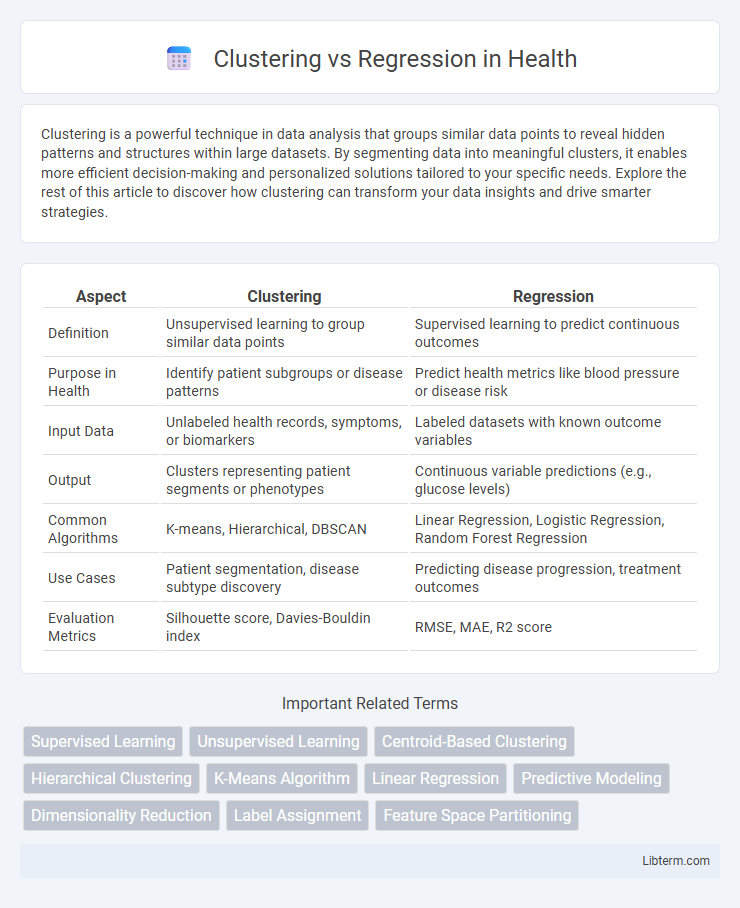
| Aspect | Clustering | Regression |
|---|---|---|
| Definition | Unsupervised learning to group similar data points | Supervised learning to predict continuous outcomes |
| Purpose in Health | Identify patient subgroups or disease patterns | Predict health metrics like blood pressure or disease risk |
| Input Data | Unlabeled health records, symptoms, or biomarkers | Labeled datasets with known outcome variables |
| Output | Clusters representing patient segments or phenotypes | Continuous variable predictions (e.g., glucose levels) |
| Common Algorithms | K-means, Hierarchical, DBSCAN | Linear Regression, Logistic Regression, Random Forest Regression |
| Use Cases | Patient segmentation, disease subtype discovery | Predicting disease progression, treatment outcomes |
| Evaluation Metrics | Silhouette score, Davies-Bouldin index | RMSE, MAE, R2 score |
Introduction to Clustering and Regression
Clustering and regression are fundamental techniques in data analysis with distinct purposes and applications. Clustering groups data points based on similarity, facilitating pattern recognition and segmentation without predefined labels, often used in customer segmentation and image analysis. Regression predicts continuous outcomes by modeling relationships between dependent and independent variables, widely applied in forecasting sales, risk assessment, and trend analysis.
Definition of Clustering
Clustering is an unsupervised machine learning technique that groups data points based on similarity or distance metrics without predefined labels. It identifies inherent structures or patterns by partitioning data into clusters where members share common features. Unlike regression, which predicts continuous outcomes, clustering focuses on discovering natural groupings within the dataset.
Definition of Regression
Regression is a supervised learning technique used to predict continuous numerical values based on relationships between dependent and independent variables. It models the correlation by fitting a function, typically a line or curve, that minimizes the error between observed and predicted outcomes. Unlike clustering, which groups data without predefined labels, regression requires labeled training data to forecast future or unseen numerical results accurately.
Key Differences Between Clustering and Regression
Clustering involves grouping data points into clusters based on similarity without predefined labels, serving as an unsupervised learning technique primarily for data segmentation. Regression predicts continuous numerical outcomes using labeled input-output pairs, functioning as a supervised learning method aimed at forecasting or trend estimation. The key difference lies in clustering's goal to discover inherent data structures, whereas regression focuses on modeling relationships to predict specific values.
Techniques Used in Clustering
Clustering techniques in data analysis primarily include K-means, hierarchical clustering, and DBSCAN, which group data points based on similarity without predefined labels. These methods optimize intra-cluster similarity and inter-cluster dissimilarity using distance metrics like Euclidean or Manhattan distance. Unlike regression, clustering is an unsupervised learning technique that identifies inherent structures within datasets rather than predicting continuous outcomes.
Techniques Used in Regression
Regression techniques primarily include linear regression, polynomial regression, ridge regression, and lasso regression, each designed to model the relationship between dependent and independent variables by minimizing the error in predictions. Advanced methods like support vector regression (SVR) and decision tree regression further enhance flexibility to capture non-linear patterns and interactions. These techniques employ optimization algorithms such as gradient descent to fit models that predict continuous outcomes, differing from clustering methods that group data without predefined labels.
Typical Applications of Clustering
Clustering is commonly used in customer segmentation to identify distinct groups based on purchasing behavior or demographics, enabling targeted marketing strategies. It plays a crucial role in image segmentation for medical imaging, facilitating the identification of tumors or abnormalities by grouping pixels with similar features. Clustering also aids anomaly detection in network security by grouping normal activity patterns and isolating outliers indicating potential cyber threats.
Typical Applications of Regression
Regression is widely used in predicting continuous outcomes such as sales forecasting, housing price estimation, and risk assessment in finance. It models relationships between dependent and independent variables to quantify trends and make data-driven predictions. Typical applications include demand forecasting, medical outcome prediction, and customer lifetime value estimation.
Challenges in Clustering and Regression
Clustering faces challenges such as determining the optimal number of clusters, handling high-dimensional data, and dealing with noisy or overlapping data points that can obscure clear group boundaries. Regression struggles with assumptions about the data distribution, multicollinearity among predictor variables, and the potential for overfitting, especially in models with numerous predictors relative to sample size. Both methods require careful preprocessing and model selection to ensure accurate and meaningful results in practical applications.
Choosing the Right Approach: Clustering or Regression
Choosing the right approach between clustering and regression depends primarily on your data's nature and the analysis goal. Use clustering when you need to identify natural groupings or patterns in unlabeled data, leveraging algorithms like k-means or hierarchical clustering. Opt for regression when predicting a continuous outcome based on labeled input features, applying models such as linear regression or polynomial regression to estimate relationships between variables.
Clustering Infographic
 libterm.com
libterm.com