Understanding the concept of limits is essential in calculus, as it describes the behavior of a function as it approaches a specific point. Mastering limits allows you to analyze continuity, derivatives, and integrals effectively. Explore the rest of this article to deepen your knowledge of limits and their vital role in mathematics.
Table of Comparison
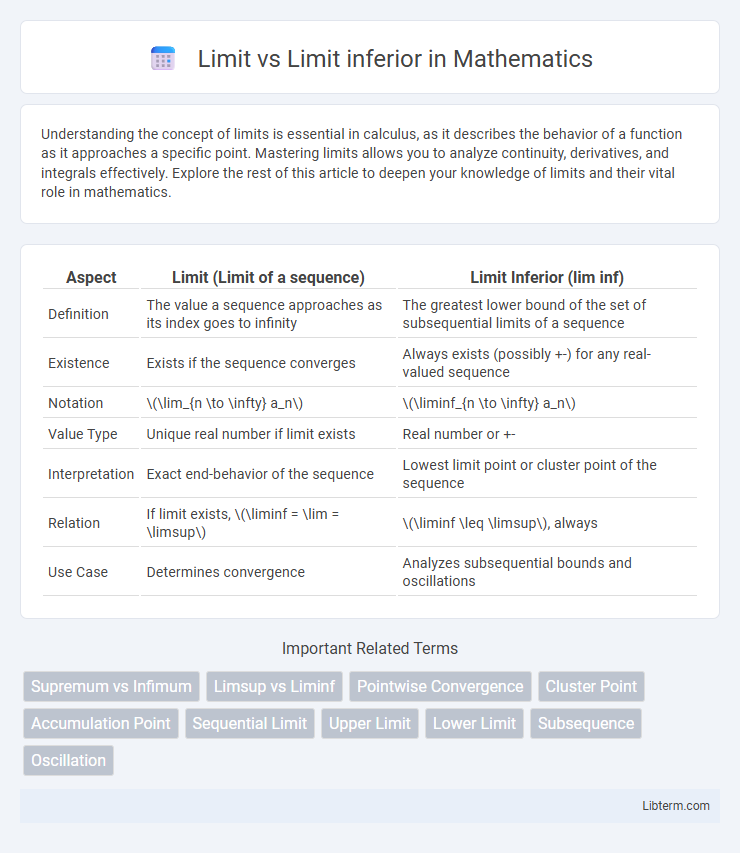
| Aspect | Limit (Limit of a sequence) | Limit Inferior (lim inf) |
|---|---|---|
| Definition | The value a sequence approaches as its index goes to infinity | The greatest lower bound of the set of subsequential limits of a sequence |
| Existence | Exists if the sequence converges | Always exists (possibly +-) for any real-valued sequence |
| Notation | \(\lim_{n \to \infty} a_n\) | \(\liminf_{n \to \infty} a_n\) |
| Value Type | Unique real number if limit exists | Real number or +- |
| Interpretation | Exact end-behavior of the sequence | Lowest limit point or cluster point of the sequence |
| Relation | If limit exists, \(\liminf = \lim = \limsup\) | \(\liminf \leq \limsup\), always |
| Use Case | Determines convergence | Analyzes subsequential bounds and oscillations |
Introduction to Limit and Limit Inferior
Limit of a sequence refers to the single value that the terms of the sequence approach as the index goes to infinity, capturing the precise behavior of convergence. Limit inferior, or lim inf, identifies the greatest lower bound of the subsequential limits, reflecting the smallest value that subsequences cluster around infinitely often. Understanding limit inferior is crucial for analyzing bounded sequences that do not converge, providing insight into their limiting behavior.
Fundamental Concepts Defined
Limit of a sequence represents the unique value that the terms approach as the index goes to infinity, provided it exists. Limit inferior (lim inf) defines the greatest lower bound of the set of subsequential limits, capturing the smallest accumulation point of the sequence. These fundamental concepts distinguish between overall convergence and the behavior of subsequences, essential in real analysis and measure theory.
Mathematical Notation and Formal Definitions
Limit of a sequence \( \{x_n\} \) is denoted by \( \lim_{n \to \infty} x_n = L \) if for every \( \epsilon > 0 \), there exists \( N \in \mathbb{N} \) such that \( |x_n - L| < \epsilon \) for all \( n \geq N \). The limit inferior, or \( \liminf_{n \to \infty} x_n \), is defined as the greatest lower bound of the set of subsequential limits, formally \( \liminf_{n \to \infty} x_n = \lim_{n \to \infty} \inf_{k \geq n} x_k \). The key difference is that the limit requires convergence to a single value, whereas the limit inferior captures the lowest accumulation point of the sequence through nested infimum operations.
Key Differences: Limit vs Limit Inferior
The key difference between limit and limit inferior lies in their definitions and applications in sequences. A limit of a sequence exists if the terms converge to a single value, while the limit inferior represents the greatest lower bound of the set of subsequential limits, capturing the "long-term floor" of the sequence's behavior. Limit inferior is especially useful for sequences that do not converge but exhibit oscillatory or bounded behavior, distinguishing it from the classical limit concept.
Properties of Limits
Limit describes the value a sequence or function approaches as the input tends to a point, ensuring uniqueness if it exists and satisfying the squeeze theorem for bounded sequences. Limit inferior, or lim inf, represents the greatest lower bound of subsequential limits and is always less than or equal to the limit when it exists. Both concepts adhere to monotonicity in sequences, with limit inferior serving as a tool to analyze convergence when limits fail to exist or oscillate.
Properties of Limit Inferior
The limit inferior of a sequence, denoted as lim inf, is the greatest lower bound of its subsequential limits, capturing the minimal cluster point where the sequence stabilizes from below. It is always less than or equal to the limit superior (lim sup) and provides important insights into the convergence behavior of bounded sequences, particularly when the actual limit does not exist. Key properties include monotonicity under subsequences, stability under limit operations, and its role as the infimum of tail suprema of the sequence.
Examples Illustrating Limits
The limit of a sequence captures its value as it approaches a specific point, such as \(\lim_{n \to \infty} \frac{1}{n} = 0\), while the limit inferior represents the greatest lower bound of subsequential limits, for example, the sequence \( (-1)^n + \frac{1}{n} \) has limit inferior \(-1\). In cases like \(a_n = \sin(n)\), the limit does not exist but the limit inferior is \(-1\), indicating the lowest cluster point of the sequence. These examples demonstrate how limits provide precise convergence values, whereas limit inferior offers insight into the asymptotic minimal behavior in oscillating or non-convergent sequences.
Examples Demonstrating Limit Inferior
The limit inferior (lim inf) of a sequence is the greatest lower bound of the set of subsequential limits, often illustrated by sequences that oscillate, such as \(a_n = (-1)^n + \frac{1}{n}\) where the lim inf is \(-1\), representing the lowest accumulation point. Another example is the sequence \(b_n = \frac{\sin(n)}{n}\), where the limit inferior equals zero because the sine function oscillates between \(-1\) and \(1\) while the divisor \(n\) grows without bound, pushing terms toward zero. These examples highlight how limit inferior captures the asymptotic minimal behavior of the sequence, even when the traditional limit does not exist or differs.
Practical Applications in Analysis
Limit and limit inferior play crucial roles in real analysis, especially in studying the behavior of sequences and functions. The limit provides the exact value a sequence converges to, essential for continuity and differentiability assessments, while the limit inferior offers a lower bound on subsequential limits, useful in optimization and stability analyses. Practical applications include evaluating the convergence of iterative algorithms, bounding error terms in numerical methods, and identifying accumulation points in signal processing.
Conclusion: Importance in Mathematical Analysis
Limit and limit inferior are crucial in mathematical analysis for understanding sequence behavior where traditional limits may not exist. Limit inferior provides a lower bound for the subsequential limits, ensuring insights into oscillatory and non-convergent sequences. This distinction enhances rigor in convergence criteria, measure theory, and real analysis, enabling precise characterization of limits and continuity.
Limit Infographic
 libterm.com
libterm.com