The Jacobian matrix plays a crucial role in vector calculus by representing all first-order partial derivatives of a vector-valued function. It is essential in transforming coordinates, analyzing system stability, and optimizing solutions in engineering and physics. Explore the rest of the article to understand how the Jacobian impacts your mathematical computations and practical applications.
Table of Comparison
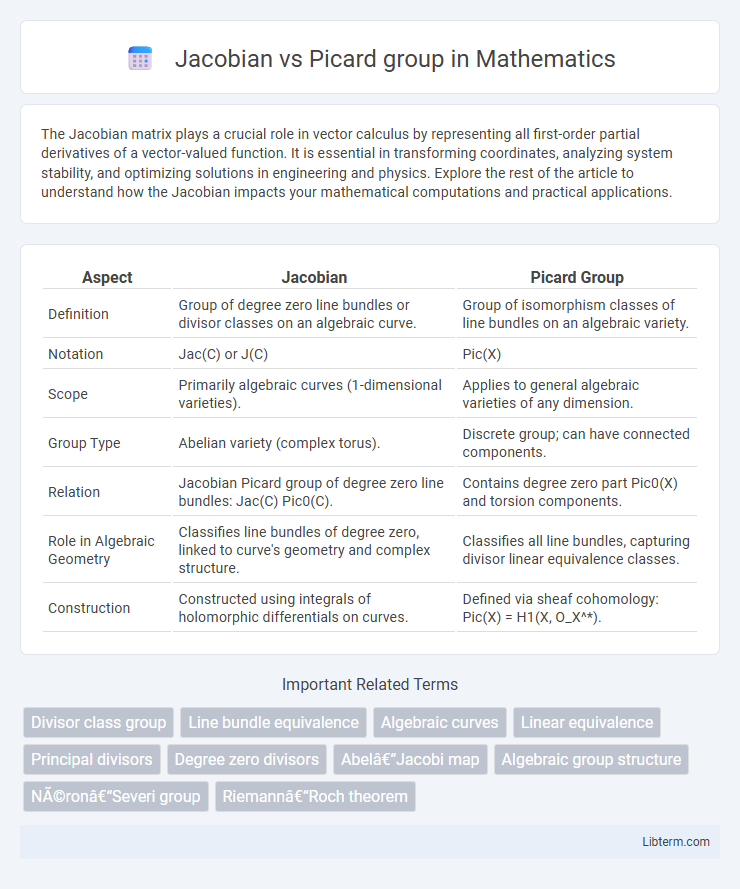
| Aspect | Jacobian | Picard Group |
|---|---|---|
| Definition | Group of degree zero line bundles or divisor classes on an algebraic curve. | Group of isomorphism classes of line bundles on an algebraic variety. |
| Notation | Jac(C) or J(C) | Pic(X) |
| Scope | Primarily algebraic curves (1-dimensional varieties). | Applies to general algebraic varieties of any dimension. |
| Group Type | Abelian variety (complex torus). | Discrete group; can have connected components. |
| Relation | Jacobian Picard group of degree zero line bundles: Jac(C) Pic0(C). | Contains degree zero part Pic0(X) and torsion components. |
| Role in Algebraic Geometry | Classifies line bundles of degree zero, linked to curve's geometry and complex structure. | Classifies all line bundles, capturing divisor linear equivalence classes. |
| Construction | Constructed using integrals of holomorphic differentials on curves. | Defined via sheaf cohomology: Pic(X) = H1(X, O_X^*). |
Introduction to Jacobian and Picard Groups
The Jacobian group of an algebraic curve parametrizes equivalence classes of degree zero divisors, forming an abelian variety that plays a central role in algebraic geometry and number theory. The Picard group generalizes this concept by classifying line bundles or divisor classes on a variety, capturing the global geometric and arithmetic properties of the underlying space. Understanding the interplay between the Jacobian and Picard groups is essential for studying divisors, line bundles, and their connections to complex tori and moduli spaces.
Historical Background and Development
The Jacobian variety, introduced by Bernhard Riemann in the 19th century, originally served as a tool for analyzing complex algebraic curves through their period matrices and theta functions. The Picard group, named after Emile Picard, emerged from the study of divisor classes and line bundles, capturing algebraic equivalence on algebraic varieties and playing a crucial role in the classification of algebraic surfaces. Over time, both concepts evolved to interconnect deeply within algebraic geometry, with the Jacobian often realized as a moduli space of line bundles, fundamentally linking geometric intuition with abstract algebraic structures.
Fundamental Definitions and Concepts
The Jacobian of a smooth projective algebraic curve is an abelian variety that parameterizes degree zero line bundles, effectively classifying divisor classes of degree zero on the curve. The Picard group, denoted Pic(X) for a variety X, is the group of isomorphism classes of line bundles on X, corresponding to divisor classes modulo linear equivalence. While the Jacobian focuses specifically on degree zero line bundles and has a natural structure as an algebraic group, the Picard group encompasses line bundles of all degrees and serves as a fundamental tool in the classification of line bundles and divisors on algebraic varieties.
The Jacobian Group: Structure and Properties
The Jacobian group of an algebraic curve, defined as the group of degree-zero divisor classes modulo linear equivalence, forms a complex torus with the structure of an abelian variety, enabling rich geometric and arithmetic analysis. It captures the curve's intrinsic geometry through its points representing line bundles, while its dimension equals the genus of the curve, linking topological and algebraic features. The Jacobian's group law, derived from the linear equivalence of divisors, plays a central role in number theory and algebraic geometry, distinguishing it fundamentally from the Picard group, which accounts for all line bundles without the degree-zero restriction.
The Picard Group: Structure and Properties
The Picard group of an algebraic variety classifies line bundles or divisor classes up to linear equivalence, forming an abelian group under tensor product. Its structure reflects key geometric properties, such as the Neron-Severi group quotient and the classification of algebraic cycles. Unlike the Jacobian, which parametrizes degree zero line bundles on curves, the Picard group applies to higher-dimensional varieties and encodes rich information about their divisor theory and cohomology.
Similarities Between Jacobian and Picard Groups
Both the Jacobian and Picard groups classify line bundles on algebraic curves, with the Jacobian representing degree-zero line bundles and the Picard group encompassing all line bundles up to isomorphism. Each group forms an abelian variety that reflects the geometric and arithmetic structure of the curve. Their isomorphism is established through the correspondence between divisors mod linear equivalence and line bundles, highlighting the deep link in algebraic geometry.
Key Differences: Jacobian vs Picard Group
The Jacobian of an algebraic curve is an abelian variety representing degree zero line bundles, while the Picard group classifies all line bundles modulo isomorphism, including those of varying degrees. The Picard group is typically a larger, more comprehensive object containing the Jacobian as the identity component that parameterizes line bundles of degree zero. Key differences include the Jacobian's focus on degree zero line bundles with an algebraic group structure versus the Picard group's broader classification encompassing all line bundles and divisors, often lacking a natural group variety structure.
Applications in Algebraic Geometry
The Jacobian of an algebraic curve classifies degree-zero line bundles and serves as a key tool in the study of abelian varieties, moduli spaces, and the theory of divisors. The Picard group extends this concept by capturing all line bundles up to isomorphism, providing a richer structure that encodes information about divisors of arbitrary degree and their algebraic equivalence classes. Both structures play a crucial role in understanding the geometry and arithmetic of varieties, enabling the study of morphisms, automorphisms, and the construction of moduli spaces in algebraic geometry.
Computational Aspects and Practical Examples
The Jacobian of an algebraic curve represents degree-zero line bundles and serves as a complex torus facilitating explicit computations in algebraic geometry, while the Picard group encodes all line bundles up to isomorphism, including varying degrees, making it more comprehensive but computationally intensive. Algorithms for the Jacobian, such as point addition using divisor class groups, enable efficient implementations in cryptography, for instance in hyperelliptic curve cryptosystems. Practical examples include computing the Jacobian of elliptic curves where group operations have polynomial-time complexity, contrasted with Picard groups in higher genus curves that require advanced techniques like Riemann-Roch space computations and often rely on symbolic algebra systems for effective handling.
Conclusion and Future Directions
The Jacobian variety and Picard group serve as fundamental constructs in algebraic geometry, with the Jacobian representing degree-zero line bundles and the Picard group encompassing all line bundles modulo isomorphism. Ongoing research explores deeper connections between these entities through the lens of moduli spaces, arithmetic geometry, and non-abelian generalizations. Future directions include leveraging advances in derived algebraic geometry and mirror symmetry to extend the understanding of their interplay and applications in modern mathematical physics.
Jacobian Infographic
 libterm.com
libterm.com