A module is a self-contained unit within a software system designed to perform a specific function or group of related functions, enabling better organization and maintainability of code. It allows developers to reuse code efficiently and simplifies debugging by isolating different parts of the program. Explore the rest of the article to understand how incorporating modules can improve your software development process.
Table of Comparison
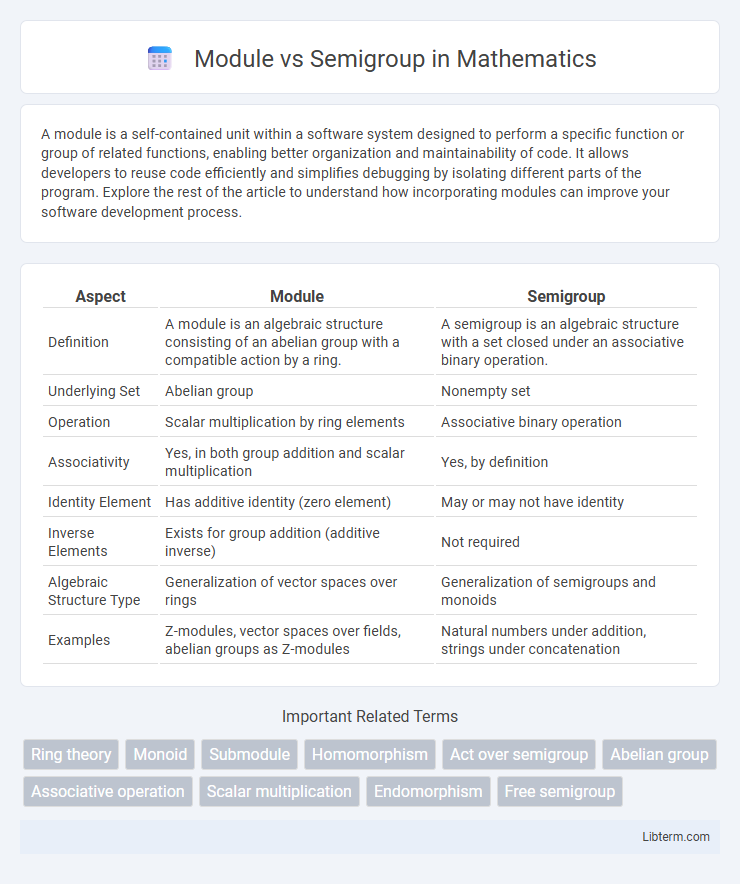
| Aspect | Module | Semigroup |
|---|---|---|
| Definition | A module is an algebraic structure consisting of an abelian group with a compatible action by a ring. | A semigroup is an algebraic structure with a set closed under an associative binary operation. |
| Underlying Set | Abelian group | Nonempty set |
| Operation | Scalar multiplication by ring elements | Associative binary operation |
| Associativity | Yes, in both group addition and scalar multiplication | Yes, by definition |
| Identity Element | Has additive identity (zero element) | May or may not have identity |
| Inverse Elements | Exists for group addition (additive inverse) | Not required |
| Algebraic Structure Type | Generalization of vector spaces over rings | Generalization of semigroups and monoids |
| Examples | Z-modules, vector spaces over fields, abelian groups as Z-modules | Natural numbers under addition, strings under concatenation |
Introduction to Modules and Semigroups
Modules generalize vector spaces by allowing scalars from a ring instead of a field, encompassing structures where addition and scalar multiplication coexist under ring actions. Semigroups consist of a set equipped with an associative binary operation, emphasizing closure and associativity without necessarily having an identity or inverses. Understanding modules involves studying abelian group structures with compatible ring actions, whereas semigroup theory centers on associativity within sets, providing foundational concepts in algebraic systems.
Fundamental Definitions: Module vs Semigroup
A module is an algebraic structure consisting of an abelian group equipped with a scalar multiplication by elements from a ring, satisfying distributive and associative properties. A semigroup is a set equipped with a single associative binary operation without necessarily having an identity element or inverses. Modules generalize vector spaces over rings, while semigroups focus solely on the associative operation without additive or scalar multiplication structures.
Algebraic Structures: Key Differences
Modules generalize vector spaces by allowing scalars from a ring rather than a field, providing a broader algebraic structure that supports addition and scalar multiplication. Semigroups consist solely of a set equipped with an associative binary operation, lacking additive inverses or scalar multiplication. The key difference lies in modules' richer operation set and compatibility requirements with ring elements, while semigroups focus only on closure and associativity under one operation.
Properties of Modules
Modules generalize vector spaces by allowing scalars from a ring instead of a field, resulting in richer algebraic structures. Key properties of modules include closure under addition and scalar multiplication, existence of additive identity and inverses, and distributivity of scalar multiplication over both ring addition and module addition. Unlike semigroups, modules require an Abelian group structure on the underlying set and compatibility conditions aligning ring actions with module operations.
Properties of Semigroups
Semigroups are algebraic structures consisting of a set equipped with an associative binary operation, ensuring closure and associativity but lacking an identity element or inverses. Unlike modules, semigroups do not require scalar multiplication or additive structure, focusing solely on the single associative operation. Key properties of semigroups include the presence of idempotent elements, Green's relations that classify elements based on divisibility, and the potential for embedding into monoids through adjoining identity elements.
Module Theory: Core Concepts
A module is an algebraic structure consisting of an abelian group equipped with a scalar multiplication by elements of a ring, generalizing vector spaces over fields. In contrast, a semigroup is a set equipped with an associative binary operation, lacking the richness of additive inverses and scalar multiplication present in modules. Module theory focuses on understanding modules over rings, including submodules, homomorphisms, and exact sequences, which extend concepts from linear algebra to more general algebraic settings.
Semigroup Theory: Core Concepts
Semigroup theory studies algebraic structures consisting of a set equipped with an associative binary operation, emphasizing the closure and associativity properties without requiring identity or invertibility. In contrast, modules extend the concept of vector spaces by allowing scalars from a ring instead of a field, incorporating additive group structures and scalar multiplication that satisfies distributivity and compatibility axioms. Understanding semigroups provides foundational insights into algebraic operations and morphisms, while modules facilitate the exploration of linear algebraic concepts over more general rings.
Applications of Modules in Mathematics
Modules generalize vector spaces by allowing scalars from a ring instead of a field, making them essential in abstract algebra and number theory. They facilitate the study of linear algebraic structures over rings, enabling applications in homological algebra, representation theory, and algebraic geometry. Modules provide a framework for analyzing solutions to systems of linear equations in more general settings, including module homomorphisms and exact sequences.
Applications of Semigroups in Mathematics
Semigroups, algebraic structures with an associative binary operation, find extensive applications across various mathematical domains such as automata theory, functional analysis, and combinatorics. Their utility in modeling transformation semigroups simplifies the study of state machines and language recognition, while in functional analysis, strongly continuous semigroups provide a framework for solving evolution equations. Unlike modules that generalize vector spaces over rings, semigroups emphasize operational closure and associativity, making them essential for problems involving iterative processes and system dynamics.
Comparative Analysis: Module vs Semigroup
Modules generalize vector spaces by allowing scalar multiplication over a ring rather than a field, providing richer algebraic structures compared to semigroups, which only require an associative binary operation without identities or inverses. Semigroups lack an additive structure and scalar multiplication, limiting their algebraic complexity relative to modules that combine additive abelian group properties with compatible ring actions. This fundamental difference makes modules central in module theory and homological algebra, while semigroups form a broader class studied in semigroup theory focused on operation composition.
Module Infographic
 libterm.com
libterm.com