Absolute clarity in communication eliminates misunderstandings and ensures your message is received exactly as intended. This concept applies across various fields, including mathematics, ethics, and technology, where precision is paramount. Discover how absolute principles impact your daily decisions and professional practices in the rest of this article.
Table of Comparison
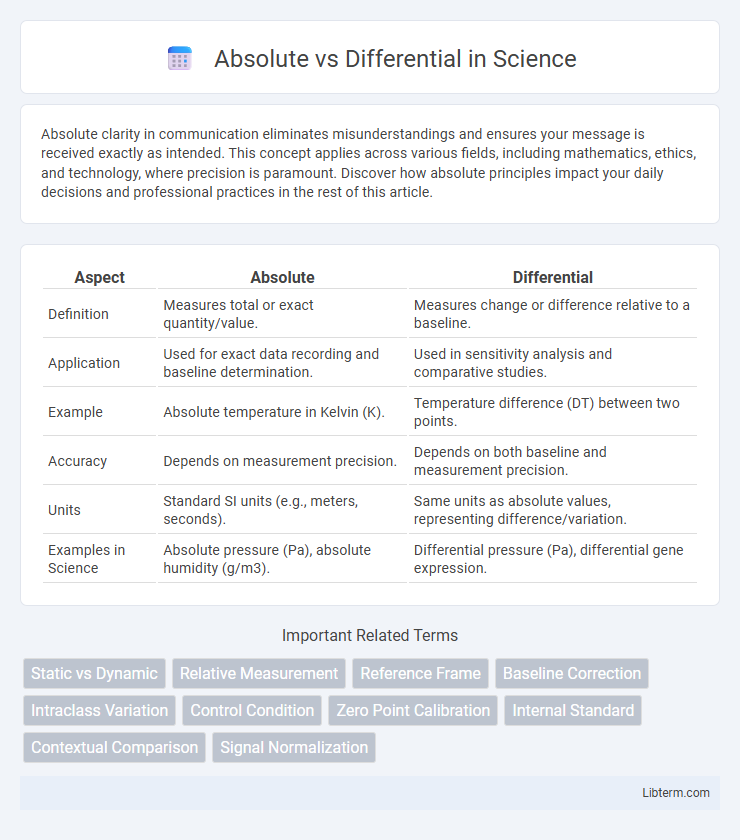
| Aspect | Absolute | Differential |
|---|---|---|
| Definition | Measures total or exact quantity/value. | Measures change or difference relative to a baseline. |
| Application | Used for exact data recording and baseline determination. | Used in sensitivity analysis and comparative studies. |
| Example | Absolute temperature in Kelvin (K). | Temperature difference (DT) between two points. |
| Accuracy | Depends on measurement precision. | Depends on both baseline and measurement precision. |
| Units | Standard SI units (e.g., meters, seconds). | Same units as absolute values, representing difference/variation. |
| Examples in Science | Absolute pressure (Pa), absolute humidity (g/m3). | Differential pressure (Pa), differential gene expression. |
Introduction to Absolute vs Differential
Absolute measurement provides a fixed reference point representing the total value from a known zero baseline, essential for applications like temperature or pressure sensing. Differential measurement captures the difference between two variables or points, often used in situations requiring detection of changes or gradients, such as flow rate or strain gauges. Understanding the distinction between absolute and differential measurement types is critical for selecting appropriate sensors and ensuring accurate data interpretation in engineering and scientific fields.
Defining Absolute Measurements
Absolute measurements provide exact values based on a reference standard, ensuring consistent and reproducible data across different contexts and instruments. These measurements quantify properties such as length, mass, or temperature using fixed units like meters, kilograms, and kelvins, enabling universal comparison and calibration. Understanding absolute measurements is essential in science and industry for maintaining accuracy and establishing baseline standards.
Understanding Differential Measurements
Differential measurements compare two input signals to determine their difference, reducing noise and improving accuracy in sensor readings. Unlike absolute measurements that reference a fixed point, differentials capture changes relative to another value, making them essential in applications like strain gauge sensors and differential amplifiers. Understanding this method enhances precision in electronic circuits by minimizing environmental interference and offset errors.
Key Differences between Absolute and Differential
Absolute measurement represents a value in relation to a fixed zero point, providing an exact quantification without reference to other values. Differential measurement records the difference between two variable points, highlighting relative changes or variations rather than fixed quantities. Key differences include absolute measurements offering fixed, consistent data, while differential measurements emphasize dynamic changes and comparative analysis.
Real-world Applications of Absolute Measurements
Absolute measurements provide exact values referenced from fixed standards, making them crucial in fields like meteorology for determining precise temperature and pressure readings essential to weather forecasting. In healthcare, absolute measurements enable accurate dosage calculations and vital sign assessments, ensuring patient safety and effective treatment outcomes. Industrial manufacturing relies on absolute measurements to maintain quality control through exact dimensions and tolerances, minimizing defects and optimizing product performance.
Practical Uses of Differential Measurements
Differential measurements are essential in practical applications such as sensor calibration, where comparing changes relative to a reference improves accuracy and noise reduction. Industries rely on differential techniques in strain gauges and temperature sensors to detect minute variations that absolute measurements might miss. This approach enhances precision monitoring in fields like engineering diagnostics and biomedical instrumentation.
Advantages of Absolute Methods
Absolute methods provide precise and direct measurements by referencing a fixed standard, eliminating cumulative errors common in differential techniques. This approach enhances accuracy in applications such as temperature calibration and pressure sensing, where exact baseline values are critical. Utilizing absolute methods reduces the need for frequent recalibration, improving reliability and consistency in analytical and industrial processes.
Benefits of Differential Approaches
Differential approaches offer enhanced precision by measuring changes relative to a baseline, reducing errors caused by environmental fluctuations and sensor drift. These methods improve accuracy in applications such as signal processing, navigation, and instrumentation by focusing on relative differences rather than absolute values. This results in more reliable and stable measurements, particularly in dynamic or noisy environments.
Challenges in Absolute vs Differential Analysis
Challenges in absolute vs differential analysis primarily arise from the precision and context sensitivity required for each method. Absolute analysis demands accurate baseline references and can be affected by measurement errors or environmental variations, while differential analysis faces challenges in isolating meaningful changes amidst noise and maintaining consistency across comparative data sets. Both approaches require robust calibration and validation protocols to ensure reliable and interpretable results in scientific and engineering applications.
Choosing between Absolute and Differential Methods
Choosing between absolute and differential methods depends on the precision requirements and environmental conditions of the measurement task. Absolute methods provide direct measurements with reference to a fixed standard, offering high accuracy in stable environments, while differential methods measure relative changes or differences, enhancing sensitivity and noise reduction in dynamic or noisy settings. Evaluating factors such as instrument calibration, response time, and application context ensures optimal method selection for reliable data acquisition.
Absolute Infographic
 libterm.com
libterm.com