Continuous integration enhances software development by automating code testing and integration, reducing errors and accelerating release cycles. This practice ensures consistent quality and allows teams to quickly identify and fix issues, improving overall project efficiency. Explore the rest of the article to understand how continuous integration can transform your development workflow.
Table of Comparison
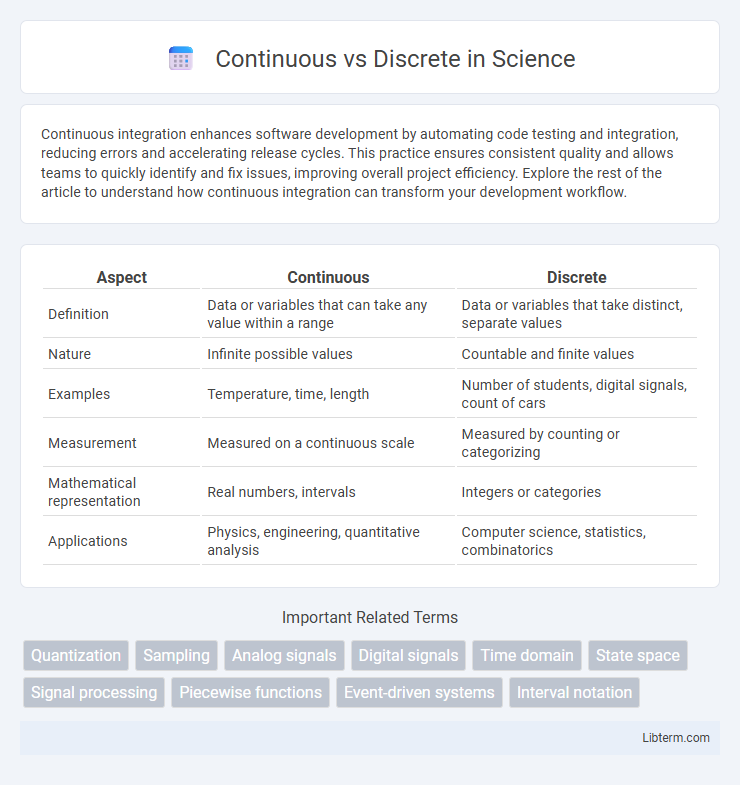
| Aspect | Continuous | Discrete |
|---|---|---|
| Definition | Data or variables that can take any value within a range | Data or variables that take distinct, separate values |
| Nature | Infinite possible values | Countable and finite values |
| Examples | Temperature, time, length | Number of students, digital signals, count of cars |
| Measurement | Measured on a continuous scale | Measured by counting or categorizing |
| Mathematical representation | Real numbers, intervals | Integers or categories |
| Applications | Physics, engineering, quantitative analysis | Computer science, statistics, combinatorics |
Understanding Continuous and Discrete Concepts
Continuous concepts represent data or phenomena that vary smoothly over a range without interruption, such as temperature or time, allowing for infinite possible values within an interval. Discrete concepts consist of distinct, separate values or categories, like the number of students or steps in a process, characterized by countable and often finite sets. Understanding the fundamental difference between continuous and discrete data is essential in fields like mathematics, statistics, and computer science for accurate modeling, analysis, and interpretation.
Key Definitions: Continuous vs Discrete
Continuous data represents values within an uninterrupted range, allowing for infinite possibilities between any two points, such as temperature or time. Discrete data consists of distinct, separate values that cannot be subdivided, often counted in whole numbers like the number of students or cars. Key distinctions lie in measurement precision and application, with continuous data supporting detailed analysis and discrete data suited for categorical or quantitative counting.
Real-World Examples of Continuous Data
Continuous data represents values on an infinite scale, such as temperature measurements fluctuating between 20.5degC and 21.7degC throughout the day or the varying heights of individuals in a population measured in centimeters. Examples include the precise weight of produce sold by grocery stores or the duration of phone calls recorded in seconds and fractions thereof. These real-world examples highlight continuous data's ability to assume any value within a specific range, enabling detailed analysis and fine-grained decision-making.
Practical Applications of Discrete Data
Discrete data is essential in computer science for algorithms and data structures, where values represent counts or categories such as network packets or user clicks. In inventory management, discrete quantities like product units enable precise stock control and demand forecasting. Healthcare relies on discrete data for patient records, diagnosis codes, and treatment outcomes, facilitating efficient data analysis and decision-making.
Differences in Data Representation
Continuous data represents information measured on an infinite scale, allowing any value within a range, such as temperature or time, while discrete data consists of distinct, separate values like counts of items or categories. Continuous data is typically represented using real numbers and can assume fractional values, whereas discrete data uses integers or labels with no intermediate values. In data visualization, continuous variables are often displayed with line graphs or histograms, while discrete variables are shown using bar charts or pie charts.
Mathematical Foundations of Continuous and Discrete
Continuous mathematics relies on concepts from calculus and real analysis, utilizing continuous variables and functions defined over infinite intervals, enabling the modeling of smooth phenomena through derivatives and integrals. Discrete mathematics studies countable, distinct structures such as integers, graphs, and finite sets, employing combinatorics, logic, and algebraic methods to analyze problems with indivisible elements. The mathematical foundations distinguish continuous systems governed by differential equations from discrete systems characterized by sequences, recurrences, and graph theory.
Visualization Techniques: Graphing Continuous and Discrete Data
Graphing continuous data typically involves line graphs or histograms that display data points connected smoothly, illustrating trends and patterns over a range. Discrete data visualization often uses bar charts or scatter plots with distinct, separate points that highlight individual categories or counts. Effective visualization depends on selecting techniques that accurately represent data types to convey clear, interpretable information.
Advantages and Limitations of Each Type
Continuous data allows for precise measurements and captures an infinite range of values, making it ideal for detailed analysis and trend identification. Its limitation lies in the complexity of data collection and the need for sophisticated tools to analyze vast amounts of granular information. Discrete data, characterized by distinct and separate values, simplifies data handling and is effective for counting and categorical classification but can miss subtle variations present in continuous data, limiting its use in fine-grained analysis.
Choosing Between Continuous and Discrete in Problem Solving
Choosing between continuous and discrete approaches in problem solving depends on the nature of the variables involved; continuous models apply to variables with infinite possible values within a range, such as time or temperature, while discrete models suit variables with distinct, separate values, like counts or categories. Continuous data analysis often requires calculus and differential equations, ideal for modeling smooth changes, whereas discrete data analysis uses combinatorics and finite algorithms for distinct event handling. Selecting the appropriate model significantly impacts accuracy and efficiency in fields like engineering, computer science, and statistics.
Summary: When to Use Continuous vs Discrete
Continuous data is ideal for measuring variables that can take any value within a range, such as temperature, time, or weight, allowing for detailed analysis and precise modeling. Discrete data suits scenarios involving countable, distinct categories or integers like the number of students, product defects, or survey responses, enabling clear classification and frequency analysis. Choosing between continuous and discrete depends on the nature of your variable and the level of granularity required for accurate data representation and decision-making.
Continuous Infographic
 libterm.com
libterm.com