Discrete data consists of distinct, separate values often used in counting objects or events, making it essential for categorical analysis in statistics. Understanding the characteristics of discrete variables helps you accurately interpret data sets and apply appropriate mathematical models. Explore the rest of the article to learn how discrete data impacts statistical analysis and decision-making processes.
Table of Comparison
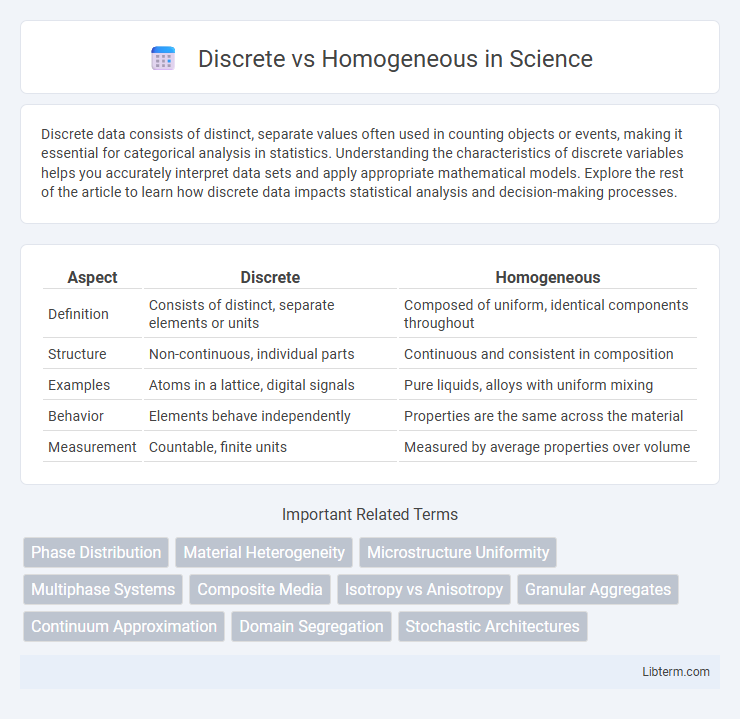
| Aspect | Discrete | Homogeneous |
|---|---|---|
| Definition | Consists of distinct, separate elements or units | Composed of uniform, identical components throughout |
| Structure | Non-continuous, individual parts | Continuous and consistent in composition |
| Examples | Atoms in a lattice, digital signals | Pure liquids, alloys with uniform mixing |
| Behavior | Elements behave independently | Properties are the same across the material |
| Measurement | Countable, finite units | Measured by average properties over volume |
Introduction to Discrete and Homogeneous Concepts
Discrete concepts refer to distinct, separate elements that can be individually counted or identified, often characterized by their finite or countably infinite nature. Homogeneous concepts involve elements that are uniform in composition or structure, exhibiting consistent properties throughout a system or dataset. Understanding the difference between discrete and homogeneous is fundamental in fields such as mathematics, physics, and computer science, where they influence data modeling, analysis, and problem-solving approaches.
Defining Discrete: Key Characteristics
Discrete data consists of distinct, separate values often counted as whole numbers, such as the number of students in a class or cars in a parking lot. Each value is isolated and cannot be meaningfully subdivided, highlighting its non-continuous nature. This contrasts with homogeneous data, which represents continuous measurements within a consistent category.
Understanding Homogeneous: Core Attributes
Homogeneous data consists of elements that share consistent, uniform characteristics or values within a dataset, enabling straightforward comparison and analysis. Core attributes of homogeneous data include uniform data types, consistent scales of measurement, and seamless integration without variation or segmentation. This uniformity facilitates efficient processing and reliable statistical modeling, making homogeneous datasets ideal for predictive analytics and quality control applications.
Discrete vs Homogeneous: Fundamental Differences
Discrete data consists of distinct, separate values often counted as integers or categories, while homogeneous data exhibits uniformity with consistent properties throughout a dataset. Discrete datasets are characterized by non-continuous, individually identifiable elements, whereas homogeneous datasets maintain similarity and lack variability across observations. Understanding these fundamental differences is crucial for selecting appropriate statistical methods and ensuring accurate data analysis.
Real-World Examples of Discrete Systems
Discrete systems are characterized by distinct, separate states or events that occur at specific points in time, such as traffic light sequences, digital communication protocols, and inventory management in warehouses. These systems rely on digital signals, binary data, or countable events, enabling precise control and analysis in manufacturing lines, computer networks, and banking transactions. Real-world examples include automated teller machines (ATMs), barcode scanning systems, and turnstile counters at subway stations that process distinct, individual inputs and outputs.
Practical Applications of Homogeneous Structures
Homogeneous structures are extensively used in materials science and engineering due to their uniform properties, enabling predictable performance in manufacturing processes such as casting and 3D printing. In chemical engineering, homogeneous catalysts facilitate consistent reaction rates by providing a uniform phase, enhancing efficiency in industrial synthesis. These structures also underpin uniform electrical conductivity in semiconductor devices, crucial for reliable microelectronics performance.
Advantages and Limitations of Discrete Models
Discrete models offer precise representation of individual entities and events, making them ideal for systems with distinct states or populations such as queuing theory and network traffic analysis. Their advantage lies in the ability to capture stochastic behavior and temporal dynamics with high resolution, allowing for accurate simulations and scenario testing. Limitations include increased computational complexity and scalability issues when applied to large or continuous systems, as they require detailed state tracking and can become resource-intensive.
Benefits and Challenges of Homogeneous Models
Homogeneous models offer benefits such as simplified analysis and consistent behavior across all components, facilitating scalability and easier implementation in systems like chemical mixtures or material composites. Challenges include limited ability to capture heterogeneous or localized variations, reducing accuracy in complex real-world scenarios where discrete differences significantly impact outcomes. Effective use of homogeneous models demands balancing simplicity with the need for precision, often requiring supplemental approaches or hybrid modeling techniques.
Choosing Between Discrete and Homogeneous Approaches
Choosing between discrete and homogeneous approaches depends on the nature of the data and analysis objectives. Discrete models excel in handling distinct, separate elements such as categorical data or individual events, providing detailed granularity for classification and decision-making. Homogeneous models are ideal for continuous or uniformly distributed data, enabling smooth approximations and efficient processing in scenarios like fluid dynamics or material behavior simulations.
Conclusion: Summary and Future Perspectives
Discrete models offer precise representation of individual elements or events, making them ideal for systems with distinct states or entities, while homogeneous models assume uniformity and continuity, simplifying analysis of large-scale or averaged phenomena. The choice between discrete and homogeneous approaches depends on the specific system characteristics and research goals, balancing detail against computational tractability. Future perspectives highlight the integration of hybrid models combining discrete and homogeneous components to enhance accuracy and scalability in complex system simulations.
Discrete Infographic
 libterm.com
libterm.com