Parallel computing enhances processing speed by dividing tasks across multiple processors simultaneously, improving efficiency and performance in complex computations. This approach is essential for handling large datasets and running advanced simulations in scientific research and artificial intelligence. Explore the rest of this article to discover how parallel computing can optimize Your technological projects.
Table of Comparison
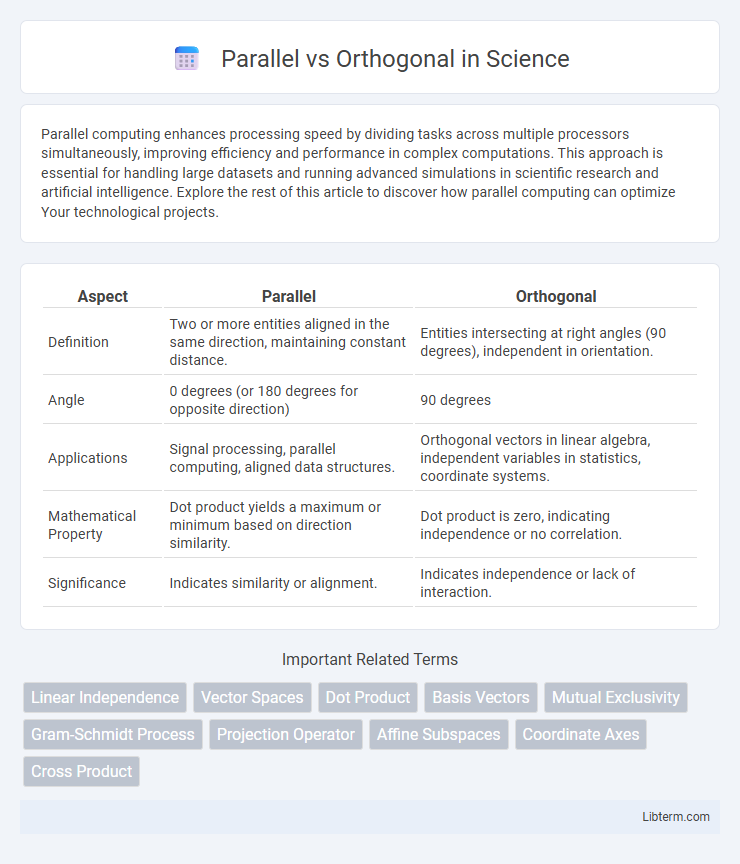
| Aspect | Parallel | Orthogonal |
|---|---|---|
| Definition | Two or more entities aligned in the same direction, maintaining constant distance. | Entities intersecting at right angles (90 degrees), independent in orientation. |
| Angle | 0 degrees (or 180 degrees for opposite direction) | 90 degrees |
| Applications | Signal processing, parallel computing, aligned data structures. | Orthogonal vectors in linear algebra, independent variables in statistics, coordinate systems. |
| Mathematical Property | Dot product yields a maximum or minimum based on direction similarity. | Dot product is zero, indicating independence or no correlation. |
| Significance | Indicates similarity or alignment. | Indicates independence or lack of interaction. |
Introduction to Parallel and Orthogonal Concepts
Parallel concepts involve elements aligned in the same direction or having similar attributes, enabling simultaneous processing or equivalent functionality in various contexts such as computing, geometry, and design. Orthogonal concepts refer to elements that are independent or perpendicular to each other, ensuring minimal interaction or interference, which is crucial in fields like programming, signal processing, and mathematics. Understanding the distinction between parallel and orthogonal principles aids in optimizing system architectures, enhancing modularity, and improving performance across technical and scientific disciplines.
Defining Parallelism in Geometry and Beyond
Parallel lines in geometry are defined as lines in the same plane that never intersect, maintaining a constant distance apart. Beyond geometry, parallelism extends to computer science, describing simultaneous processing tasks that run independently without interaction. This concept underpins modern computing architectures and algorithms, optimizing performance through concurrent execution.
Understanding Orthogonality: A Multifaceted Perspective
Orthogonality in mathematics and computer science denotes independence and non-interference, where orthogonal elements do not affect each other's outcomes, ensuring modularity and clarity in design. Unlike parallelism, which involves simultaneous execution or alignment, orthogonality emphasizes conceptual separation and minimal overlap in functionality or data. This multifaceted perspective enables robust system architecture by simplifying debugging, enhancing scalability, and promoting reusable components.
Key Differences Between Parallel and Orthogonal
Parallel lines run in the same direction and never intersect, maintaining a constant distance between them, while orthogonal lines meet at a right angle (90 degrees), representing perpendicularity. In vector spaces, parallel vectors have proportional components, whereas orthogonal vectors have a dot product of zero, indicating no directional similarity. These distinctions are critical in fields such as geometry, computer graphics, and signal processing, where orientation and interaction of lines or vectors determine structural and functional properties.
Applications of Parallelism Across Disciplines
Parallelism enhances computational efficiency in disciplines like computer science, facilitating faster algorithm execution through simultaneous processing. In linguistics, parallel structures improve textual coherence and readability, aiding language learning and translation applications. Engineering leverages orthogonal design to separate concerns, ensuring system components operate independently for robust and maintainable solutions.
Real-World Uses of Orthogonality
Orthogonality plays a critical role in engineering and computer science, enabling independent functionality and reducing interference between components, as seen in modular software design and error-correcting codes. In signal processing, orthogonal signals allow simultaneous transmission without cross-talk, optimizing bandwidth and communication clarity. These real-world applications demonstrate orthogonality's value in enhancing system efficiency and reliability across diverse technological domains.
Mathematical Representation: Parallel vs. Orthogonal
Parallel vectors have a mathematical representation where one vector is a scalar multiple of the other, expressed as v = k * w with scalar k 0, indicating they share the same or exact opposite direction. Orthogonal vectors are represented by the dot product equaling zero, v * w = 0, which means the vectors are perpendicular and have no projection onto each other. These definitions are fundamental in linear algebra, geometry, and vector space analysis for defining directionality and independence.
Visualizing Parallel and Orthogonal Relationships
Parallel relationships in visualization emphasize elements aligning in the same direction, highlighting repetition or continuity, such as parallel lines in graphs or charts representing consistent trends. Orthogonal relationships showcase elements intersecting at right angles, clarifying independent variables or contrasting dimensions in data visualizations like scatter plots or bar charts. Effective visualization of parallel and orthogonal relationships enhances comprehension of spatial and conceptual connections within complex datasets.
Significance in Engineering and Technology
Parallel systems in engineering enable simultaneous processing, significantly boosting computational speed and efficiency, particularly in multi-core processors and parallel programming frameworks. Orthogonal designs ensure modularity and independence among system components, enhancing maintainability, scalability, and reducing cross-interference in complex architectures like signal processing and communication systems. The combination of parallelism for performance and orthogonality for clarity forms the backbone of advanced technological solutions in fields such as embedded systems and digital electronics.
Choosing Between Parallel and Orthogonal Approaches
Choosing between parallel and orthogonal approaches depends on the specific goals and constraints of a project. Parallel approaches execute multiple tasks simultaneously to maximize efficiency and reduce processing time, ideal for workloads with independent operations. Orthogonal approaches emphasize independence and minimal interference between components or variables, enhancing clarity and adaptability in complex systems where modularity is crucial.
Parallel Infographic
 libterm.com
libterm.com