Heap is a specialized tree-based data structure that efficiently manages prioritized data, supporting quick insertion, deletion, and retrieval of the highest (or lowest) element. Commonly used in algorithms like Dijkstra's shortest path and implementing priority queues, heaps ensure optimal performance through their unique properties such as the heap property and complete binary tree structure. Explore the rest of the article to discover how heaps can optimize your data processing tasks and improve algorithm efficiency.
Table of Comparison
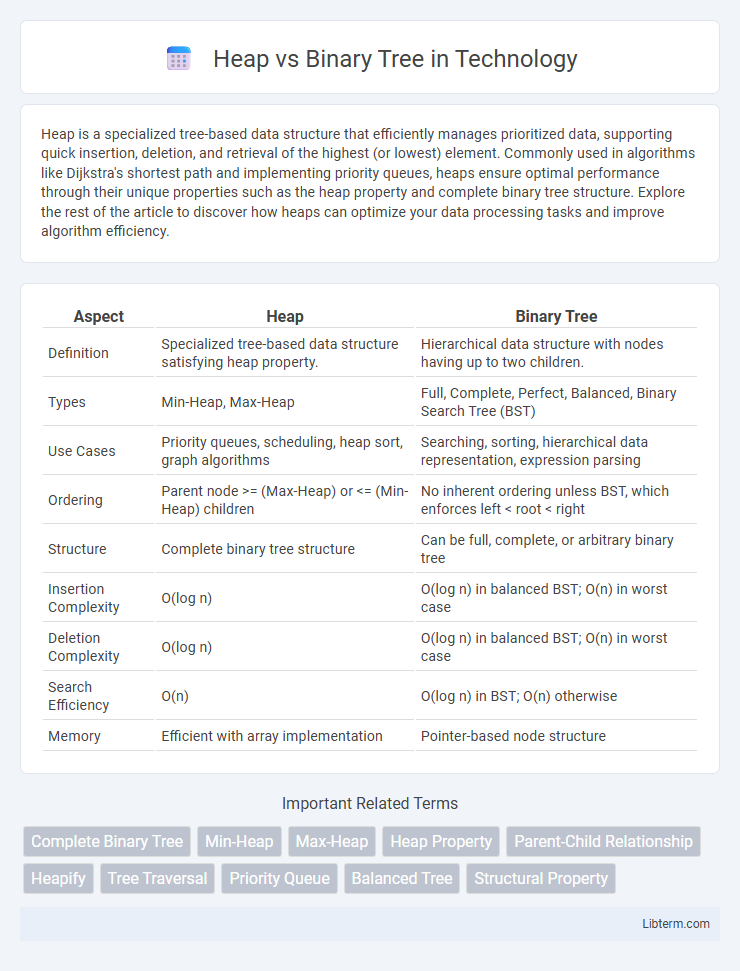
| Aspect | Heap | Binary Tree |
|---|---|---|
| Definition | Specialized tree-based data structure satisfying heap property. | Hierarchical data structure with nodes having up to two children. |
| Types | Min-Heap, Max-Heap | Full, Complete, Perfect, Balanced, Binary Search Tree (BST) |
| Use Cases | Priority queues, scheduling, heap sort, graph algorithms | Searching, sorting, hierarchical data representation, expression parsing |
| Ordering | Parent node >= (Max-Heap) or <= (Min-Heap) children | No inherent ordering unless BST, which enforces left < root < right |
| Structure | Complete binary tree structure | Can be full, complete, or arbitrary binary tree |
| Insertion Complexity | O(log n) | O(log n) in balanced BST; O(n) in worst case |
| Deletion Complexity | O(log n) | O(log n) in balanced BST; O(n) in worst case |
| Search Efficiency | O(n) | O(log n) in BST; O(n) otherwise |
| Memory | Efficient with array implementation | Pointer-based node structure |
Introduction to Heaps and Binary Trees
Heaps are specialized tree-based data structures that satisfy the heap property, where each parent node is either greater than or equal to (max-heap) or less than or equal to (min-heap) its child nodes, enabling efficient priority queue operations. Binary trees consist of nodes with up to two children, commonly used for searching, sorting, and hierarchical data representation, but they do not enforce a specific ordering constraint like heaps. The primary distinction lies in heaps being complete binary trees optimized for quick access to the highest or lowest priority element, while binary trees offer flexible structures for varied traversal and node arrangement patterns.
Defining Heap Data Structures
Heap data structures are specialized binary trees that maintain a specific ordering property, such as the max-heap property where each parent node is greater than or equal to its children, or the min-heap property where each parent node is smaller than or equal to its children. Unlike general binary trees, heaps are complete binary trees, meaning all levels are fully filled except possibly the last, which is filled from left to right. This structure supports efficient priority queue operations like insertion and extraction in logarithmic time.
Understanding Binary Trees
Binary trees are hierarchical data structures consisting of nodes, where each node has at most two children referred to as the left and right child. Understanding binary trees involves recognizing their use in organizing data for efficient searching, sorting, and hierarchical representation. Unlike heaps, binary trees do not enforce a strict ordering property between parent and child nodes, allowing more flexibility in structure but requiring different traversal methods such as inorder, preorder, and postorder to access data effectively.
Key Differences Between Heap and Binary Tree
Heaps are specialized binary trees that satisfy the heap property, where each parent node is either greater than or equal to (max-heap) or less than or equal to (min-heap) its child nodes, ensuring a specific order. Binary trees do not require such ordering, allowing any arrangement of node values without heap constraints. Unlike binary trees primarily used for hierarchical data representation, heaps are optimized for priority queue operations, providing efficient access to the maximum or minimum element.
Types of Heaps: Min-Heap vs Max-Heap
Min-Heaps maintain the smallest element at the root, ensuring that each parent node is less than or equal to its children, which optimizes priority queue operations like extracting the minimum value. Max-Heaps invert this structure by placing the largest element at the root, with each parent node greater than or equal to its children, making them ideal for algorithms requiring quick access to the maximum value. Unlike general binary trees, both Min-Heaps and Max-Heaps enforce strict ordering properties that enable efficient insertion, deletion, and heapify operations crucial for sorting and priority management tasks.
Binary Tree Variants and Use Cases
Binary tree variants include full, complete, perfect, and balanced binary trees, each optimized for specific structural properties and operational efficiency. Full and perfect binary trees are commonly used in heap implementations and efficient memory allocation, while balanced binary trees like AVL and Red-Black trees support dynamic set operations with guaranteed logarithmic time complexity. Use cases vary from expression parsing and sorting algorithms to database indexing and priority queues, where the choice of binary tree variant directly impacts performance and resource management.
Heap Operations and Applications
Heap operations primarily include insertion, deletion of the root (often the maximum or minimum element), and heapify, which maintains the heap property during these modifications. Heaps enable efficient priority queue implementations, as extracting the top-priority element or inserting new elements can be performed in O(log n) time. Common applications of heaps include algorithms like Dijkstra's shortest path, Huffman coding for data compression, and priority scheduling in operating systems.
Binary Tree Traversal Techniques
Binary tree traversal techniques include in-order, pre-order, and post-order methods, which systematically visit nodes for data processing or retrieval. In-order traversal accesses nodes in ascending order for binary search trees, while pre-order and post-order methods are used for tree construction and deletion tasks. These traversals differ from heap operations, where priority queue structures rely on specialized heapify processes instead of general traversal patterns.
Performance Comparison: Heap vs Binary Tree
Heap and binary tree structures differ significantly in performance, primarily due to their intended use cases and balancing mechanisms. Heaps offer efficient insertions and deletions with O(log n) time complexity, optimized for priority queue operations, while binary trees provide flexible data organization but may degrade to O(n) in unbalanced cases. Balanced binary trees like AVL or Red-Black Trees guarantee O(log n) lookups, insertions, and deletions, outperforming heaps in search operations but without the heap's priority-based ordering efficiency.
Choosing the Right Structure: Heap or Binary Tree?
Choosing the right data structure between a heap and a binary tree depends on the specific use case and performance requirements. Heaps are ideal for priority queue implementations due to their efficient O(log n) time complexity for insertions and deletions, especially in min-heaps and max-heaps, where the highest or lowest priority element is accessed quickly. Binary trees offer more flexibility in traversal and ordering but lack the guaranteed structural properties of heaps, making them suitable for search operations and representing hierarchical data without priority constraints.
Heap Infographic
 libterm.com
libterm.com