Sparsity refers to the condition where data or signals contain a significant number of zero or near-zero elements, making them efficiently representable using fewer resources. This property is crucial in fields like machine learning, signal processing, and compressed sensing, enabling faster computations and reduced storage requirements. Explore the rest of the article to uncover how sparsity can transform your data analysis and modeling approaches.
Table of Comparison
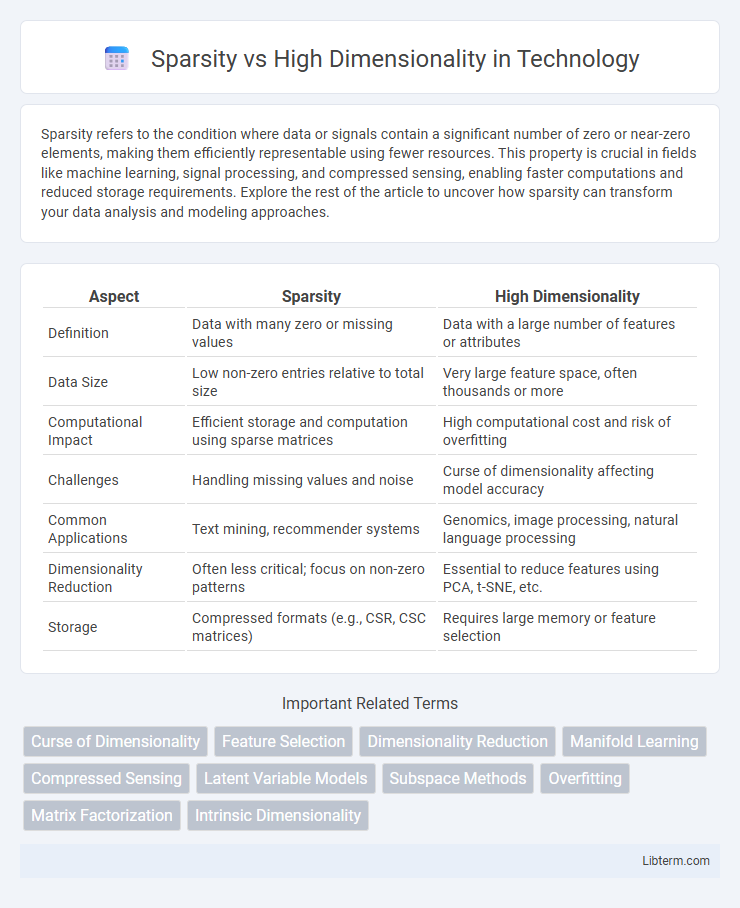
| Aspect | Sparsity | High Dimensionality |
|---|---|---|
| Definition | Data with many zero or missing values | Data with a large number of features or attributes |
| Data Size | Low non-zero entries relative to total size | Very large feature space, often thousands or more |
| Computational Impact | Efficient storage and computation using sparse matrices | High computational cost and risk of overfitting |
| Challenges | Handling missing values and noise | Curse of dimensionality affecting model accuracy |
| Common Applications | Text mining, recommender systems | Genomics, image processing, natural language processing |
| Dimensionality Reduction | Often less critical; focus on non-zero patterns | Essential to reduce features using PCA, t-SNE, etc. |
| Storage | Compressed formats (e.g., CSR, CSC matrices) | Requires large memory or feature selection |
Introduction to Sparsity and High Dimensionality
Sparsity refers to datasets or models where most elements are zero or insignificant, enabling efficient computation and storage. High dimensionality involves data with a large number of features or variables, often leading to challenges such as the curse of dimensionality and overfitting. Understanding the balance between sparsity and high dimensionality is crucial for developing scalable machine learning algorithms and improving model interpretability.
Defining Sparsity in Data Analysis
Sparsity in data analysis refers to datasets where the majority of elements are zero or absent, creating a distribution dominated by null or missing values. This characteristic significantly impacts algorithms, requiring specialized techniques to efficiently process and extract meaningful patterns. High dimensionality often exacerbates sparsity, as the expansion of feature space increases the likelihood of sparse representations, challenging traditional data analysis methods.
Understanding High Dimensionality
High dimensionality refers to datasets with a large number of features or variables, often leading to the "curse of dimensionality," where the volume of the feature space increases exponentially, making data analysis and pattern recognition challenging. High dimensional data can suffer from sparsity, where many features contain little relevant information or are zero-valued, complicating machine learning model training and increasing computational complexity. Techniques such as dimensionality reduction, feature selection, and regularization are essential to efficiently process and extract meaningful insights from high dimensional datasets.
Key Differences Between Sparse and High-Dimensional Data
Sparse data is characterized by a large proportion of zero or null values, often found in datasets with high dimensionality but emphasizing the lack of meaningful entries. High-dimensional data involves a vast number of features or variables, which can lead to computational challenges such as the curse of dimensionality, regardless of data density. The key difference lies in sparsity indicating data emptiness within dimensions, while high dimensionality refers to the sheer number of features, each affecting analysis and modeling strategies differently.
Challenges Posed by Sparsity
Sparsity in high-dimensional data causes challenges such as increased computational complexity and reduced model accuracy due to the abundance of zero or missing values. Sparse datasets often lead to overfitting, as machine learning algorithms struggle to find meaningful patterns in limited non-zero observations. Handling sparsity requires advanced techniques like regularization, dimensionality reduction, and specialized algorithms to improve performance and interpretability.
Complications of High Dimensional Spaces
High dimensional spaces often suffer from the "curse of dimensionality," where data points become sparse, making distance metrics less meaningful and degrading the performance of machine learning models. The exponential increase in volume causes computational challenges and requires more data to reliably estimate parameters, leading to overfitting and increased model complexity. Effective dimensionality reduction techniques, such as PCA or t-SNE, are essential to mitigate these issues by capturing the most informative features while preserving data structure.
Applications Leveraging Sparse and High-Dimensional Data
Applications leveraging sparse and high-dimensional data excel in fields like natural language processing, computer vision, and bioinformatics, where datasets often contain vast features but only a few relevant signals. Techniques such as sparse coding, Lasso regression, and principal component analysis reduce dimensionality while preserving essential information, enhancing interpretability and computational efficiency. These methods enable robust pattern recognition and predictive modeling in scenarios with limited observations amidst large feature spaces.
Techniques for Managing Sparsity
Techniques for managing sparsity in high-dimensional data include dimensionality reduction methods such as Principal Component Analysis (PCA) and t-Distributed Stochastic Neighbor Embedding (t-SNE), which transform data into lower-dimensional spaces while preserving essential structure. Regularization techniques like L1 (Lasso) promote sparsity in model parameters, effectively reducing complexity and enhancing interpretability. Additionally, matrix factorization and embedding methods are employed to reconstruct sparse data representations, improving computational efficiency and predictive performance in machine learning tasks.
Approaches to Handle High Dimensionality
Techniques to handle high dimensionality include dimensionality reduction methods like Principal Component Analysis (PCA) and t-Distributed Stochastic Neighbor Embedding (t-SNE), which transform data into lower-dimensional spaces while preserving significant features. Feature selection algorithms such as LASSO and Recursive Feature Elimination (RFE) identify and retain the most informative variables to improve model performance and interpretability. Sparse coding and regularization techniques promote models that emphasize essential features and reduce noise, effectively addressing the challenges posed by high-dimensional datasets.
Future Directions in Sparse and High-Dimensional Data Research
Future research in sparsity and high-dimensional data focuses on developing scalable algorithms that efficiently handle massive datasets with numerous features while maintaining interpretability. Advances in machine learning models such as sparse deep learning networks and dimensionality reduction techniques aim to improve predictive accuracy and computational efficiency. Integration of domain-specific knowledge and quantum computing may further revolutionize the processing and analysis of sparse high-dimensional data.
Sparsity Infographic
 libterm.com
libterm.com