A Binary Search Tree (BST) is a data structure that stores elements in a sorted manner, allowing efficient search, insertion, and deletion operations. Each node in a BST has at most two children, with the left child containing values less than the parent and the right child containing values greater than the parent. Discover how implementing a BST can optimize your data handling by reading the full article.
Table of Comparison
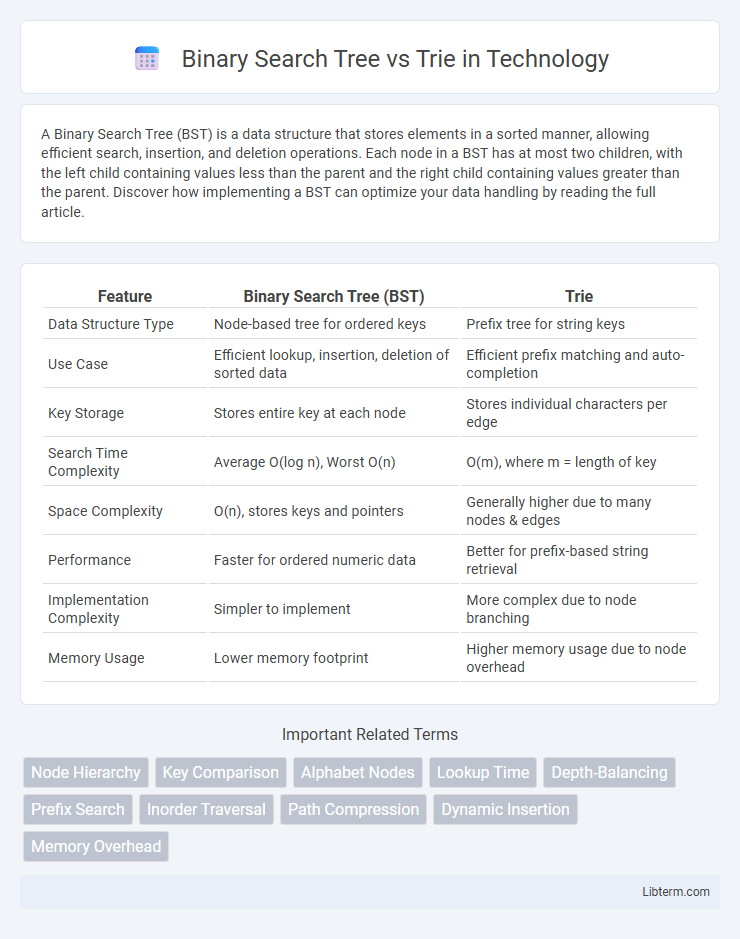
| Feature | Binary Search Tree (BST) | Trie |
|---|---|---|
| Data Structure Type | Node-based tree for ordered keys | Prefix tree for string keys |
| Use Case | Efficient lookup, insertion, deletion of sorted data | Efficient prefix matching and auto-completion |
| Key Storage | Stores entire key at each node | Stores individual characters per edge |
| Search Time Complexity | Average O(log n), Worst O(n) | O(m), where m = length of key |
| Space Complexity | O(n), stores keys and pointers | Generally higher due to many nodes & edges |
| Performance | Faster for ordered numeric data | Better for prefix-based string retrieval |
| Implementation Complexity | Simpler to implement | More complex due to node branching |
| Memory Usage | Lower memory footprint | Higher memory usage due to node overhead |
Introduction to Binary Search Tree and Trie
A Binary Search Tree (BST) organizes data hierarchically, where each node contains a key, and left subtree keys are smaller while right subtree keys are larger, enabling efficient search, insertion, and deletion operations in average O(log n) time. A Trie, or prefix tree, stores keys as paths from the root to leaves, optimizing prefix-based searches with each node representing a character, commonly used in applications like autocomplete and spell checking. Both structures improve search efficiency, but BSTs excel in ordered data retrieval, whereas Tries are specialized for dynamic prefix matching.
Structure and Node Representation
Binary Search Trees (BSTs) organize nodes with a single key value, where each node contains pointers to at most two child nodes, maintaining order based on key comparisons for efficient search, insertion, and deletion. Tries, or prefix trees, represent nodes as arrays or hash maps mapping characters to child nodes, with each node storing partial keys, enabling fast retrieval of strings by common prefixes. BST nodes are typically structured with key, left child, and right child fields, whereas Trie nodes contain arrays or maps of child pointers along with flags to indicate complete words or keys.
Data Storage Differences
Binary Search Trees (BST) store data in nodes containing keys with left and right child pointers, organizing values based on key comparisons for efficient search, insertion, and deletion, ideal for ordered data. Tries, or prefix trees, store data in a multi-way tree structure where each node represents a character or part of a key, enabling fast retrieval of strings by common prefixes, optimized for associative arrays with string keys. While BSTs store data as discrete nodes with key values, Tries encode data by paths and node links, resulting in a trade-off between memory usage and search speed depending on the dataset's nature.
Insertion and Deletion Operations
Insertion in a Binary Search Tree (BST) involves comparing values and traversing left or right until the correct leaf position is found, with an average time complexity of O(log n) but worst-case O(n) in unbalanced trees. Trie insertion requires iterating through each character of the key, creating node paths if absent, consistently offering O(m) time complexity, where m is the key length. Deletion in BST can be complex, often involving node replacement by in-order predecessor or successor to maintain tree properties, while Trie deletion requires careful removal of nodes only when they are no longer prefixes for other keys, preserving existing key paths efficiently.
Search Efficiency Comparison
Binary Search Trees (BST) provide efficient average-case search times of O(log n) when balanced, but their worst-case search time can degrade to O(n) due to skewed structures. Tries guarantee search times proportional to the length of the key, O(m), independent of the number of keys, making them highly efficient for prefix-based searches and large datasets with common prefixes. While BSTs excel in range queries and ordered data retrieval, tries outperform BSTs in scenarios requiring fast, character-level key lookups and autocomplete functions.
Space Complexity Analysis
Binary Search Trees (BST) typically require O(n) space, storing nodes with pointers to left and right children, where n represents the number of elements. Tries consume more space, often O(ALPHABET_SIZE * LENGTH * n), due to storing multiple child pointers for each character per node, where ALPHABET_SIZE represents the character set size and LENGTH is the maximum key length. While BSTs are more space-efficient for sparse datasets, Tries become beneficial for quick prefix searches despite higher memory usage.
Use Cases and Applications
Binary Search Trees (BSTs) excel in dynamic datasets requiring ordered data retrieval, such as database indexing and range queries, offering efficient average-case search, insertion, and deletion operations in O(log n) time. Tries are ideal for prefix-based search tasks, including autocomplete systems, spell checkers, and IP routing, enabling fast retrieval of strings by their prefixes with time complexity proportional to the key length. While BSTs prioritize balanced structure for quick comparative operations, Tries optimize for character-level access patterns, making them suitable for applications heavily reliant on lexical data processing.
Pros and Cons of Binary Search Tree
A Binary Search Tree (BST) offers efficient average-case search, insertion, and deletion operations with O(log n) time complexity, making it suitable for dynamic data sets requiring ordered traversal. However, its performance degrades to O(n) in the worst case when the tree becomes unbalanced, leading to inefficient operations. BSTs consume less memory compared to Tries, as they do not require additional nodes for each character, but they lack the prefix-based search optimization that Tries provide for string keys.
Pros and Cons of Trie
Trie offers fast retrieval and prefix matching, making it ideal for autocomplete and spell-check applications, with search time complexity proportional to the key length rather than the number of keys. Its memory consumption can be high due to storing multiple pointers for each node, which presents scalability challenges for large datasets. Unlike binary search trees that handle ordered data efficiently, tries excel in handling strings but require more intricate implementation and larger space overhead.
Choosing Between BST and Trie
Choosing between a Binary Search Tree (BST) and a Trie depends on the specific application and data characteristics. BSTs provide efficient search, insertion, and deletion for sorted data with average time complexity of O(log n), ideal for dynamic datasets with variable keys. Tries offer faster retrieval for prefix-based searches and are optimal for storing large sets of strings with common prefixes, operating in O(m) time where m is key length.
Binary Search Tree Infographic
 libterm.com
libterm.com