Suffix trees provide efficient solutions for string processing tasks by representing all suffixes of a given text in a compressed trie form. They enable rapid pattern matching, substring search, and finding longest common substrings with time complexity advantages over naive methods. Explore the rest of the article to understand how suffix trees can optimize your text processing challenges.
Table of Comparison
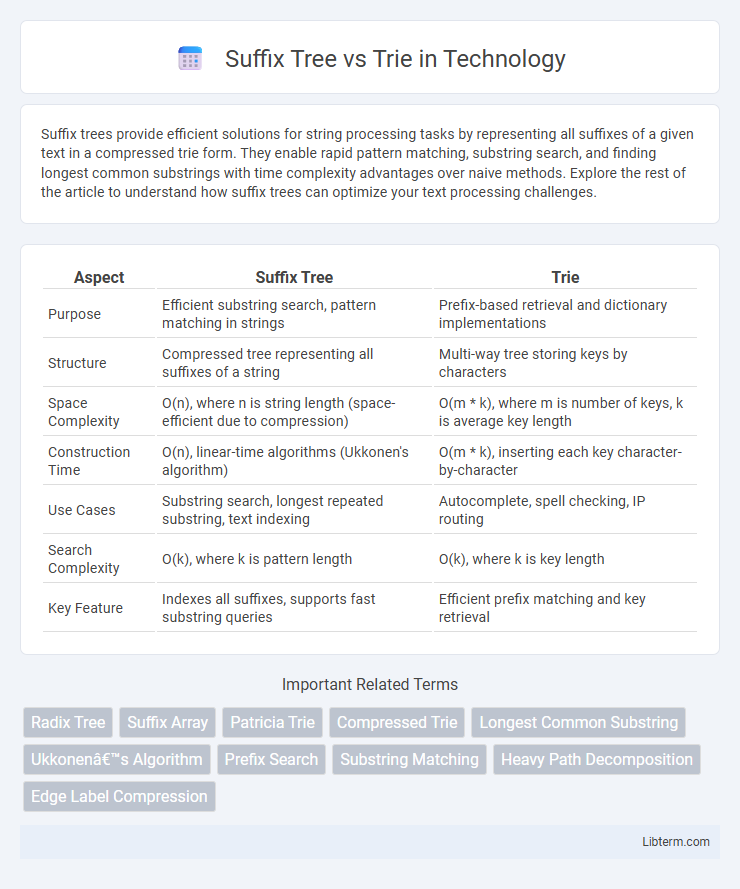
| Aspect | Suffix Tree | Trie |
|---|---|---|
| Purpose | Efficient substring search, pattern matching in strings | Prefix-based retrieval and dictionary implementations |
| Structure | Compressed tree representing all suffixes of a string | Multi-way tree storing keys by characters |
| Space Complexity | O(n), where n is string length (space-efficient due to compression) | O(m * k), where m is number of keys, k is average key length |
| Construction Time | O(n), linear-time algorithms (Ukkonen's algorithm) | O(m * k), inserting each key character-by-character |
| Use Cases | Substring search, longest repeated substring, text indexing | Autocomplete, spell checking, IP routing |
| Search Complexity | O(k), where k is pattern length | O(k), where k is key length |
| Key Feature | Indexes all suffixes, supports fast substring queries | Efficient prefix matching and key retrieval |
Introduction to Suffix Trees and Tries
Suffix trees are specialized data structures that represent all suffixes of a given string, enabling efficient pattern matching and substring search with linear-time complexity. Tries, also known as prefix trees, store collections of keys by organizing common prefixes to optimize retrieval operations, especially in dictionary and autocomplete implementations. While tries handle prefix-based queries efficiently, suffix trees excel at solving complex problems related to suffixes and substring analysis in strings.
Core Concepts: What is a Suffix Tree?
A suffix tree is a compressed trie structure that represents all suffixes of a given string, allowing efficient pattern matching and substring search. Each edge in a suffix tree is labeled with a substring, enabling linear-time complexity for various string operations like finding longest repeated substrings and identifying common substrings between sequences. Key applications include bioinformatics, text indexing, and data compression due to their space-efficient representation and fast query performance compared to standard tries.
Understanding the Trie Data Structure
The Trie data structure, also known as a prefix tree, organizes strings by storing common prefixes in shared nodes, enabling efficient searching, insertion, and prefix matching operations. Each node represents a character, and paths from the root to leaf nodes correspond to stored strings, optimizing retrieval tasks in applications like autocomplete and spell checking. Unlike suffix trees, which index all suffixes of a string and focus on substring queries, tries excel at handling collections of keys with fast prefix-based lookups.
Construction Algorithms: Suffix Tree vs Trie
Suffix tree construction algorithms like Ukkonen's algorithm achieve linear-time complexity O(n) by incrementally building the tree and utilizing suffix links to efficiently handle repetitions in the input string. In contrast, trie construction involves inserting each word character by character, resulting in O(m * k) time complexity, where m is the number of words and k is the length of the longest word. Suffix trees are more complex to build but provide powerful substring search capabilities, while tries offer straightforward and efficient prefix-based search structures.
Space Complexity Comparison
Suffix trees typically consume more space than tries due to their more complex structure, storing not just nodes but entire suffixes with edge labels representing substrings, leading to O(n) space complexity but with a high constant factor. Tries, representing prefixes of a set of strings with single-character edges, generally have a simpler structure and may use less space, approximately O(m * s) where m is the total length of all strings and s is the alphabet size. The space overhead in suffix trees arises from explicit storage of suffix links and compressed edges, whereas tries allocate nodes for each character, influencing their respective scalability in memory usage.
Time Complexity in Search Operations
Suffix trees enable fast substring search operations with a time complexity of O(m), where m is the length of the query string, due to their compact representation of all suffixes of a text. Tries, on the other hand, perform search operations in O(m) time as well, but they generally consume more space since they represent entire prefixes rather than suffixes. In practical applications, suffix trees are preferred for complex substring searches over large texts because they provide enhanced efficiency and scalability compared to tries.
Use Cases: When to Use Suffix Trees
Suffix trees excel in string-matching applications requiring fast substring searches, such as DNA sequence analysis, plagiarism detection, and data compression algorithms like Lempel-Ziv. They enable efficient pattern discovery, longest repeated substring identification, and rapid substring presence testing in linear time relative to the input size. Use suffix trees when large-scale genome sequencing data or extensive text corpora necessitate quick and repeated substring queries and complex pattern matching tasks.
Applications of Tries in Computing
Tries are widely used in computing for efficient retrieval of strings, such as word search in dictionaries and autocomplete features. Their structure allows fast prefix matching, making them ideal for IP routing table lookups and spell-checking applications. Unlike suffix trees, tries excel in scenarios requiring quick access to keys and support of dynamic insertions and deletions.
Pros and Cons: Suffix Tree vs Trie
Suffix trees provide efficient substring search and pattern matching with a linear-time construction, making them ideal for complex string algorithms; however, they require significant memory space and are more complicated to implement. Tries offer faster insert and prefix search operations with simpler structure and lower memory usage for smaller alphabets but can become inefficient for large datasets or lengthy input strings due to increased depth and redundant storage. Choosing between suffix trees and tries depends on the specific application requirements for speed, memory, and scalability in string processing tasks.
Conclusion: Choosing the Right Data Structure
Suffix trees excel in solving complex string problems like substring search, pattern matching, and bioinformatics tasks due to their efficient representation of all suffixes of a text. Tries provide effective prefix-based retrieval, making them ideal for dictionary implementations and autocomplete systems where memory usage is a concern. Selecting between suffix tree and trie depends on the specific application requirements: suffix trees offer faster substring queries at the cost of higher space complexity, while tries deliver simpler prefix searches with more compact storage.
Suffix Tree Infographic
 libterm.com
libterm.com