Average Value at Risk (AVaR) provides a comprehensive measure of potential losses by averaging the tail-end risks beyond a specified confidence level. It captures the expected shortfall, offering a more informative risk assessment compared to the standard Value at Risk (VaR) metric. Explore the article to understand how AVaR can enhance Your financial risk management strategies.
Table of Comparison
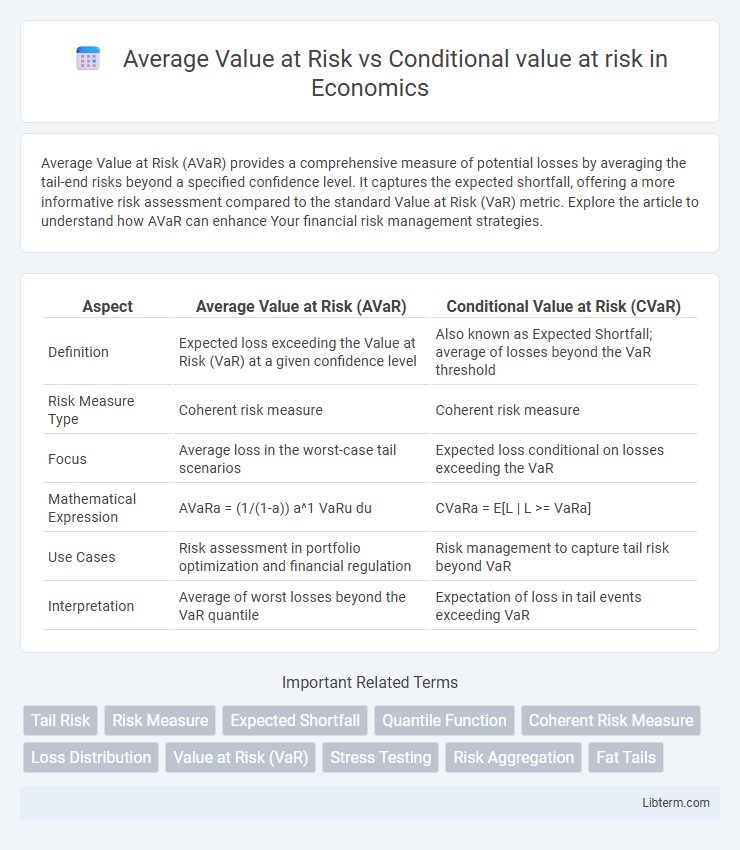
| Aspect | Average Value at Risk (AVaR) | Conditional Value at Risk (CVaR) |
|---|---|---|
| Definition | Expected loss exceeding the Value at Risk (VaR) at a given confidence level | Also known as Expected Shortfall; average of losses beyond the VaR threshold |
| Risk Measure Type | Coherent risk measure | Coherent risk measure |
| Focus | Average loss in the worst-case tail scenarios | Expected loss conditional on losses exceeding the VaR |
| Mathematical Expression | AVaRa = (1/(1-a)) a^1 VaRu du | CVaRa = E[L | L >= VaRa] |
| Use Cases | Risk assessment in portfolio optimization and financial regulation | Risk management to capture tail risk beyond VaR |
| Interpretation | Average of worst losses beyond the VaR quantile | Expectation of loss in tail events exceeding VaR |
Introduction to Risk Measures in Finance
Average Value at Risk (AVaR), also known as Conditional Value at Risk (CVaR), represents a coherent risk measure that estimates the expected loss exceeding a specified Value at Risk (VaR) threshold in financial portfolios. Unlike VaR, which identifies a cutoff loss level at a given confidence, CVaR provides insight into tail risk by averaging losses beyond that quantile, enhancing risk management and regulatory compliance. This distinction makes CVaR particularly valuable for assessing extreme market events and optimizing portfolio risk-adjusted returns.
Defining Average Value at Risk (AVaR)
Average Value at Risk (AVaR), also known as Expected Shortfall, quantifies the expected loss in the worst-case percentile of a portfolio's loss distribution beyond the Value at Risk (VaR) threshold. AVaR provides a coherent risk measure by accounting for the tail losses exceeding the VaR level, making it more sensitive to extreme risk scenarios compared to VaR alone. This risk metric is widely used in financial risk management for stress testing and regulatory capital estimation due to its ability to capture the severity of potential losses.
Understanding Conditional Value at Risk (CVaR)
Conditional Value at Risk (CVaR) quantifies the expected loss exceeding the Value at Risk (VaR) threshold, providing a more comprehensive risk assessment by focusing on tail-end losses. Unlike Average Value at Risk, which estimates potential losses at a given confidence level, CVaR captures the severity of extreme losses in the worst-case scenarios. This makes CVaR a crucial metric in financial risk management and portfolio optimization for understanding downside risk beyond simple VaR measures.
Mathematical Formulations of AVaR and CVaR
Average Value at Risk (AVaR) and Conditional Value at Risk (CVaR) are coherent risk measures used to assess tail risk in financial portfolios, with AVaR representing the expected loss given that losses exceed a specified Value at Risk (VaR) threshold. Mathematically, CVaR at confidence level \(\alpha\) is defined as \( \text{CVaR}_\alpha(X) = \frac{1}{1-\alpha} \int_\alpha^1 \text{VaR}_p(X) \, dp \), where \(X\) is the loss random variable and \(\text{VaR}_p(X)\) is the \(p\)-quantile of \(X\). AVaR can be expressed as an optimization problem: \(\text{AVaR}_\alpha(X) = \min_{u \in \mathbb{R}} \left( u + \frac{1}{1-\alpha} \mathbb{E}[(X - u)^+] \right)\), highlighting its use as a convex measure that generalizes CVaR by capturing expected tail losses beyond VaR.
Differences Between AVaR and CVaR
Average Value at Risk (AVaR) and Conditional Value at Risk (CVaR) both measure tail risk but differ in interpretation and calculation methods. AVaR calculates the expected loss exceeding a specified quantile, averaging all losses beyond the Value at Risk (VaR) threshold, while CVaR is often considered a coherent risk measure providing a more conservative and comprehensive assessment of extreme losses. The main difference lies in CVaR's ability to capture the full tail distribution beyond VaR, making it a preferred metric for risk-averse investors seeking to manage potential extreme financial risks effectively.
Applications of AVaR in Portfolio Management
Average Value at Risk (AVaR), also known as Conditional Value at Risk (CVaR), is widely applied in portfolio management to measure and control potential extreme losses beyond the Value at Risk (VaR) threshold. Portfolio managers utilize AVaR to optimize asset allocation by minimizing tail risk, enhancing risk-adjusted returns, and ensuring regulatory compliance under frameworks like Basel III. Its ability to capture the expected shortfall of losses makes AVaR a preferred tool for stress testing, scenario analysis, and robust risk budgeting in diversified investment portfolios.
Real-World Uses of CVaR in Risk Assessment
Conditional Value at Risk (CVaR) offers a more comprehensive risk assessment by measuring the expected losses beyond the Value at Risk (VaR) threshold, making it preferable for capturing tail risk in financial portfolios. CVaR is widely used in industries like banking, insurance, and energy trading to optimize capital allocation and enhance risk management strategies under extreme market conditions. Its ability to quantify potential losses in worst-case scenarios supports regulatory compliance and informs stress testing frameworks.
Advantages and Limitations: AVaR vs CVaR
Average Value at Risk (AVaR) offers a coherent risk measure that captures the expected losses beyond the Value at Risk (VaR) threshold, providing a more comprehensive assessment of tail risk compared to VaR alone. Conditional Value at Risk (CVaR), also known as Expected Shortfall, improves on AVaR by focusing explicitly on the tail distribution's average losses, enhancing risk sensitivity and regulatory compliance, especially under extreme market conditions. While AVaR's simplicity facilitates easier computational implementation, CVaR's ability to account for the severity of tail losses makes it more robust, though it may require more complex estimation techniques and larger data samples to achieve accurate risk quantification.
Regulatory Perspectives on AVaR and CVaR
Regulatory frameworks often prioritize Conditional Value at Risk (CVaR) due to its coherent risk measure properties and ability to capture tail risk more effectively compared to Average Value at Risk (AVaR). CVaR is favored in Basel III and Solvency II regulations for its sensitivity to extreme losses, enhancing capital adequacy assessments and risk management practices. Despite AVaR being used in some internal models, its regulatory acceptance is limited because CVaR provides a more comprehensive view of potential losses beyond the Value at Risk (VaR) threshold.
Choosing the Right Risk Metric for Your Needs
Average Value at Risk (VaR) estimates the maximum potential loss within a specific confidence level, making it suitable for quick, regulatory-focused assessments. Conditional Value at Risk (CVaR), or Expected Shortfall, provides a deeper analysis by measuring the average losses beyond the VaR threshold, capturing tail risk more comprehensively. Choosing between VaR and CVaR depends on your risk tolerance, regulatory requirements, and the need for precision in modeling extreme loss scenarios.
Average Value at Risk Infographic
 libterm.com
libterm.com