Ordinary Least Squares (OLS) is a fundamental statistical method used to estimate the parameters in a linear regression model by minimizing the sum of squared residuals between observed and predicted values. This technique ensures the best linear unbiased estimators when certain assumptions, like homoscedasticity and normality of errors, hold true. Explore the rest of the article to understand how OLS can improve your data analysis and modeling accuracy.
Table of Comparison
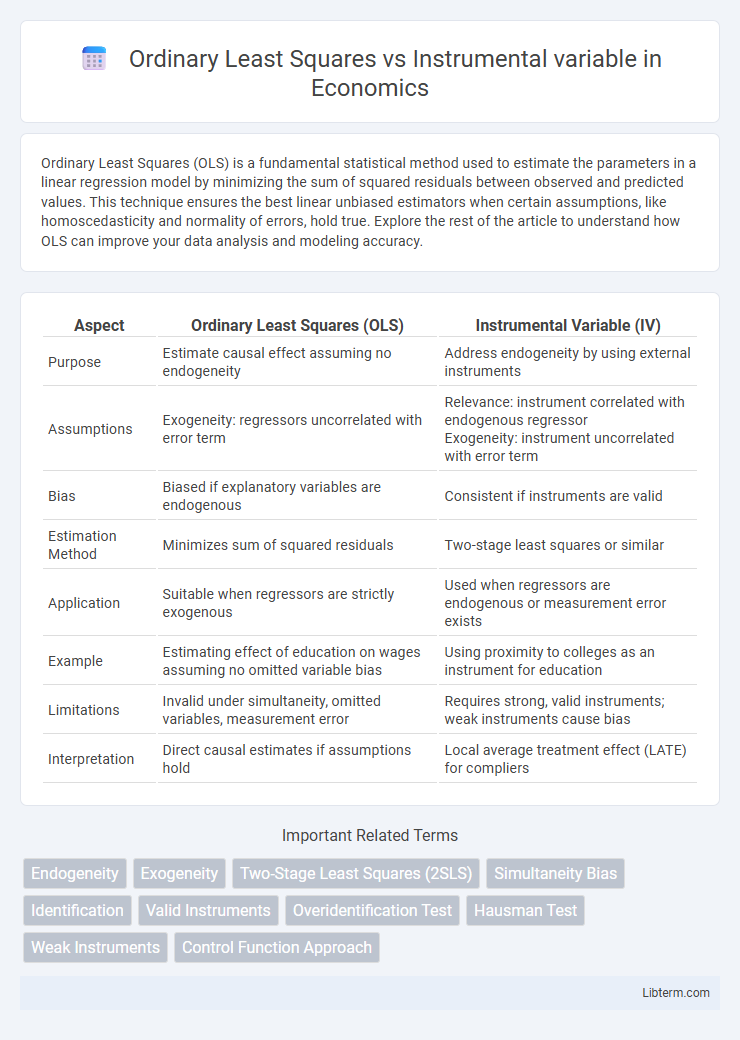
| Aspect | Ordinary Least Squares (OLS) | Instrumental Variable (IV) |
|---|---|---|
| Purpose | Estimate causal effect assuming no endogeneity | Address endogeneity by using external instruments |
| Assumptions | Exogeneity: regressors uncorrelated with error term | Relevance: instrument correlated with endogenous regressor Exogeneity: instrument uncorrelated with error term |
| Bias | Biased if explanatory variables are endogenous | Consistent if instruments are valid |
| Estimation Method | Minimizes sum of squared residuals | Two-stage least squares or similar |
| Application | Suitable when regressors are strictly exogenous | Used when regressors are endogenous or measurement error exists |
| Example | Estimating effect of education on wages assuming no omitted variable bias | Using proximity to colleges as an instrument for education |
| Limitations | Invalid under simultaneity, omitted variables, measurement error | Requires strong, valid instruments; weak instruments cause bias |
| Interpretation | Direct causal estimates if assumptions hold | Local average treatment effect (LATE) for compliers |
Introduction to Ordinary Least Squares (OLS)
Ordinary Least Squares (OLS) is a fundamental method in linear regression used to estimate the relationship between dependent and independent variables by minimizing the sum of squared residuals. OLS assumes that the regressors are exogenous, meaning no correlation exists between the explanatory variables and the error term, ensuring unbiased and consistent parameter estimates. However, when endogeneity or omitted variable bias arises, OLS estimates can become unreliable, prompting the use of alternative techniques like Instrumental Variables.
Fundamental Assumptions of OLS
Ordinary Least Squares (OLS) relies on key assumptions including linearity, no perfect multicollinearity, exogeneity, and homoscedasticity to produce unbiased and consistent estimates. The critical assumption of exogeneity requires that the explanatory variables be uncorrelated with the error term, ensuring no endogeneity bias. When this assumption is violated, Instrumental Variable (IV) estimation is employed to obtain consistent parameter estimates by using instruments correlated with the endogenous regressors but uncorrelated with the error term.
Understanding Instrumental Variables (IV)
Instrumental Variables (IV) address endogeneity issues in Ordinary Least Squares (OLS) by using instruments uncorrelated with the error term but correlated with the endogenous regressors. IV estimation provides consistent parameter estimates when OLS suffers from bias due to omitted variable bias, measurement error, or simultaneity. The validity of an instrument is crucial, requiring relevance (strong correlation with the endogenous variable) and exogeneity (no direct effect on the dependent variable except through the endogenous regressor).
Key Differences Between OLS and IV
Ordinary Least Squares (OLS) estimates causal relationships assuming no endogeneity, relying on the exogeneity of explanatory variables, while Instrumental Variables (IV) address endogeneity by using instruments correlated with the endogenous regressors but uncorrelated with the error term. OLS produces biased and inconsistent estimates when regressors correlate with the error term, but IV provides consistent estimates under valid instrument conditions. Key differences lie in the treatment of endogeneity, assumptions about error terms, and the reliance on external instruments for identification in IV.
When OLS Fails: The Problem of Endogeneity
Ordinary Least Squares (OLS) fails when endogeneity arises due to correlation between regressors and the error term, leading to biased and inconsistent estimates. Instrumental Variable (IV) methods address this problem by using instruments--variables correlated with the endogenous regressors but uncorrelated with the error term--to yield consistent parameter estimates. The validity and strength of the instruments are critical for IV estimation to overcome endogeneity in econometric models.
Role of Instruments in IV Estimation
Instrumental variables (IV) estimation addresses endogeneity issues in Ordinary Least Squares (OLS) by introducing instruments--variables correlated with the endogenous regressors but uncorrelated with the error term. These instruments isolate the exogenous variation needed to obtain consistent parameter estimates when OLS coefficients are biased and inconsistent. The validity of IV estimation hinges on the strength and relevance of the instruments, ensuring accurate identification of causal effects.
Step-by-Step: How IV Estimation Works
Instrumental Variable (IV) estimation addresses endogeneity by using instruments--variables correlated with the endogenous regressors but uncorrelated with the error term--to obtain consistent parameter estimates. The step-by-step IV process involves first regressing the endogenous variable on the instrument(s) to extract predicted values, then regressing the dependent variable on these predicted values to isolate causal effects. Unlike Ordinary Least Squares (OLS), which can produce biased estimates when regressors are endogenous, IV estimation provides consistent and unbiased estimates under valid instrument conditions.
Advantages and Limitations of OLS
Ordinary Least Squares (OLS) offers straightforward estimation of linear regression coefficients with minimum variance under the Gauss-Markov assumptions, providing unbiased and consistent estimates when explanatory variables are uncorrelated with the error term. Limitations arise in the presence of endogeneity caused by omitted variable bias, measurement error, or simultaneity, leading to biased and inconsistent OLS estimates. In such cases, Instrumental Variable (IV) methods are preferred as they provide consistent estimators by using instruments correlated with the endogenous regressors but uncorrelated with the error term, overcoming OLS limitations.
Strengths and Weaknesses of IV Techniques
Instrumental variable (IV) techniques address endogeneity issues that ordinary least squares (OLS) cannot, providing consistent estimates when explanatory variables correlate with the error term. IV methods require valid instruments that are strongly correlated with the endogenous regressors but uncorrelated with the error term, which can be challenging to identify and test. Weak instruments lead to biased IV estimates and reduce estimator precision, undermining the strength of IV methods despite their advantage in mitigating endogeneity.
Choosing Between OLS and IV: Practical Guidelines
Choosing between Ordinary Least Squares (OLS) and Instrumental Variables (IV) estimation depends primarily on the presence of endogeneity in the regression model. OLS provides unbiased and consistent estimates only when the regressors are exogenous, meaning no correlation with the error term; if endogeneity arises due to omitted variables, measurement error, or simultaneity, IV methods should be employed to obtain consistent estimates by using valid instruments correlated with the endogenous regressors but uncorrelated with the error term. Practical guidelines recommend testing for endogeneity using Hausman or Durbin-Wu-Hausman tests and ensuring the validity and strength of instruments through tests such as the Sargan-Hansen overidentification test and first-stage F-statistics before choosing IV over OLS.
Ordinary Least Squares Infographic
 libterm.com
libterm.com