The log-normal distribution describes a random variable whose logarithm is normally distributed, commonly used in finance, biology, and environmental science to model data with positive skewness. It accurately represents variables such as stock prices, income distribution, or particle sizes where values cannot be negative and tend to cluster at lower levels but have occasional large spikes. Explore the rest of the article to understand how the log-normal distribution can be applied to your data analysis and why it is important for modeling real-world phenomena.
Table of Comparison
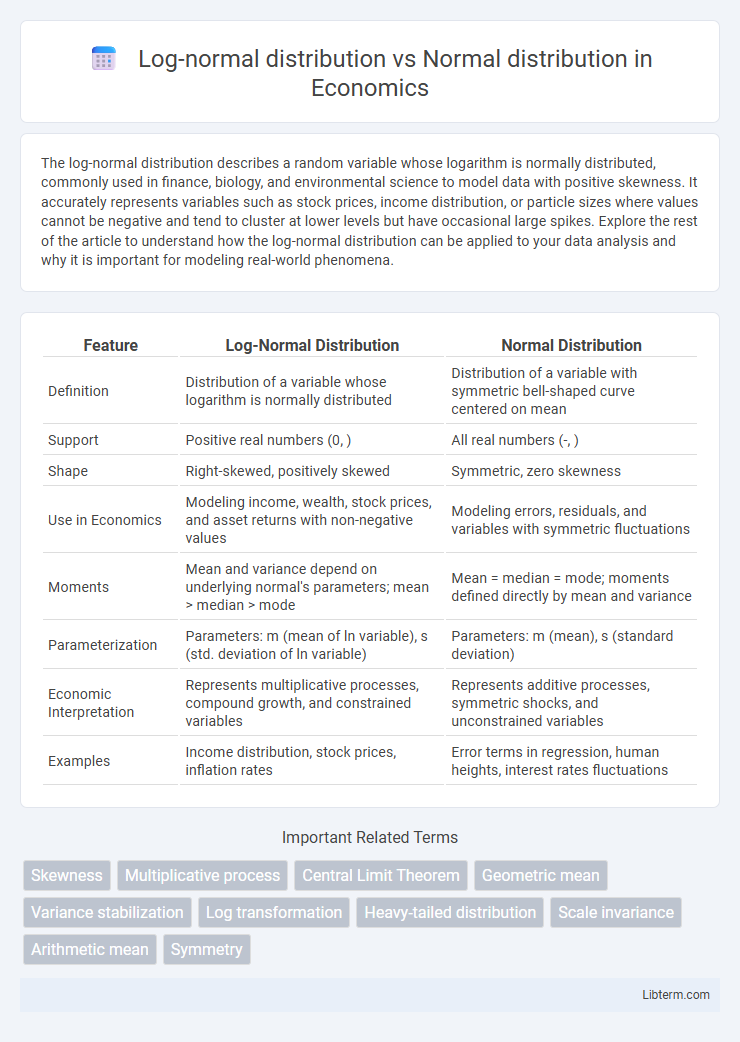
| Feature | Log-Normal Distribution | Normal Distribution |
|---|---|---|
| Definition | Distribution of a variable whose logarithm is normally distributed | Distribution of a variable with symmetric bell-shaped curve centered on mean |
| Support | Positive real numbers (0, ) | All real numbers (-, ) |
| Shape | Right-skewed, positively skewed | Symmetric, zero skewness |
| Use in Economics | Modeling income, wealth, stock prices, and asset returns with non-negative values | Modeling errors, residuals, and variables with symmetric fluctuations |
| Moments | Mean and variance depend on underlying normal's parameters; mean > median > mode | Mean = median = mode; moments defined directly by mean and variance |
| Parameterization | Parameters: m (mean of ln variable), s (std. deviation of ln variable) | Parameters: m (mean), s (standard deviation) |
| Economic Interpretation | Represents multiplicative processes, compound growth, and constrained variables | Represents additive processes, symmetric shocks, and unconstrained variables |
| Examples | Income distribution, stock prices, inflation rates | Error terms in regression, human heights, interest rates fluctuations |
Introduction to Log-Normal and Normal Distributions
Log-normal distribution models data whose logarithm is normally distributed, often applied in finance, biology, and environmental sciences to represent positive-valued, skewed data. Normal distribution, characterized by its symmetric bell-shaped curve, describes many natural phenomena with data centered around a mean and evenly distributed variability. Understanding the distinctions in shape, scale, and underlying processes between log-normal and normal distributions is crucial for accurate statistical modeling and data interpretation.
Defining the Normal Distribution
The Normal distribution, also known as the Gaussian distribution, is defined by its symmetric, bell-shaped curve characterized by the mean (m) and standard deviation (s), representing the central tendency and dispersion of data respectively. Unlike the Log-normal distribution, which models variables whose logarithms are normally distributed and is skewed right, the Normal distribution assumes data can take any real value, including negatives. This fundamental difference makes the Normal distribution ideal for representing naturally occurring phenomena with symmetric variability around the mean.
Understanding the Log-Normal Distribution
The log-normal distribution describes a random variable whose logarithm is normally distributed, meaning data is positively skewed and bounded by zero, unlike the symmetric normal distribution that extends infinitely in both directions. This distribution effectively models phenomena such as stock prices, income levels, and biological measurements, where values cannot be negative and multiplicative processes dominate. Parameters like the mean and standard deviation of the underlying normal distribution's logarithm determine the shape and scale of the log-normal distribution, making it essential for accurate risk assessment and probabilistic forecasting in finance and engineering.
Mathematical Formulations and Properties
The normal distribution is characterized by its symmetric bell-shaped curve defined by the probability density function \( f(x) = \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{(x-\mu)^2}{2\sigma^2}} \), where \(\mu\) is the mean and \(\sigma\) is the standard deviation. The log-normal distribution, defined as the distribution of a variable whose logarithm is normally distributed, has the probability density function \( f(x) = \frac{1}{x\sigma\sqrt{2\pi}} e^{-\frac{(\ln x - \mu)^2}{2\sigma^2}} \) for \(x > 0\), making it positively skewed and bounded below by zero. Unlike the normal distribution, the log-normal distribution models multiplicative processes, exhibits skewness and a heavier tail, and its moments are functions of both \(\mu\) and \(\sigma\), with mean \(e^{\mu + \sigma^2/2}\) and variance \((e^{\sigma^2} - 1)e^{2\mu + \sigma^2}\).
Key Differences Between Log-Normal and Normal Distributions
The log-normal distribution models variables whose logarithms follow a normal distribution, resulting in a skewed, positively bounded distribution, unlike the symmetric, unbounded normal distribution that can take any real value. Key differences include the log-normal's non-negative support and right skewness versus the normal's symmetric bell curve around its mean. Applications vary: log-normal distributions often model stock prices, rainfall, and income, while normal distributions suit measurement errors and natural phenomena with symmetric variability.
Real-World Applications of Normal Distribution
The Normal distribution plays a crucial role in fields like finance, natural sciences, and social sciences due to its properties that model random variables symmetrically around the mean, making it ideal for representing measurement errors and natural phenomena such as heights, test scores, and IQ distributions. In contrast, the Log-normal distribution is often used for modeling non-negative data skewed to the right, such as stock prices, income distribution, and environmental data, where values cannot fall below zero and tend to grow multiplicatively. Practical applications of the Normal distribution include risk assessment in portfolio management, quality control in manufacturing, and hypothesis testing in statistics, leveraging its well-understood parameters of mean and variance.
Practical Uses of Log-Normal Distribution
Log-normal distribution is favored in modeling financial asset prices, where values cannot be negative and exhibit multiplicative growth, unlike the symmetric normal distribution. It accurately represents real-world phenomena such as stock prices, income distribution, and product life spans, which often skew positively. Practical applications include risk assessment, option pricing, and environmental data analysis where growth rates and volatility are naturally log-normally distributed.
Data Visualization and Interpretation
Log-normal distribution data appear skewed right on standard linear scales, making it essential to use logarithmic transformations for accurate visualization and interpretation, unlike the symmetric bell curve seen in normal distribution. Visualizing log-normal data on a log scale linearizes the distribution, highlighting multiplicative effects and enabling clearer insights into data spread and central tendency. Normal distribution data maintain consistent mean and variance properties, facilitating straightforward interpretation with common statistical tools such as histograms and Q-Q plots.
Choosing the Right Distribution for Your Data
Selecting the appropriate distribution hinges on the nature of your data: Normal distribution suits symmetric data with constant variance, centered around a mean. Log-normal distribution applies when data are positively skewed, non-negative, and multiplicative processes drive variability. Analyzing skewness, variance stability, and data range helps determine whether Normal or Log-normal distribution better models your dataset.
Summary and Conclusion
The log-normal distribution models data that are positively skewed and multiplicatively determined, often representing variables that cannot be negative, such as stock prices or biological measurements. In contrast, the normal distribution assumes symmetry and additive effects, fitting many natural phenomena like heights and test scores. Choosing between these distributions depends on the data's properties: log-normal is suited for right-skewed, non-negative data, while normal distribution fits symmetric, unbounded variables.
Log-normal distribution Infographic
 libterm.com
libterm.com