The consumption-based model charges customers only for the resources or services they actually use, promoting cost efficiency and flexibility. This approach eliminates upfront investments and aligns expenses with actual demand, ideal for businesses seeking scalable solutions. Discover how this model can optimize Your spending and operational strategy in the full article.
Table of Comparison
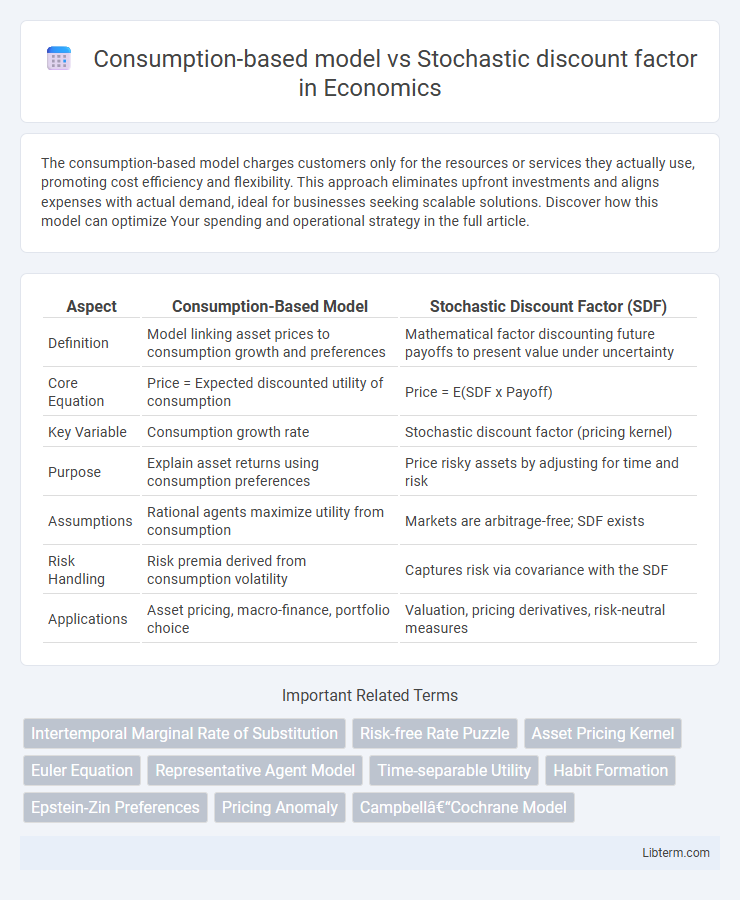
| Aspect | Consumption-Based Model | Stochastic Discount Factor (SDF) |
|---|---|---|
| Definition | Model linking asset prices to consumption growth and preferences | Mathematical factor discounting future payoffs to present value under uncertainty |
| Core Equation | Price = Expected discounted utility of consumption | Price = E(SDF x Payoff) |
| Key Variable | Consumption growth rate | Stochastic discount factor (pricing kernel) |
| Purpose | Explain asset returns using consumption preferences | Price risky assets by adjusting for time and risk |
| Assumptions | Rational agents maximize utility from consumption | Markets are arbitrage-free; SDF exists |
| Risk Handling | Risk premia derived from consumption volatility | Captures risk via covariance with the SDF |
| Applications | Asset pricing, macro-finance, portfolio choice | Valuation, pricing derivatives, risk-neutral measures |
Introduction to Asset Pricing Models
Consumption-based models in asset pricing link investors' consumption patterns directly to asset returns by explaining how consumption risk influences expected returns, emphasizing the representative agent's intertemporal optimization behavior. The stochastic discount factor (SDF) framework generalizes this approach by assigning state-price densities that price all assets consistently, capturing risk preferences and time value through a single pricing kernel. These models jointly form the foundation of modern asset pricing theory, enabling evaluation of equilibrium prices in incomplete markets and under uncertainty.
Understanding the Consumption-Based Model
The Consumption-Based Model (CBM) explains asset prices through the intertemporal consumption choices of investors, linking expected returns to marginal utility derived from consumption growth. This model emphasizes how risk aversion and consumption volatility shape the stochastic discount factor, which adjusts future payoffs to present value based on consumers' preferences. Understanding CBM requires analyzing how consumption patterns influence discount rates and consequently impact asset pricing in financial markets.
Key Concepts in the Stochastic Discount Factor
The stochastic discount factor (SDF) is a fundamental concept in asset pricing representing the present value of future payoffs by incorporating risk preferences and time value of money. It links consumption-based models to market data by capturing how agents value uncertain future consumption streams through marginal utility growth. Key features include pricing kernel properties, the martingale condition ensuring no arbitrage, and the SDF's covariance with asset returns determining risk premia in equilibrium.
Historical Evolution of Asset Pricing Approaches
The historical evolution of asset pricing approaches reveals a transition from consumption-based models, which estimate asset values through utility maximization and intertemporal consumption choices, to stochastic discount factor (SDF) frameworks that incorporate probabilistic discounting based on state prices. Early consumption-based models, such as the Consumption Capital Asset Pricing Model (CCAPM), faced empirical challenges due to difficulty in measuring consumption risk premiums. The development of SDF approaches enabled more flexible, model-independent asset pricing by linking expected payoffs directly to stochastic discount factors inferred from financial market data.
Core Differences: Consumption-Based vs Stochastic Discount Factor
The consumption-based model estimates asset prices by linking them directly to intertemporal consumption choices, emphasizing the marginal utility of consumption over time. In contrast, the stochastic discount factor (SDF) is a more general pricing kernel that adjusts payoffs by accounting for investors' risk preferences and states of the world without relying solely on consumption data. Core differences lie in the consumption-based model's explicit foundation on consumption growth dynamics, while the SDF framework provides a flexible, often state-dependent measure that can incorporate various risk factors beyond consumption.
Theoretical Foundations and Mathematical Frameworks
The consumption-based model relies on the intertemporal optimization framework where agent preferences are represented by utility functions defined over consumption streams, and asset prices derive from the marginal rate of substitution in consumption. The stochastic discount factor (SDF) embeds this intertemporal marginal rate of substitution as a random variable discounting future payoffs, serving as a unifying tool in asset pricing theory that connects risk preferences, consumption growth, and return dynamics. Mathematically, the consumption-based model formulates the SDF as \( M_{t+1} = \beta \frac{u'(C_{t+1})}{u'(C_t)} \), where \( \beta \) is the subjective discount factor and \( u'(\cdot) \) is the marginal utility of consumption, establishing a direct link between consumption dynamics and pricing kernels.
Practical Applications and Implications
The consumption-based model directly links asset prices to individual consumption patterns, facilitating portfolio optimization and risk assessment in personal finance and macroeconomic policy design. In contrast, the stochastic discount factor (SDF) provides a more flexible framework by capturing the pricing kernel across uncertain future states, enabling advanced derivative pricing and risk-neutral valuation in financial markets. Practical applications of the consumption-based model include forecasting equity premiums, while the SDF is critical for calibrating models in dynamic asset allocation and pricing complex securities.
Strengths and Limitations of Each Model
The consumption-based model provides a direct link between consumption patterns and asset prices, effectively capturing the impact of intertemporal choices and risk aversion but often struggles with empirical inconsistencies and difficulty in explaining observed asset return anomalies. The stochastic discount factor (SDF) framework offers greater flexibility by incorporating a range of state variables and better fits complex financial data, yet it may lack intuitive economic interpretation and relies heavily on the accurate specification of underlying dynamics. Both models serve crucial roles in asset pricing, where the consumption-based approach excels in theoretical clarity, while the SDF approach enhances empirical robustness and adaptability.
Empirical Evidence and Real-World Performance
Empirical evidence shows that consumption-based models often struggle to fully explain asset prices and risk premiums observed in real markets, as these models rely heavily on accurate consumption data and representative agents. In contrast, stochastic discount factor (SDF) approaches, particularly those calibrated with market returns and state variables, tend to offer superior real-world performance by capturing dynamic risk adjustments more effectively. Studies comparing both frameworks highlight that SDF models produce more consistent pricing kernels and better align with observed asset return distributions, especially during periods of economic volatility.
Future Directions in Asset Pricing Research
Future directions in asset pricing research highlight the integration of consumption-based models with stochastic discount factors to improve empirical accuracy and theoretical robustness. Advancements in machine learning and high-frequency data analysis enable more precise estimation of dynamic risk factors influencing asset prices over time. Emphasizing heterogeneous agent models and behavioral finance can refine stochastic discount factor formulations, addressing observed market anomalies and enhancing predictive power.
Consumption-based model Infographic
 libterm.com
libterm.com