Nonlinear oscillation occurs when the restoring force in a system is not directly proportional to displacement, leading to complex behaviors like amplitude-dependent frequencies and chaotic motion. Understanding these oscillations is crucial for predicting the dynamics in mechanical, electrical, and biological systems. Explore the rest of the article to deepen your insight into nonlinear oscillation and its real-world applications.
Table of Comparison
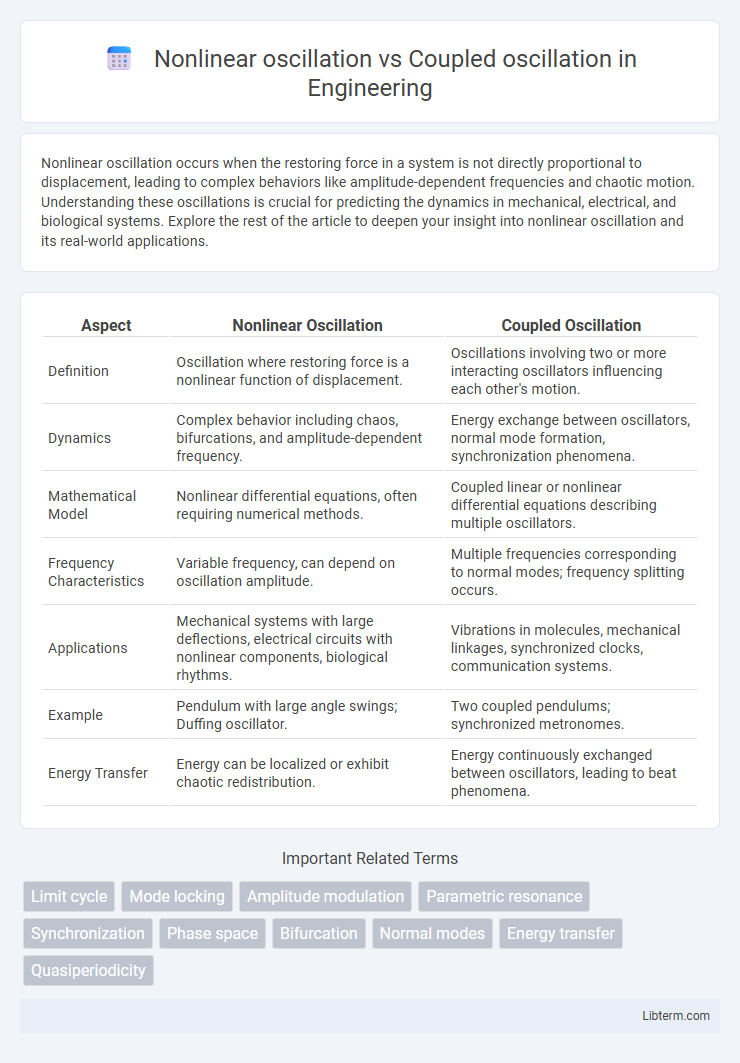
| Aspect | Nonlinear Oscillation | Coupled Oscillation |
|---|---|---|
| Definition | Oscillation where restoring force is a nonlinear function of displacement. | Oscillations involving two or more interacting oscillators influencing each other's motion. |
| Dynamics | Complex behavior including chaos, bifurcations, and amplitude-dependent frequency. | Energy exchange between oscillators, normal mode formation, synchronization phenomena. |
| Mathematical Model | Nonlinear differential equations, often requiring numerical methods. | Coupled linear or nonlinear differential equations describing multiple oscillators. |
| Frequency Characteristics | Variable frequency, can depend on oscillation amplitude. | Multiple frequencies corresponding to normal modes; frequency splitting occurs. |
| Applications | Mechanical systems with large deflections, electrical circuits with nonlinear components, biological rhythms. | Vibrations in molecules, mechanical linkages, synchronized clocks, communication systems. |
| Example | Pendulum with large angle swings; Duffing oscillator. | Two coupled pendulums; synchronized metronomes. |
| Energy Transfer | Energy can be localized or exhibit chaotic redistribution. | Energy continuously exchanged between oscillators, leading to beat phenomena. |
Introduction to Oscillatory Systems
Nonlinear oscillation involves systems where restoring forces are not proportional to displacement, leading to complex behaviors such as amplitude-dependent frequencies and chaotic motion. Coupled oscillation occurs when two or more oscillators interact through a coupling mechanism, resulting in energy exchange and phenomena like mode splitting and synchronization. Understanding these fundamental differences is crucial for analyzing diverse oscillatory systems in physics, engineering, and biology.
Defining Nonlinear Oscillation
Nonlinear oscillation occurs when the restoring force is not proportional to displacement, resulting in complex dynamic behavior such as amplitude-dependent frequencies and bifurcations. Unlike coupled oscillations, which involve interactions between two or more oscillators influencing each other's motion, nonlinear oscillations are characterized by intrinsic system properties leading to phenomena like chaos and limit cycles. Understanding nonlinear oscillations is essential for analyzing real-world systems in physics, engineering, and biology where linear assumptions fail.
Exploring Coupled Oscillation
Coupled oscillation involves two or more oscillators linked so that energy transfers between them, producing complex motion patterns and synchronization effects not seen in individual nonlinear oscillations. Exploring coupled oscillations reveals phenomena such as mode splitting, frequency entrainment, and amplitude modulation that emerge from the interaction of oscillators with nonlinear dynamics. Understanding these interactions is crucial for applications in mechanical systems, biological rhythms, and electrical circuits where energy exchange and stability are critical.
Key Differences: Nonlinear vs Coupled Oscillations
Nonlinear oscillations occur when the restoring force depends nonlinearly on displacement, leading to complex behaviors like amplitude-dependent frequencies and potential chaotic dynamics. Coupled oscillations involve two or more interacting oscillators exchanging energy, resulting in synchronized or mode-splitting phenomena influenced by the strength of coupling. The key difference lies in nonlinearity affecting individual oscillator dynamics, whereas coupling focuses on interactions between oscillators altering collective motion.
Mathematical Modeling of Nonlinear Oscillators
Mathematical modeling of nonlinear oscillators involves differential equations with nonlinear terms that capture phenomena such as limit cycles, bifurcations, and chaos, distinguishing them from linear coupled oscillations governed by linear superposition principles. Nonlinear oscillators require techniques like phase plane analysis, perturbation methods, and numerical simulations to analyze stability and periodic behavior in systems ranging from mechanical pendulums to biological rhythms. Coupled oscillations often use systems of linear differential equations to describe energy or information exchange, whereas nonlinear models account for complex interactions and amplitude-dependent frequencies inherent in real-world applications.
Mathematical Representation of Coupled Oscillators
Coupled oscillators are mathematically represented using systems of differential equations that describe the interaction between two or more oscillatory components, often involving matrices or coupled second-order linear differential equations. Unlike nonlinear oscillations, where individual oscillators exhibit nonlinear dynamics typically governed by nonlinear differential equations, coupled oscillations emphasize the linear or nonlinear coupling terms that affect the phase and amplitude relationships between oscillators. The mathematical framework utilizes eigenvalue analysis and normal modes to characterize the collective behavior and resonance phenomena arising from the coupling.
Real-World Examples of Nonlinear Oscillation
Nonlinear oscillation occurs in real-world systems such as the swinging motion of a pendulum with large amplitude, the heartbeat regulated by the sinoatrial node, and the chaotic vibrations in mechanical structures like bridges during earthquakes. Coupled oscillation involves interacting oscillators, commonly seen in synchronized fireflies or coupled pendulums. Nonlinear oscillations exhibit complex behaviors like amplitude-dependent frequencies and bifurcations, distinguishing them from the predictable patterns of coupled oscillations.
Real-World Applications of Coupled Oscillation
Coupled oscillation plays a critical role in real-world applications such as synchronization in power grids, where multiple generators must operate in concert to maintain stable electricity supply. Biomechanical systems, including heart cells, utilize coupled oscillations to achieve coordinated contractions necessary for effective blood circulation. In communication technologies, coupled oscillators enable signal processing and frequency control, enhancing the performance of wireless networks and electronic devices.
Challenges in Analyzing Nonlinear and Coupled Systems
Analyzing nonlinear oscillations presents challenges due to their sensitivity to initial conditions, potential for chaotic behavior, and lack of closed-form solutions, complicating prediction and control. Coupled oscillations introduce complexities such as mode interactions, synchronization phenomena, and energy transfer between oscillators, which require advanced mathematical techniques like perturbation methods or numerical simulations. Both systems demand significant computational resources and sophisticated analytical frameworks to address instability, bifurcations, and multiscale dynamics effectively.
Future Research in Oscillatory Dynamics
Future research in oscillatory dynamics will increasingly explore the intersection of nonlinear oscillation and coupled oscillation to better understand complex systems such as neural networks and climate models. Advances in mathematical modeling and computational methods are expected to enhance prediction accuracy and control strategies for chaotic behaviors in coupled nonlinear oscillators. Integrating machine learning techniques with experimental data promises to uncover new insights into synchronization phenomena and energy transfer mechanisms in multi-oscillator systems.
Nonlinear oscillation Infographic
 libterm.com
libterm.com