Blasius analogy is a fundamental concept in fluid dynamics that relates heat transfer to momentum transfer in laminar boundary layers. It establishes a connection between the velocity profile and temperature distribution, enabling engineers to predict heat transfer rates based on flow characteristics. Explore the rest of this article to understand how Blasius analogy can optimize your thermal management strategies.
Table of Comparison
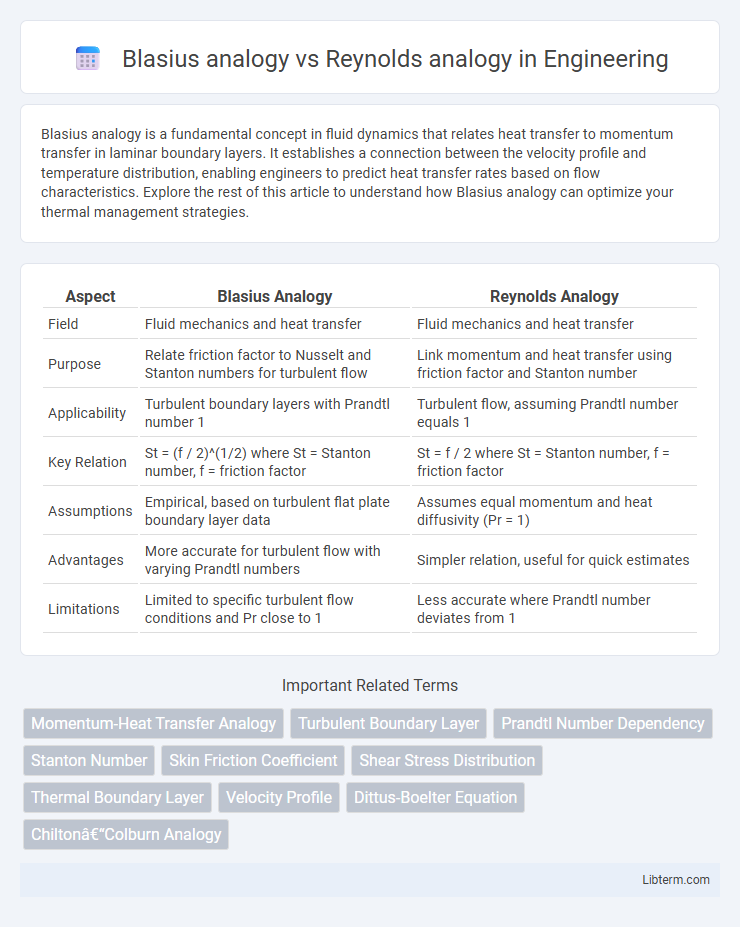
| Aspect | Blasius Analogy | Reynolds Analogy |
|---|---|---|
| Field | Fluid mechanics and heat transfer | Fluid mechanics and heat transfer |
| Purpose | Relate friction factor to Nusselt and Stanton numbers for turbulent flow | Link momentum and heat transfer using friction factor and Stanton number |
| Applicability | Turbulent boundary layers with Prandtl number 1 | Turbulent flow, assuming Prandtl number equals 1 |
| Key Relation | St = (f / 2)^(1/2) where St = Stanton number, f = friction factor | St = f / 2 where St = Stanton number, f = friction factor |
| Assumptions | Empirical, based on turbulent flat plate boundary layer data | Assumes equal momentum and heat diffusivity (Pr = 1) |
| Advantages | More accurate for turbulent flow with varying Prandtl numbers | Simpler relation, useful for quick estimates |
| Limitations | Limited to specific turbulent flow conditions and Pr close to 1 | Less accurate where Prandtl number deviates from 1 |
Introduction to Heat and Momentum Transfer Analogies
Blasius analogy relates the velocity profile in laminar boundary layers to heat transfer by linking the momentum and thermal boundary layers through a similarity solution, primarily valid for laminar flow regimes. Reynolds analogy establishes a direct proportionality between momentum and heat transfer coefficients based on turbulent flow characteristics, assuming equal diffusivities of momentum and heat. Both analogies serve as foundational concepts in analyzing convective heat transfer by connecting fluid flow behavior to thermal transport phenomena.
Overview of Blasius Analogy
Blasius analogy relates laminar boundary layer momentum and heat transfer, providing a correlation between the velocity and temperature profiles using the Prandtl number as a key parameter. It is commonly applied in fluid dynamics to predict heat transfer rates in laminar flows over flat plates. This analogy is particularly useful for fluids with Prandtl numbers close to unity, offering improved accuracy over Reynolds analogy in such conditions.
Fundamentals of Reynolds Analogy
Reynolds analogy establishes a fundamental relationship between momentum and heat transfer in turbulent flows by equating the Stanton number to half the friction factor, highlighting the direct proportionality of convective heat transfer and fluid friction. It assumes similar velocity and thermal boundary layers, allowing prediction of heat transfer coefficients from measured friction factors. This simplification is essential for analyzing turbulent flow heat transfer where detailed velocity and temperature profiles are complex to obtain.
Mathematical Formulation: Blasius vs Reynolds
The Blasius analogy is mathematically formulated using the similarity solutions of the boundary layer equations, linking the dimensionless velocity gradient to heat transfer via the Prandtl number and friction coefficient, typically expressed as \( St = \frac{C_f}{2} \cdot Pr^{1/3} \). In contrast, the Reynolds analogy establishes a direct proportionality between the Stanton number \( St \) and half the skin friction coefficient \( C_f/2 \) under the assumption of unity Prandtl number and turbulent flow, summarized as \( St = \frac{C_f}{2} \). The Blasius formulation applies primarily to laminar flow with constant properties, while Reynolds analogy is more suited for turbulent flow regimes with simplified assumptions in heat and momentum transfer correlations.
Assumptions and Limitations of Each Analogy
Blasius analogy assumes laminar flow over a flat plate and applies strictly to smooth surfaces with a constant fluid property, limiting its accuracy for turbulent or rough wall conditions. Reynolds analogy presumes equal turbulent Prandtl and Schmidt numbers, linking momentum and heat transfer but neglects variations in molecular diffusivities and temperature-dependent fluid properties. Both analogies face limitations in complex flows, such as those with significant pressure gradients, heat generation, or compressibility effects, which reduce their predictive reliability.
Applicability in Laminar and Turbulent Flows
Blasius analogy applies primarily to laminar boundary layer flows, relating the velocity and thermal boundary layers by assuming similarity between momentum and heat transfer in these smooth, orderly flows. Reynolds analogy extends applicability to turbulent flows by linking momentum and heat transfer through empirical correlations, accounting for the complex eddy diffusivity in turbulent boundary layers. While Blasius analogy provides accurate predictions for laminar flows, Reynolds analogy is more suitable for turbulent flow conditions where mixing enhances heat and momentum transfer.
Key Differences between Blasius and Reynolds Analogies
Blasius and Reynolds analogies both relate momentum and heat transfer in fluid flow but differ significantly in their applications and assumptions. Blasius analogy specifically applies to laminar flow over flat plates with constant properties, focusing on velocity profile similarity, while Reynolds analogy extends to turbulent flow, assuming unity Prandtl number and parallel momentum and heat transfer mechanisms. The key difference lies in Blasius analogy's empirical derivation for laminar conditions and Reynolds analogy's theoretical basis for turbulent flows with simplified thermal and velocity boundary layer interactions.
Practical Engineering Applications
Blasius analogy primarily aids in predicting turbulent flow friction factors in smooth pipe flows, offering practical utility in hydraulic and pipeline engineering by simplifying friction loss calculations. Reynolds analogy connects heat transfer and momentum transfer coefficients, enabling engineers to estimate convective heat transfer from known friction factors, which is invaluable in thermal system design such as heat exchangers and cooling channels. Both analogies provide critical insights for optimizing fluid flow and heat transfer performance in industrial applications, with Blasius serving mainly fluid mechanics and Reynolds facilitating thermo-fluid analysis.
Experimental Validation and Accuracy
Blasius analogy demonstrates higher experimental validation in laminar boundary layer flows due to its basis on empirical correlations, making it accurate for low Reynolds number conditions. Reynolds analogy extends applicability to turbulent flows by linking heat and momentum transfer but often shows deviations in experimental accuracy because it assumes equal turbulent Prandtl and Schmidt numbers. Experimental data consistently reveal that Blasius analogy provides precise predictions for smooth, low-speed flows, whereas Reynolds analogy requires correction factors for high turbulence and complex geometries to improve accuracy.
Summary and Comparative Insights
Blasius analogy relates skin friction to heat transfer for laminar boundary layers, emphasizing velocity and temperature profiles without requiring turbulent flow assumptions. Reynolds analogy extends this concept to turbulent flows, linking momentum and heat transfer through the Reynolds number and Prandtl number, often used for engineering heat exchanger design. Comparing both, Blasius provides precise predictions in laminar regimes, while Reynolds analogy offers practical estimates in turbulent conditions, though it may oversimplify complex heat and momentum transfer interactions.
Blasius analogy Infographic
 libterm.com
libterm.com