Natural frequency refers to the specific rate at which a system oscillates when disturbed from its equilibrium position without external forces. Understanding natural frequency is crucial for designing structures and machines to avoid resonance, which can lead to failure or damage. Explore the rest of the article to learn how natural frequency impacts your engineering projects and everyday applications.
Table of Comparison
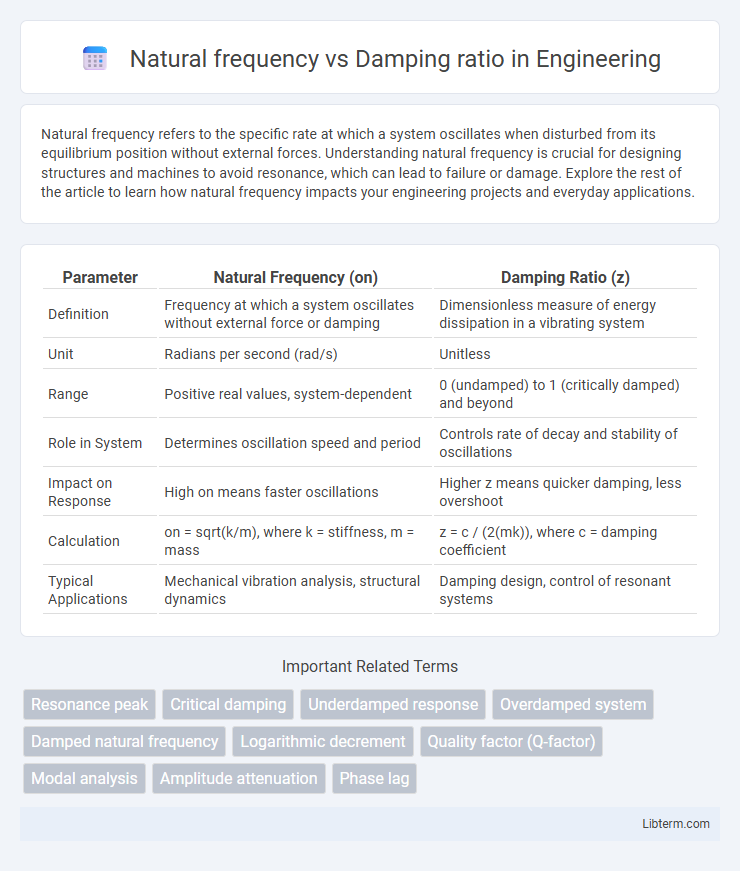
| Parameter | Natural Frequency (on) | Damping Ratio (z) |
|---|---|---|
| Definition | Frequency at which a system oscillates without external force or damping | Dimensionless measure of energy dissipation in a vibrating system |
| Unit | Radians per second (rad/s) | Unitless |
| Range | Positive real values, system-dependent | 0 (undamped) to 1 (critically damped) and beyond |
| Role in System | Determines oscillation speed and period | Controls rate of decay and stability of oscillations |
| Impact on Response | High on means faster oscillations | Higher z means quicker damping, less overshoot |
| Calculation | on = sqrt(k/m), where k = stiffness, m = mass | z = c / (2(mk)), where c = damping coefficient |
| Typical Applications | Mechanical vibration analysis, structural dynamics | Damping design, control of resonant systems |
Introduction to Natural Frequency and Damping Ratio
Natural frequency refers to the inherent oscillation rate of a system when disturbed from its equilibrium position without external forces or damping effects. Damping ratio quantifies the degree of energy dissipation in a vibrating system, influencing how oscillations decay over time. Understanding the relationship between natural frequency and damping ratio is essential for predicting system stability and behavior in mechanical and structural engineering applications.
Defining Natural Frequency
Natural frequency refers to the inherent rate at which a system oscillates when disturbed from its equilibrium position without any external forces or damping effects. It is a fundamental property of mechanical and structural systems, depending on mass and stiffness. Understanding natural frequency is crucial for analyzing vibration behavior and avoiding resonance, which can lead to excessive amplitude and potential failure.
Understanding Damping Ratio
Damping ratio quantifies the extent of energy dissipation in an oscillatory system relative to its natural frequency, directly affecting how quickly vibrations diminish. A higher damping ratio results in faster decay of oscillations and prevents sustained or excessive resonance, enhancing system stability. Understanding the damping ratio is crucial for designing structures and mechanical systems to control vibrations and avoid damage caused by resonance phenomena.
Mathematical Relationship between Natural Frequency and Damping Ratio
The mathematical relationship between natural frequency (o_n) and damping ratio (z) is expressed by the damped natural frequency (o_d), calculated as o_d = o_n(1 - z2). This formula shows how damping ratio reduces the system's oscillation frequency from its undamped natural frequency o_n. When z approaches zero, o_d approximates o_n, indicating minimal damping effect on oscillations.
Importance in Mechanical and Structural Systems
Natural frequency determines the rate at which a mechanical or structural system oscillates when displaced from its equilibrium position, directly influencing its dynamic response to external forces. The damping ratio quantifies the system's ability to dissipate energy and reduce oscillations, critical for preventing excessive vibrations and potential structural failure. Optimizing both natural frequency and damping ratio ensures stability, longevity, and safety in engineering applications such as bridges, buildings, and machinery.
How Damping Affects System Response
Damping ratio directly influences the amplitude and decay rate of oscillations in a system's natural frequency response, determining whether vibrations persist or diminish quickly. Higher damping ratios reduce overshoot and speed up the settling time, leading to more stable and controlled system behavior. Systems with low damping ratios exhibit prolonged oscillations and sustained vibrations near their natural frequency, increasing the risk of resonance-related damage.
Types of Damping: Under, Critical, and Overdamped
Natural frequency defines the rate at which a system oscillates without external forces, while the damping ratio quantifies energy loss during these oscillations. Types of damping include underdamped systems, where oscillations gradually reduce amplitude and damping ratio is less than one; critically damped systems, with a damping ratio equal to one, eliminating oscillations and returning to equilibrium swiftly; and overdamped systems, where the damping ratio exceeds one, causing a slow return to equilibrium without oscillations. Each damping type distinctly influences system stability and response time in mechanical and electrical applications.
Practical Examples in Engineering Applications
Natural frequency and damping ratio critically influence the performance of engineering systems such as automotive suspension and building structures during earthquakes. Automotive suspension systems are designed with specific natural frequencies to absorb road shocks effectively, while appropriate damping ratios prevent excessive oscillations, enhancing ride comfort and safety. In earthquake engineering, structures are tuned with optimized natural frequencies to avoid resonance with seismic waves, and adequate damping ratios dissipate energy, reducing potential structural damage.
Measuring and Calculating Natural Frequency and Damping Ratio
Natural frequency is measured using frequency response functions obtained from experimental modal analysis, where sensors capture the system's vibration response to a known excitation. Damping ratio is calculated by analyzing the decay rate of free vibrations or extracting logarithmic decrement from time-domain response data, providing insight into energy dissipation. Both parameters are essential in dynamic system characterization and are derived through signal processing techniques such as Fast Fourier Transform (FFT) and curve fitting to resonance peaks.
Conclusion: Optimizing System Performance
Optimizing system performance requires a precise balance between natural frequency and damping ratio to achieve desired responsiveness and stability. A higher natural frequency enhances system speed, while an optimal damping ratio minimizes overshoot and oscillations, ensuring smooth operation. Tuning these parameters based on specific application requirements leads to improved efficiency, reduced wear, and enhanced reliability in dynamic systems.
Natural frequency Infographic
 libterm.com
libterm.com