The control volume approach simplifies complex fluid flow and heat transfer problems by focusing on a defined region in space to analyze the mass, momentum, and energy entering and leaving that region. This method is essential in engineering fields like thermodynamics and fluid mechanics, enabling precise calculations of system behavior without tracking every particle. Explore the rest of the article to enhance your understanding of how the control volume approach can be applied to solve practical engineering challenges.
Table of Comparison
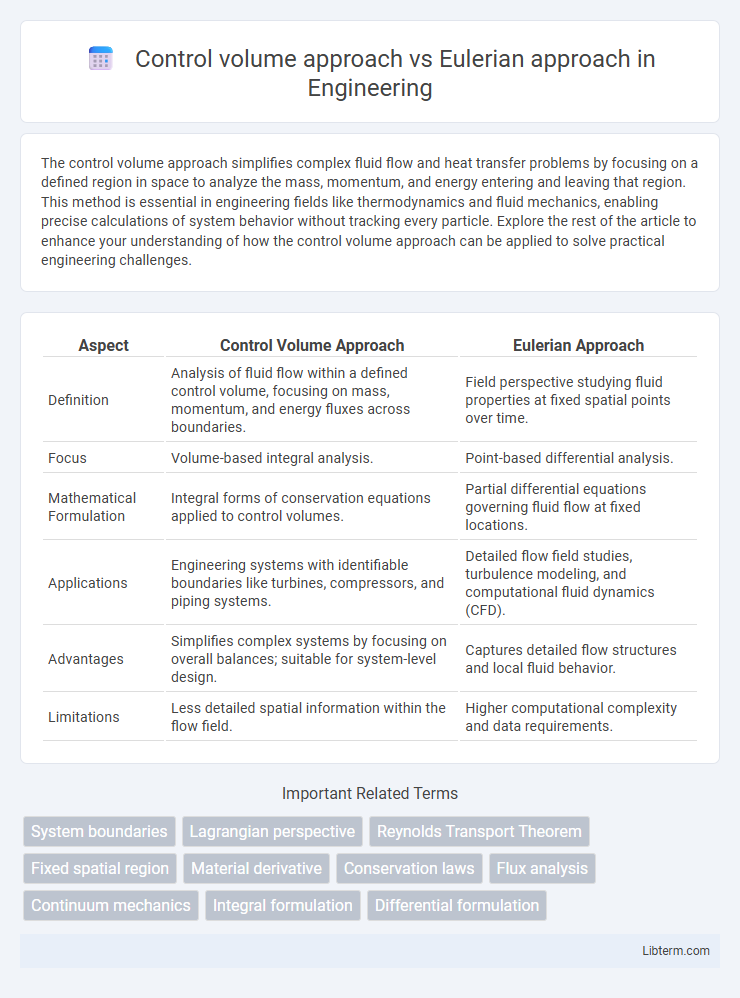
| Aspect | Control Volume Approach | Eulerian Approach |
|---|---|---|
| Definition | Analysis of fluid flow within a defined control volume, focusing on mass, momentum, and energy fluxes across boundaries. | Field perspective studying fluid properties at fixed spatial points over time. |
| Focus | Volume-based integral analysis. | Point-based differential analysis. |
| Mathematical Formulation | Integral forms of conservation equations applied to control volumes. | Partial differential equations governing fluid flow at fixed locations. |
| Applications | Engineering systems with identifiable boundaries like turbines, compressors, and piping systems. | Detailed flow field studies, turbulence modeling, and computational fluid dynamics (CFD). |
| Advantages | Simplifies complex systems by focusing on overall balances; suitable for system-level design. | Captures detailed flow structures and local fluid behavior. |
| Limitations | Less detailed spatial information within the flow field. | Higher computational complexity and data requirements. |
Introduction to Control Volume and Eulerian Approaches
Control volume approach analyzes fluid flow by defining a fixed region in space through which fluid passes, facilitating the application of conservation laws for mass, momentum, and energy within that volume. The Eulerian approach focuses on specific spatial locations and examines how fluid properties such as velocity, pressure, and density change over time at these fixed points. Both methods provide complementary perspectives in fluid dynamics, enabling detailed understanding and quantification of flow behavior using differential and integral formulations.
Fundamental Concepts: Control Volume Explained
The Control Volume approach analyzes fluid flow by examining a fixed region in space through which fluid passes, focusing on the net flux of mass, momentum, and energy across its boundaries. This method utilizes the Reynolds Transport Theorem to relate system properties to control volume properties, facilitating the application of conservation laws in a practical and manageable form. Unlike the Eulerian approach, which studies fluid properties at specific points over time, the Control Volume approach emphasizes the overall behavior within the spatial boundary, making it essential for engineering system analyses.
Understanding the Eulerian Approach
The Eulerian approach analyzes fluid flow by examining changes in velocity, pressure, and other properties at fixed points in space over time, rather than tracking individual fluid particles. This method utilizes a control volume framework where the flow variables are functions of spatial coordinates and time, allowing for the application of conservation laws such as mass, momentum, and energy within a defined region. The Eulerian approach is fundamental in computational fluid dynamics (CFD) for solving complex flow problems involving turbulence, compressibility, and unsteady conditions.
Mathematical Formulation of Control Volume Method
The mathematical formulation of the Control Volume Method involves applying the integral form of conservation laws--mass, momentum, and energy--over a finite control volume, translating physical phenomena into algebraic equations. This approach discretizes the domain into control volumes where fluxes across boundaries are computed, enabling accurate representation of flow quantities and their changes within each volume. Unlike the Eulerian approach, which uses point-wise differential equations, the Control Volume Method emphasizes integral balances, enhancing numerical stability and conservation accuracy in fluid dynamics simulations.
Mathematical Structure of Eulerian Analysis
Eulerian analysis employs a fixed control volume through which fluid properties such as velocity, pressure, and density are observed as functions of space and time, facilitating the use of partial differential equations like the Navier-Stokes equations. The mathematical structure focuses on solving these equations within a control volume using spatial and temporal derivatives to capture the fluid flow behavior at specific locations. This approach contrasts with the control volume method that integrates fluxes over boundaries, emphasizing localized field variables and differential form representation in Eulerian analysis.
Key Differences: Control Volume vs Eulerian Approach
The control volume approach focuses on analyzing fluid flow by examining a fixed region in space through which fluid passes, allowing conservation laws to be applied to mass, momentum, and energy entering and leaving the volume. The Eulerian approach also observes fluid properties at specific fixed points in space over time but emphasizes the local velocity and flow field variables without explicitly defining a bounded region. Key differences include the control volume's emphasis on boundary fluxes and integral conservation equations, while the Eulerian framework primarily deals with differential equations defining flow behavior at points within the fluid domain.
Advantages of the Control Volume Method
The Control Volume Method excels in analyzing fluid flow by simplifying complex systems into manageable regions, enabling straightforward application of conservation laws for mass, momentum, and energy. This approach enhances computational efficiency and accuracy by focusing on fluxes across control surfaces rather than detailed pointwise flow properties. It offers greater flexibility in handling varying geometries and boundary conditions compared to the Eulerian approach, making it ideal for engineering applications such as CFD simulations and heat exchanger design.
Benefits of the Eulerian Approach
The Eulerian approach excels in analyzing fluid flow by focusing on specific locations in space, allowing for continuous monitoring of velocity, pressure, and other properties at fixed points. This method simplifies the mathematical modeling of complex, time-dependent flows and is highly beneficial in computational fluid dynamics (CFD) simulations. Its ability to handle large-scale systems with varying boundary conditions provides significant advantages over the control volume approach in both accuracy and efficiency.
Applications and Suitability in Engineering Fields
The control volume approach excels in fluid mechanics and thermodynamics by enabling precise analysis of mass, momentum, and energy exchanges within a defined boundary, making it ideal for engineering applications like heat exchangers, turbines, and combustion engines. The Eulerian approach, focusing on specific points in space with fixed coordinates, is highly suitable for computational fluid dynamics (CFD) simulations, aerodynamic studies, and environmental engineering where fluid flow patterns and temporal changes are critical. Engineers select the control volume method for system-level conservation analysis and the Eulerian method for detailed flowfield visualization and transient flow behavior assessment.
Conclusion: Choosing the Right Approach for Your Problem
Selecting the appropriate method between the control volume approach and the Eulerian approach depends on the specific characteristics and requirements of the fluid flow problem. The control volume approach excels in analyzing conservation laws over finite regions, making it suitable for engineering applications involving complex boundary interactions. The Eulerian approach is ideal for detailed flow field descriptions at fixed spatial locations, often preferred in computational fluid dynamics simulations for capturing transient and spatial variations effectively.
Control volume approach Infographic
 libterm.com
libterm.com