Elastic contact occurs when two deformable bodies come into contact and experience reversible deformation without permanent damage. This phenomenon is critical in understanding stress distribution, friction, and wear in mechanical systems. Explore the rest of the article to learn how elastic contact principles impact engineering design and material selection.
Table of Comparison
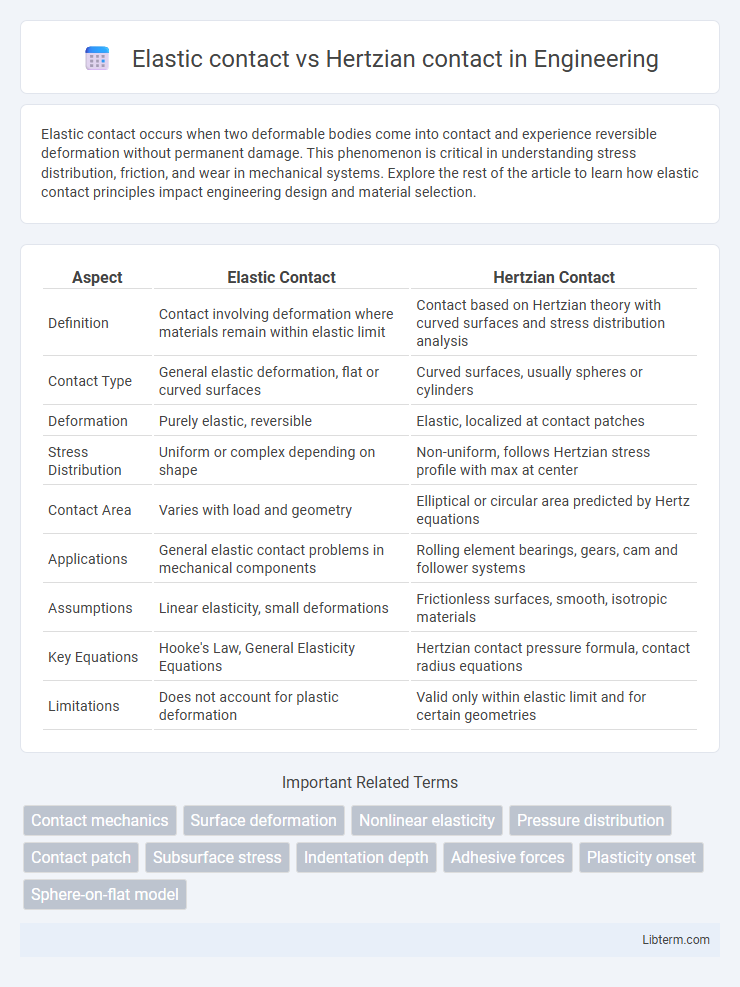
| Aspect | Elastic Contact | Hertzian Contact |
|---|---|---|
| Definition | Contact involving deformation where materials remain within elastic limit | Contact based on Hertzian theory with curved surfaces and stress distribution analysis |
| Contact Type | General elastic deformation, flat or curved surfaces | Curved surfaces, usually spheres or cylinders |
| Deformation | Purely elastic, reversible | Elastic, localized at contact patches |
| Stress Distribution | Uniform or complex depending on shape | Non-uniform, follows Hertzian stress profile with max at center |
| Contact Area | Varies with load and geometry | Elliptical or circular area predicted by Hertz equations |
| Applications | General elastic contact problems in mechanical components | Rolling element bearings, gears, cam and follower systems |
| Assumptions | Linear elasticity, small deformations | Frictionless surfaces, smooth, isotropic materials |
| Key Equations | Hooke's Law, General Elasticity Equations | Hertzian contact pressure formula, contact radius equations |
| Limitations | Does not account for plastic deformation | Valid only within elastic limit and for certain geometries |
Introduction to Contact Mechanics
Contact mechanics studies the deformation and stress between two bodies in contact, fundamental in both elastic and Hertzian contact models. Elastic contact assumes the materials deform elastically under load, with stress distribution dependent on the material's elastic modulus and geometry. Hertzian contact specifically describes non-adhesive contact between curved surfaces, predicting contact area, pressure distribution, and deformation based on Hertz's theory, crucial for analyzing stresses in bearing and gear applications.
Defining Elastic Contact
Elastic contact refers to the interaction between two bodies where the materials deform reversibly under applied load, maintaining their original shape upon load removal, governed by Hooke's law and characterized by stress and strain within the elastic limit. Hertzian contact is a specific type of elastic contact involving curved surfaces, where stress distribution follows Hertz's theory, predicting contact area and pressure with no plastic deformation. Defining elastic contact emphasizes material elasticity, linear stress-strain relationships, and the absence of permanent deformation during loading and unloading cycles.
Foundations of Hertzian Contact Theory
Hertzian contact theory is based on elastic contact mechanics describing the stress and deformation between two curved surfaces in contact, assuming small strains and linear elasticity. It provides analytical solutions for contact area, pressure distribution, and deformation, relying on material properties like Young's modulus and Poisson's ratio. The theory applies primarily to non-adhesive, frictionless contact between isotropic, homogeneous solids, forming a foundation for analyzing load transfer in mechanical components such as bearings and gears.
Key Differences: Elastic vs. Hertzian Contact
Elastic contact involves deformation of contacting bodies that can be fully recovered upon load removal, governed by generalized elasticity theory, while Hertzian contact specifically describes the localized stress and deformation between two curved surfaces under load based on Hertzian contact mechanics. Key differences include the scope of contact models, where elastic contact covers broader material behaviors and shapes, whereas Hertzian contact precisely quantifies contact area, pressure distribution, and deformation for non-conforming bodies like spheres or cylinders. Hertzian contact typically assumes frictionless, smooth surfaces and linear elasticity, focusing on stress concentration and contact patch size, contrasting with the more comprehensive elastic contact framework applicable to various geometries and loading conditions.
Material Properties Affecting Contact
Elastic contact considers the deformation of materials based on their elastic moduli and Poisson's ratios, which directly influence the contact area and stress distribution. Hertzian contact theory assumes purely elastic behavior and uses these material properties to calculate the contact pressures and deformation without accounting for plasticity or material imperfections. Variations in Young's modulus and hardness significantly affect the load-bearing capacity and the extent of contact deformation in both models.
Load Distribution in Elastic and Hertzian Contacts
Load distribution in elastic contact involves the deformation of contacting surfaces, allowing the load to spread over a larger area and reduce stress concentrations, typically following the theory of linear elasticity. Hertzian contact specifically describes the localized stress distribution between curved surfaces under load, where contact stresses are highest at the center and decrease towards the edges, leading to a characteristic elliptical or circular contact area. Understanding these load distribution patterns is critical for predicting material behavior and preventing failure in mechanical components subjected to contact stresses.
Mathematical Models for Each Contact Type
Elastic contact is typically modeled using Hertzian contact theory, which describes the stress distribution and deformation between two elastic bodies in contact, relying on assumptions of small deformations and linearly elastic materials. The Hertzian model uses parameters such as the radii of curvature, elastic moduli, and Poisson's ratios to calculate contact radius, pressure distribution, and indentation depth through nonlinear equations. In contrast, generalized elastic contact models may incorporate factors like plastic deformation or friction, extending beyond Hertzian assumptions and employing numerical methods like finite element analysis to solve more complex boundary conditions and material behaviors.
Applications in Engineering and Industry
Elastic contact theory is crucial in designing machine components such as gears, rolling element bearings, and cam-follower systems, where accurate prediction of stress distribution ensures durability under repetitive loads. Hertzian contact theory is extensively applied in tribology and materials testing, facilitating the analysis of contact stresses and deformation in applications like tire-road interaction, metal forming processes, and ball bearing design. Both theories enable engineers to optimize performance and longevity by accurately modeling contact mechanics in automotive, aerospace, and manufacturing industries.
Limitations and Assumptions of Each Approach
Hertzian contact theory assumes purely elastic deformation, small contact areas relative to object sizes, and isotropic, homogeneous materials, limiting its accuracy under plastic deformation or anisotropic conditions. Elastic contact models extend beyond Hertzian assumptions by accommodating nonlinear material behavior, larger deformations, and time-dependent properties, but they often require complex numerical methods like finite element analysis. Both approaches overlook surface roughness and friction effects, which can significantly influence real-world contact mechanics and stress distributions.
Conclusion: Choosing the Right Contact Model
Selecting the appropriate contact model hinges on the specific application requirements and loading conditions. Elastic contact models provide a more accurate representation of real-world behavior under moderate loads by accounting for material deformation and stress distribution, while Hertzian contact theory offers simplified calculations ideal for preliminary design and cases with small deformations. Engineers must balance the need for precision with computational efficiency to optimize component reliability and performance.
Elastic contact Infographic
 libterm.com
libterm.com