Finite Element Method (FEM) is a numerical technique widely used for solving complex engineering and physical problems by breaking down structures into smaller, manageable elements. This method enhances accuracy and efficiency in analyzing stresses, heat transfer, and fluid dynamics within diverse systems. Discover how FEM can optimize your design and analysis by exploring the detailed insights in this article.
Table of Comparison
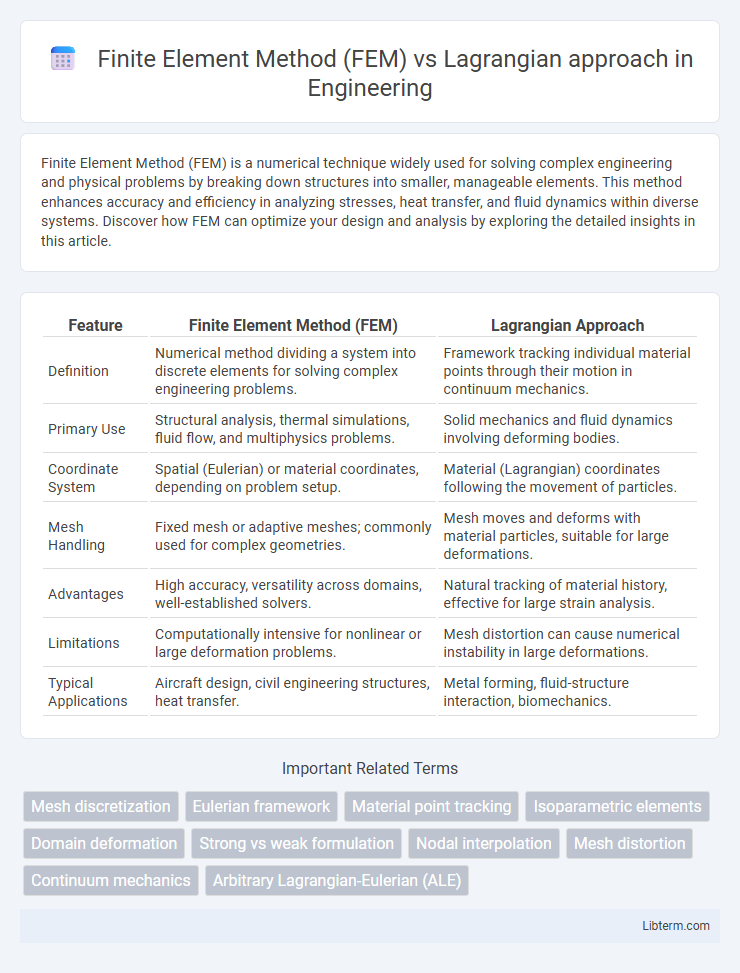
| Feature | Finite Element Method (FEM) | Lagrangian Approach |
|---|---|---|
| Definition | Numerical method dividing a system into discrete elements for solving complex engineering problems. | Framework tracking individual material points through their motion in continuum mechanics. |
| Primary Use | Structural analysis, thermal simulations, fluid flow, and multiphysics problems. | Solid mechanics and fluid dynamics involving deforming bodies. |
| Coordinate System | Spatial (Eulerian) or material coordinates, depending on problem setup. | Material (Lagrangian) coordinates following the movement of particles. |
| Mesh Handling | Fixed mesh or adaptive meshes; commonly used for complex geometries. | Mesh moves and deforms with material particles, suitable for large deformations. |
| Advantages | High accuracy, versatility across domains, well-established solvers. | Natural tracking of material history, effective for large strain analysis. |
| Limitations | Computationally intensive for nonlinear or large deformation problems. | Mesh distortion can cause numerical instability in large deformations. |
| Typical Applications | Aircraft design, civil engineering structures, heat transfer. | Metal forming, fluid-structure interaction, biomechanics. |
Introduction to Finite Element Method (FEM) and Lagrangian Approach
The Finite Element Method (FEM) is a numerical technique used for solving complex engineering and physical problems by discretizing a continuous domain into smaller, manageable elements. The Lagrangian approach, integral to FEM, tracks individual material points as they move through space and time, making it essential for problems involving large deformations and material history dependence. Combining FEM with the Lagrangian formulation enables precise modeling of structural behavior, fluid-structure interactions, and nonlinear dynamics.
Fundamental Principles of FEM
The Finite Element Method (FEM) divides complex structures into smaller, manageable elements, using variational principles like the principle of minimum potential energy to derive approximate solutions to differential equations. FEM relies on discretization and interpolation functions to transform continuum problems into algebraic equations, enabling numerical solution for stress, strain, and displacement fields. In contrast, the Lagrangian approach follows individual material points through deformation, emphasizing equations of motion derived from Lagrange's equations in classical mechanics.
Core Concepts of the Lagrangian Approach
The Lagrangian approach in computational mechanics tracks the motion of individual particles or elements by following their trajectories through time, maintaining a fixed reference frame attached to the material. This method inherently captures material deformation and history-dependent behaviors, making it ideal for problems involving large strains and complex material responses. In contrast to the Eulerian perspective often used in fluid dynamics, the Lagrangian framework simplifies the formulation of governing equations for solids by focusing on displacement fields relative to the original configuration.
Mathematical Formulation in FEM vs Lagrangian Approach
The Finite Element Method (FEM) relies on discretizing the domain into smaller elements and formulating a system of algebraic equations derived from partial differential equations using variational principles or the Galerkin method. The Lagrangian approach in mechanics uses generalized coordinates to describe the system's configuration, forming equations of motion through the Euler-Lagrange equations based on kinetic and potential energy functionals. While FEM transforms continuous problems into solvable algebraic systems via mesh-dependent shape functions, the Lagrangian method emphasizes energy-based scalar functions without explicit spatial discretization.
Mesh Generation and Adaptivity: FEM vs Lagrangian Methods
Finite Element Method (FEM) relies on structured or unstructured mesh generation which precisely discretizes the domain into elements, allowing for systematic mesh refinement and adaptivity based on error estimates. Lagrangian methods track material points and often bypass fixed mesh requirements, enabling natural adaptivity to deforming geometries but posing challenges for maintaining mesh quality over large deformations. Mesh adaptivity in FEM is enhanced through h-, p-, and r-refinement techniques, while Lagrangian approaches focus on particle repositioning and remeshing strategies to handle evolving domains effectively.
Application Areas: Where FEM and Lagrangian Excel
Finite Element Method (FEM) excels in structural analysis, thermal simulations, and fluid dynamics, particularly for complex geometries and boundary conditions in aerospace, automotive, and civil engineering. The Lagrangian approach is preferred in particle tracking, fluid-structure interaction, and material deformation studies, offering precise mesh movement representation in biomechanics and manufacturing processes. Both methods complement each other, with FEM providing mesh-based discretization and Lagrangian delivering accurate motion description in dynamic systems.
Computational Complexity and Performance Comparison
Finite Element Method (FEM) typically involves solving large sparse systems of equations, resulting in computational complexity that scales with mesh density and element order, often leading to high resource demands for fine discretizations. The Lagrangian approach, especially in particle-based simulations, reduces complexity by tracking material points directly, which can improve performance in problems with large deformations but incurs overhead in updating neighbor lists and handling mesh entanglement. Performance comparison reveals FEM excels in structured problems with static meshes due to optimized linear solvers, whereas the Lagrangian approach offers advantages in nonlinear dynamics by avoiding remeshing costs but may suffer from increased memory usage and computational overhead in managing discrete elements.
Strengths and Limitations of Each Approach
The Finite Element Method (FEM) excels in handling complex geometries and boundary conditions with high accuracy through mesh discretization, yet it can be computationally intensive and sensitive to mesh quality. The Lagrangian approach efficiently tracks material deformation and history-dependent behaviors, making it ideal for problems involving large strains and moving boundaries, but it may suffer from mesh distortion and requires remeshing strategies for long-term simulations. Both methods provide critical tools for structural analysis and mechanical simulations, with FEM favored for static and linear problems and Lagrangian methods preferred in nonlinear, dynamic, or fluid-structure interaction scenarios.
Case Studies and Real-world Examples
Case studies comparing the Finite Element Method (FEM) and the Lagrangian approach reveal distinct advantages in structural analysis and fluid dynamics, respectively. In automotive crash simulations, FEM effectively models material deformation and stress distribution, while the Lagrangian approach excels in tracking individual particle trajectories in fluid-structure interactions. Real-world examples include FEM's use in aerospace component stress testing and the Lagrangian method's application in sediment transport modeling in environmental engineering.
Choosing the Right Method: FEM or Lagrangian Approach?
Choosing between the Finite Element Method (FEM) and the Lagrangian approach depends on the problem's complexity and the desired accuracy in simulating physical systems. FEM excels in handling complex geometries and boundary conditions by discretizing the domain into smaller elements, making it ideal for structural analysis, thermal simulations, and fluid dynamics. The Lagrangian approach, centered on tracking individual particles or elements through space and time, is particularly beneficial for problems involving large deformations, material history, or fluid-structure interaction where precise motion tracking is critical.
Finite Element Method (FEM) Infographic
 libterm.com
libterm.com