Simple harmonic motion describes the repetitive oscillation of an object about an equilibrium position, characterized by a restoring force proportional to its displacement. This motion is fundamental in physics, appearing in systems such as pendulums, springs, and even sound waves, where energy is transferred efficiently between kinetic and potential forms. Discover how understanding simple harmonic motion can deepen your grasp of natural phenomena by exploring the detailed principles outlined in this article.
Table of Comparison
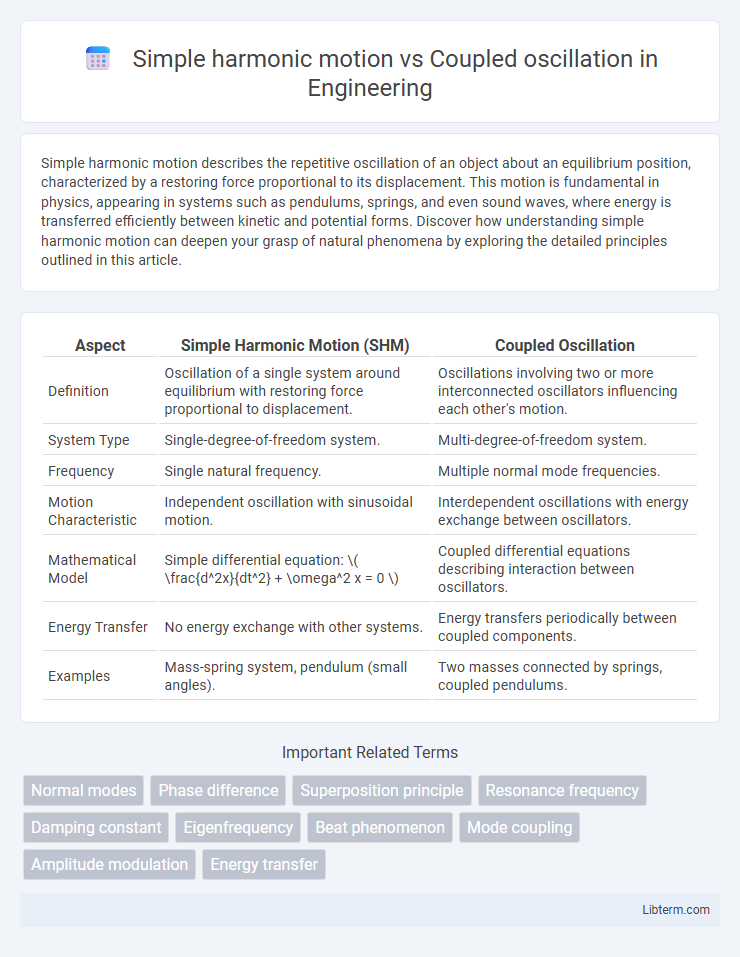
| Aspect | Simple Harmonic Motion (SHM) | Coupled Oscillation |
|---|---|---|
| Definition | Oscillation of a single system around equilibrium with restoring force proportional to displacement. | Oscillations involving two or more interconnected oscillators influencing each other's motion. |
| System Type | Single-degree-of-freedom system. | Multi-degree-of-freedom system. |
| Frequency | Single natural frequency. | Multiple normal mode frequencies. |
| Motion Characteristic | Independent oscillation with sinusoidal motion. | Interdependent oscillations with energy exchange between oscillators. |
| Mathematical Model | Simple differential equation: \( \frac{d^2x}{dt^2} + \omega^2 x = 0 \) | Coupled differential equations describing interaction between oscillators. |
| Energy Transfer | No energy exchange with other systems. | Energy transfers periodically between coupled components. |
| Examples | Mass-spring system, pendulum (small angles). | Two masses connected by springs, coupled pendulums. |
Introduction to Oscillatory Motion
Simple harmonic motion (SHM) describes oscillations where a single restoring force acts proportional to displacement, generating sinusoidal motion with constant amplitude and frequency. Coupled oscillation involves two or more interacting oscillators linked by forces, producing complex motion patterns such as normal modes and beat frequencies. Both phenomena are fundamental in studying oscillatory motion, revealing principles of energy exchange and resonance in mechanical and physical systems.
Fundamentals of Simple Harmonic Motion
Simple harmonic motion (SHM) is characterized by a restoring force proportional to displacement, resulting in periodic oscillations with constant amplitude and frequency, fundamental to understanding mechanical vibrations. Coupled oscillations arise when two or more SHM systems interact, causing energy transfer and complex motion patterns including beat phenomena and mode splitting. The fundamentals of SHM include Hooke's law, angular frequency o = (k/m), and sinusoidal displacement x(t) = A cos(ot + ph), providing the basis for analyzing more complex coupled systems.
Key Characteristics of Coupled Oscillation
Coupled oscillation occurs when two or more oscillators are linked so that energy exchanges between them, leading to complex motion patterns unlike the single-frequency oscillations seen in simple harmonic motion. Key characteristics include the presence of normal modes, where all parts of the system oscillate with the same frequency and fixed phase relations, and the phenomenon of beat frequencies resulting from energy transfer. This interaction causes variable amplitude and frequency combinations, distinguishing coupled oscillations from the uniform sinusoidal motion of simple harmonic oscillators.
Mathematical Representation: SHM vs Coupled System
Simple harmonic motion (SHM) is mathematically represented by the equation \( x(t) = A \cos(\omega t + \phi) \), where \( \omega = \sqrt{\frac{k}{m}} \) denotes the angular frequency for a single oscillator with mass \( m \) and spring constant \( k \). Coupled oscillations involve a system of differential equations characterizing multiple masses interconnected by springs, leading to normal modes described by eigenvalues and eigenvectors of the system's dynamical matrix. The mathematical complexity of coupled oscillations arises from solving these matrix equations to find distinct angular frequencies and mode shapes, contrasting with the simple sinusoidal form of SHM.
Energy Transfer in Both Oscillation Types
Simple harmonic motion (SHM) involves periodic energy transfer between kinetic and potential energy within a single oscillator, maintaining constant total mechanical energy. Coupled oscillations feature energy transfer between multiple oscillators through interaction forces, leading to energy exchange that causes complex motion patterns such as beats. In coupled oscillations, the continuous flow of energy between oscillators results in mode splitting and varying amplitudes, unlike the isolated, consistent energy exchange in SHM.
Phase Relationship and Synchronization
Simple harmonic motion involves a single oscillating system with a constant phase difference between displacement and velocity, maintaining a consistent sinusoidal pattern. Coupled oscillation features multiple interacting oscillators that exchange energy, resulting in complex phase relationships where oscillators may synchronize in phase or exhibit phase shifts leading to beats or mode splitting. Synchronization in coupled oscillations arises from the coupling strength, causing the oscillators to lock phases or oscillate with a constant phase difference, in contrast to the isolated phase behavior of simple harmonic motion.
Real-World Examples: SHM and Coupled Oscillators
Simple harmonic motion (SHM) is exemplified by a mass-spring system or a pendulum swinging with a consistent amplitude and frequency, demonstrating periodic oscillations in mechanical clocks or vehicle suspension systems. Coupled oscillations occur when two or more oscillators, such as pendulum clocks mounted on the same wall or coupled LC circuits in electronics, interact and exchange energy, resulting in complex motion patterns like beats or synchronized oscillations. Real-world applications of SHM and coupled oscillators include vibration analysis in structural engineering, synchronization of metronomes, and signal processing in communication technologies.
Similarities and Differences: Comparative Analysis
Simple harmonic motion (SHM) and coupled oscillations both involve periodic motion with restoring forces proportional to displacement, exhibiting sinusoidal waveforms and predictable frequencies. SHM describes a single oscillating system like a mass-spring or pendulum, characterized by a single natural frequency, whereas coupled oscillations occur in systems with two or more interacting oscillators, leading to multiple normal modes and frequency splitting. The primary difference lies in complexity: SHM focuses on isolated oscillators with uniform motion, while coupled oscillations showcase energy transfer between oscillators and complex dynamic behavior due to coupling forces.
Applications in Science and Engineering
Simple harmonic motion underpins the fundamental analysis of vibrating systems in mechanical engineering, such as pendulums and springs used in timekeeping devices and seismic sensors. Coupled oscillations model interactions in complex systems like molecular vibrations in chemistry and the behavior of electrical circuits with interconnected inductors and capacitors. Both phenomena are essential in designing stable structures, optimizing signal processing in telecommunications, and advancing materials science through resonance analysis.
Summary and Future Perspectives
Simple harmonic motion (SHM) describes the periodic oscillation of a single system around an equilibrium position with a restoring force proportional to displacement, while coupled oscillations involve two or more interacting oscillators influencing each other's motion. Advancements in nanotechnology and quantum mechanics provide promising avenues for exploiting coupled oscillations in precision sensing, signal processing, and quantum information systems. Future research aims to optimize energy transfer mechanisms and investigate nonlinear dynamics in coupled systems to enhance their functionality and control.
Simple harmonic motion Infographic
 libterm.com
libterm.com