Finite element analysis (FEA) is a powerful computational method used to predict how structures and materials respond to external forces, heat, and other physical effects by subdividing them into smaller, manageable elements. This technique enhances the accuracy of simulations in engineering design, failure analysis, and product optimization. Discover how mastering FEA can improve your projects by exploring the detailed insights in the rest of this article.
Table of Comparison
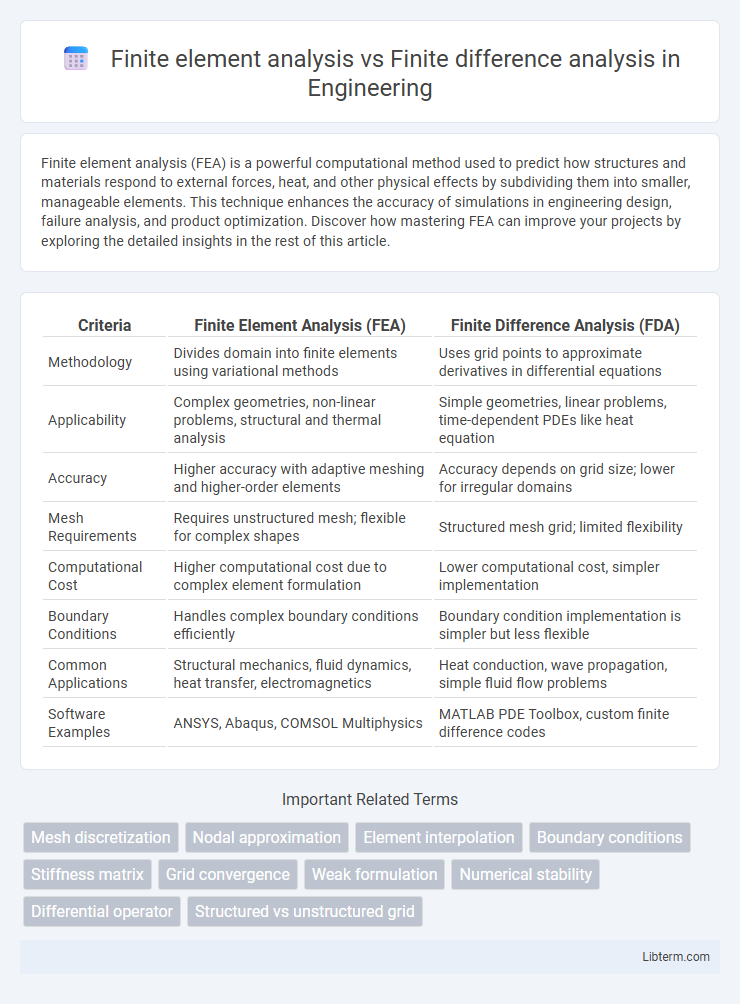
| Criteria | Finite Element Analysis (FEA) | Finite Difference Analysis (FDA) |
|---|---|---|
| Methodology | Divides domain into finite elements using variational methods | Uses grid points to approximate derivatives in differential equations |
| Applicability | Complex geometries, non-linear problems, structural and thermal analysis | Simple geometries, linear problems, time-dependent PDEs like heat equation |
| Accuracy | Higher accuracy with adaptive meshing and higher-order elements | Accuracy depends on grid size; lower for irregular domains |
| Mesh Requirements | Requires unstructured mesh; flexible for complex shapes | Structured mesh grid; limited flexibility |
| Computational Cost | Higher computational cost due to complex element formulation | Lower computational cost, simpler implementation |
| Boundary Conditions | Handles complex boundary conditions efficiently | Boundary condition implementation is simpler but less flexible |
| Common Applications | Structural mechanics, fluid dynamics, heat transfer, electromagnetics | Heat conduction, wave propagation, simple fluid flow problems |
| Software Examples | ANSYS, Abaqus, COMSOL Multiphysics | MATLAB PDE Toolbox, custom finite difference codes |
Introduction to Finite Element and Finite Difference Analysis
Finite Element Analysis (FEA) uses discretization of complex structures into smaller elements to approximate solutions for engineering problems involving stress, heat transfer, and fluid flow. Finite Difference Analysis (FDA) approximates differential equations by replacing derivatives with difference equations on a grid, often applied to solve partial differential equations numerically. Both methods transform continuous domain problems into discrete models but differ in mesh structure and formulation, with FEA favored for complex geometries and FDA for simpler, structured grids.
Fundamental Principles and Concepts
Finite element analysis (FEA) divides complex structures into smaller, simpler parts called finite elements, using interpolation functions to approximate solutions of differential equations over these elements. Finite difference analysis (FDA) approximates derivatives by replacing them with difference quotients on a discrete grid, directly solving differential equations at grid points. FEA excels in handling complex geometries and boundary conditions through mesh flexibility, whereas FDA is typically applied to problems with regular domains and structured grids.
Mathematical Formulation: FEA vs FDA
Finite Element Analysis (FEA) employs a variational approach, discretizing a domain into elements and using shape functions to approximate solutions of partial differential equations, transforming them into a system of algebraic equations. Finite Difference Analysis (FDA) relies on approximating derivatives through difference quotients on a structured grid, converting differential operators into finite difference equations based on Taylor series expansions. FEA offers greater flexibility in handling complex geometries and boundary conditions due to its piecewise polynomial interpolation, whereas FDA is generally simpler but limited to regular grids and straightforward domains.
Discretization Techniques in Both Methods
Finite element analysis (FEA) employs mesh-based discretization using elements such as triangles or quadrilaterals to divide complex geometries into smaller, manageable units for numerical approximation. Finite difference analysis (FDA) discretizes the problem domain by approximating derivatives at grid points arranged in a structured lattice, primarily suited for regular geometries and uniform grids. The mesh flexibility in FEA allows for better handling of irregular boundaries, whereas FDA's structured grid approach offers simplicity but less geometric adaptability.
Strengths and Limitations of Finite Element Analysis
Finite Element Analysis (FEA) excels in handling complex geometries and varying boundary conditions through mesh generation, making it highly effective for structural, thermal, and fluid simulations. Its main limitation lies in computational intensity and the potential for inaccurate results if mesh quality or element selection is poor. Unlike Finite Difference Analysis, which is more straightforward for regular grids and simpler problems, FEA offers greater flexibility but demands higher computational resources and expertise.
Strengths and Limitations of Finite Difference Analysis
Finite Difference Analysis (FDA) excels in solving partial differential equations on structured grids with straightforward implementation, making it efficient for problems involving heat transfer and fluid dynamics. However, FDA struggles with complex geometries and irregular boundaries, limiting its applicability compared to Finite Element Analysis (FEA), which handles unstructured meshes and intricate shapes more effectively. Accuracy in FDA depends heavily on grid resolution, and it can suffer from numerical instability and reduced flexibility in modeling material heterogeneity.
Typical Applications and Industry Use Cases
Finite element analysis (FEA) excels in structural mechanics, aerospace engineering, and automotive design for stress, strain, and thermal simulations due to its ability to handle complex geometries and boundary conditions. Finite difference analysis (FDA) is commonly applied in fluid dynamics, heat transfer, and electromagnetic field simulations, particularly favored in geophysics and meteorology for solving partial differential equations over structured grids. Industries like civil engineering, biomechanics, and electronics heavily rely on FEA, while FDA is prominent in climate modeling, seismic analysis, and computational fluid dynamics research.
Accuracy and Computational Efficiency Comparison
Finite element analysis (FEA) offers higher accuracy in handling complex geometries and boundary conditions due to its flexible mesh refinement and variational formulation, whereas finite difference analysis (FDA) is generally simpler but less precise for irregular shapes. FEA computational efficiency can be lower because of its intensive matrix assembly and solution processes, while FDA benefits from straightforward grid-based computations, making it faster for problems with simple domains. Optimal method selection depends on the trade-off between the need for detailed precision in engineering simulations and available computational resources.
Software Tools for FEA and FDA
Popular software tools for Finite Element Analysis (FEA) include ANSYS, Abaqus, and COMSOL Multiphysics, offering comprehensive meshing capabilities and advanced solver options tailored for structural, thermal, and fluid dynamics problems. Finite Difference Analysis (FDA) often utilizes specialized platforms like MATLAB and custom-coded solutions due to its grid-based numerical approach, focusing on solving partial differential equations for problems such as heat transfer and wave propagation. While FEA software typically provides user-friendly interfaces and extensive libraries for material properties, FDA tools emphasize flexibility in discretization schemes and direct control over numerical algorithms.
Choosing the Right Method: Key Considerations
When choosing between finite element analysis (FEA) and finite difference analysis (FDA), consider the complexity of the geometry and boundary conditions, as FEA excels in handling irregular shapes and complex constraints with high precision. Material heterogeneity and nonlinear behavior are better addressed by FEA due to its flexible meshing capabilities, while FDA is efficient for simpler, structured grid problems with uniform properties. Computational resources and desired accuracy also influence the choice, with FDA often requiring less computational power for straightforward problems and FEA providing detailed results for intricate, real-world simulations.
Finite element analysis Infographic
 libterm.com
libterm.com