Uniform load refers to a consistent and evenly distributed force applied along the length of a structure, such as a beam or slab, which is crucial for accurate structural analysis and design. Understanding how uniform loads impact stress, deflection, and overall stability can help you ensure safety and performance in construction projects. Explore the rest of the article to learn more about calculating and managing uniform loads effectively.
Table of Comparison
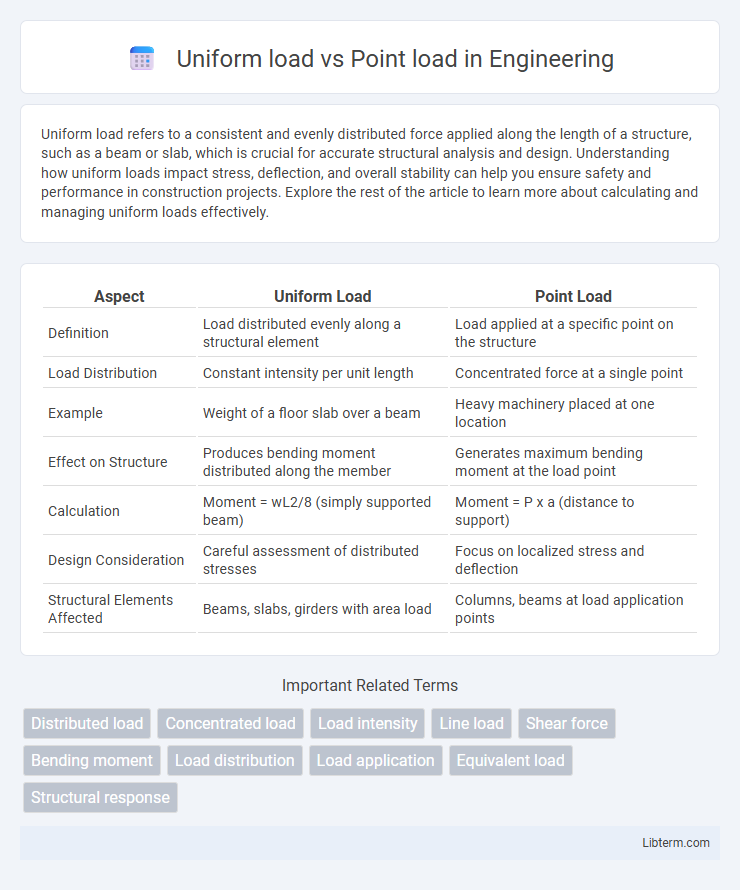
| Aspect | Uniform Load | Point Load |
|---|---|---|
| Definition | Load distributed evenly along a structural element | Load applied at a specific point on the structure |
| Load Distribution | Constant intensity per unit length | Concentrated force at a single point |
| Example | Weight of a floor slab over a beam | Heavy machinery placed at one location |
| Effect on Structure | Produces bending moment distributed along the member | Generates maximum bending moment at the load point |
| Calculation | Moment = wL2/8 (simply supported beam) | Moment = P x a (distance to support) |
| Design Consideration | Careful assessment of distributed stresses | Focus on localized stress and deflection |
| Structural Elements Affected | Beams, slabs, girders with area load | Columns, beams at load application points |
Introduction to Uniform and Point Loads
Uniform loads distribute force evenly over a surface, creating consistent pressure along the length of a beam or structure, essential for evaluating structural strength and deflection. Point loads concentrate force at a single location, generating high stress and localized bending moments that are critical in design calculations. Understanding the distinctions between uniform and point loads is fundamental for accurate structural analysis and safe engineering practices.
Definition of Uniform Load
A uniform load refers to a distribution of force applied consistently along the entire length or surface of a structural element, such as a beam or slab, resulting in equal load intensity per unit area or length. This type of load contrasts with a point load, which concentrates force at a single, specific location on the structure. Uniform loads are critical in engineering calculations for designing structures to ensure even stress distribution and stability under applied pressures.
Definition of Point Load
A point load refers to a concentrated force applied at a single, specific location on a structural element, causing localized stress and deformation. Unlike a uniform load, which is distributed evenly over a length or area, a point load produces a distinct bending moment and shear force at the application point. Engineers analyze point loads to determine critical stress points and design structural components to withstand concentrated forces efficiently.
Key Differences Between Uniform and Point Loads
Uniform loads distribute force evenly across a surface or length, commonly measured in pounds per square foot (psf) or newtons per meter (N/m), resulting in consistent stress along the structure. Point loads concentrate force at a single location, causing localized stress that requires reinforcement to prevent material failure or deformation. Structural analysis differs for each load type, with uniform loads often simplified using distributed load equations, while point loads demand precise calculation of bending moments and shear forces at specific points.
Effects on Structural Elements
Uniform load distributes force evenly along the length of the structural element, causing consistent bending moments and shear forces that promote predictable deflection patterns and stress distribution. Point load concentrates force at a single point, resulting in localized high stress, significant shear force peaks, and potential bending moment variations that can create stress concentrations and increased risk of structural failure. Engineers must analyze these load types carefully to design structural elements that withstand varying stress distributions and prevent localized damage or excessive deflection.
Real-World Examples of Uniform Loads
Uniform loads are common in real-world structures where weight is evenly spread across a surface, such as the weight of snow accumulating uniformly on a flat roof, the pressure exerted by soil on retaining walls, or the distributed weight of water in a swimming pool on the pool's floor. Unlike point loads, which are concentrated at a single location like a heavy machine resting on a small platform area, uniform loads create consistent stress along beams and structural elements, impacting design calculations for bending moments and shear forces. Engineers use these scenarios to ensure safety by calculating load distribution, material strength, and deflection limits for applications like floor slabs, bridge decks, and ship hulls.
Real-World Examples of Point Loads
Point loads concentrate force at a specific location, commonly seen in real-world scenarios such as a heavy machine placed on a single steel beam or the load from a column in building structures. Unlike uniform loads that distribute weight evenly, point loads cause higher stress concentrations that engineers must consider when designing supports and foundations. Examples include a crane's hook applying force to a beam or the impact of a vehicle's wheel on a bridge.
Calculation Methods for Each Load Type
Calculation methods for uniform load involve integrating the load intensity over the entire length of the beam, resulting in a distributed force commonly expressed in kN/m. In contrast, point load calculations focus on a single concentrated force applied at a specific location, requiring direct application of static equilibrium equations to determine reactions and internal moments. Beam deflection and stress under uniform load are typically computed using integral calculus or standard formulas for distributed loads, while point load analysis relies on moment and shear force equations at the load application point.
Importance in Structural Design
Uniform load and point load are critical factors in structural design because they determine stress distribution and deflection in beams and other structural elements. Uniform loads represent evenly distributed forces such as the weight of floors or roofs, ensuring consistent stress along a member, while point loads apply concentrated forces at specific locations, creating localized stress concentrations. Understanding the differences between these load types is essential for designing safe, efficient structures that resist bending, shear, and potential failure.
Conclusion: Choosing the Right Load Type
Selecting the appropriate load type depends on the structural application and load distribution requirements; uniform loads are ideal for evenly distributed forces such as roofing or flooring systems, ensuring consistent stress across the structure. Point loads concentrate force at a specific location, commonly used for columns or concentrated weights, necessitating reinforcement to prevent localized failure. Understanding load characteristics and structural capacity ensures optimal design efficiency and safety in engineering projects.
Uniform load Infographic
 libterm.com
libterm.com