Plane stress refers to a two-dimensional stress condition where the stress components perpendicular to a specific plane are negligible, commonly encountered in thin structures like plates or shells. This assumption simplifies complex three-dimensional stress analysis by focusing on in-plane stresses, which are crucial for accurate design and safety assessments in mechanical and civil engineering. Explore the rest of the article to understand how plane stress influences material behavior and structural integrity.
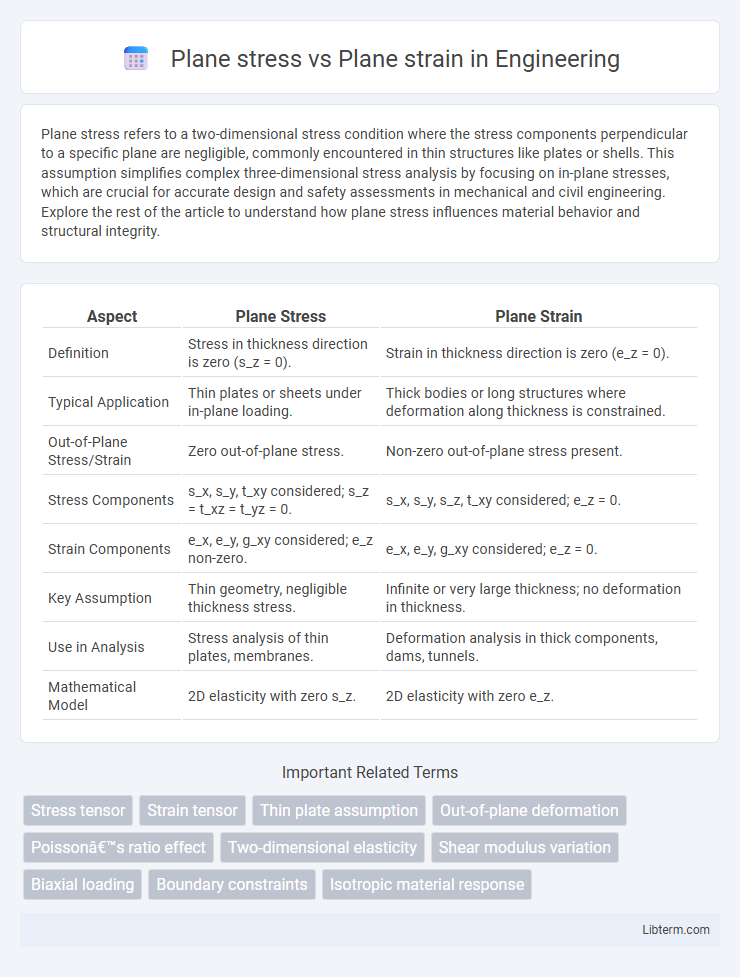
Table of Comparison
| Aspect | Plane Stress | Plane Strain |
|---|---|---|
| Definition | Stress in thickness direction is zero (s_z = 0). | Strain in thickness direction is zero (e_z = 0). |
| Typical Application | Thin plates or sheets under in-plane loading. | Thick bodies or long structures where deformation along thickness is constrained. |
| Out-of-Plane Stress/Strain | Zero out-of-plane stress. | Non-zero out-of-plane stress present. |
| Stress Components | s_x, s_y, t_xy considered; s_z = t_xz = t_yz = 0. | s_x, s_y, s_z, t_xy considered; e_z = 0. |
| Strain Components | e_x, e_y, g_xy considered; e_z non-zero. | e_x, e_y, g_xy considered; e_z = 0. |
| Key Assumption | Thin geometry, negligible thickness stress. | Infinite or very large thickness; no deformation in thickness. |
| Use in Analysis | Stress analysis of thin plates, membranes. | Deformation analysis in thick components, dams, tunnels. |
| Mathematical Model | 2D elasticity with zero s_z. | 2D elasticity with zero e_z. |
Introduction to Plane Stress and Plane Strain
Plane stress occurs in thin structures where stress through the thickness is negligible, typically in thin plates subjected to in-plane forces, making it ideal for 2D stress analysis. Plane strain describes deformation in long structures with uniform cross-section where strain along the length is zero, commonly applied in deep beams or dams. Both conditions simplify complex 3D stress states into manageable 2D models essential for structural and mechanical engineering calculations.
Fundamental Concepts and Definitions
Plane stress occurs when stress is assumed to be zero through the thickness of a thin object, typically in thin plates where out-of-plane stresses are negligible. Plane strain describes a condition where strain in one direction (usually thickness) is zero, common in long structures with constrained deformation, such as tunnels or dams. Both concepts simplify three-dimensional stress states into two dimensions, aiding in the analysis of mechanical behavior under specific geometric and loading conditions.
Mathematical Formulation of Plane Stress
Plane stress is mathematically formulated by assuming the stress component perpendicular to the plane, \(\sigma_z\), and the shear stresses involving the z-axis, \(\tau_{xz}\) and \(\tau_{yz}\), are zero, simplifying the three-dimensional stress tensor to a two-dimensional form. The constitutive relations under plane stress reduce to \(\sigma_x = \frac{E}{1-\nu^2} (\epsilon_x + \nu \epsilon_y)\), \(\sigma_y = \frac{E}{1-\nu^2} (\epsilon_y + \nu \epsilon_x)\), and \(\tau_{xy} = G \gamma_{xy}\), where \(E\) is Young's modulus, \(\nu\) is Poisson's ratio, and \(G\) is the shear modulus. This formulation enables solving elasticity problems in thin structures where thickness is small relative to in-plane dimensions, streamlining stress analysis with reduced computational complexity.
Mathematical Formulation of Plane Strain
Plane strain conditions assume zero strain in the thickness direction, simplifying the strain tensor to e_z = 0, which leads to e_xz = e_yz = 0, reducing the 3D elasticity problem to 2D. The stress-strain relationship under plane strain is expressed as s = De, where D is the stiffness matrix derived from Young's modulus (E) and Poisson's ratio (n), incorporating the constraint e_z = 0 through modified constitutive equations: s_x = [(1 - n) / ((1 + n)(1 - 2n))] E e_x + [n / ((1 + n)(1 - 2n))] E e_y, with similar forms for s_y and s_z. This formulation contrasts with plane stress by considering non-zero s_z generated due to zero strain in the thickness, reflecting the deformation constraints typical in thick bodies under load.
Key Differences Between Plane Stress and Plane Strain
Plane stress occurs when stresses perpendicular to the plane are negligible, typically in thin structures like metal sheets, while plane strain assumes negligible strain in the thickness direction, common in long tunnels or thick walls. The key difference lies in boundary conditions: plane stress has zero out-of-plane stress (sz 0), whereas plane strain has zero out-of-plane strain (ez 0). These assumptions influence stress-strain relations and affect calculations of deformation and failure analysis in mechanical and civil engineering applications.
Practical Engineering Applications
Plane stress conditions commonly occur in thin flat structures such as aircraft wings and metal sheets where thickness is small compared to other dimensions, allowing out-of-plane stresses to be negligible. Plane strain applies predominantly in long structures like tunnels, dams, and deep foundations where deformation along the length is constrained, resulting in zero strain in that direction. Engineers select plane stress analysis for thin components under surface loads and plane strain analysis for thick bodies subjected to in-depth pressure to optimize design accuracy and material utilization.
Assumptions and Limitations
Plane stress assumes that stress components perpendicular to the plane are negligible, making it suitable for thin structures subjected to surface loads, while plane strain assumes zero strain perpendicular to the plane, ideal for long, thick bodies where deformation in one dimension is constrained. Limitations of plane stress include inaccurate results for thick materials where out-of-plane stresses are significant, whereas plane strain models fail to capture deformation effects in bodies that are not sufficiently long or restrained along the thickness direction. Both assumptions simplify three-dimensional stress states to two dimensions but must be carefully chosen based on geometry and loading to avoid erroneous stress and strain predictions.
Stress-Strain Relationships and Constitutive Equations
In plane stress conditions, stress components perpendicular to the plane are negligible, simplifying constitutive equations by reducing three-dimensional stress states to two-dimensional forms, typically used for thin structures like plates. Plane strain assumes zero strain in the out-of-plane direction, leading to different stress-strain relationships where transverse strains are constrained, common in thick bodies such as dams or tunnels. The generalized Hooke's law adapts to these scenarios by modifying stiffness matrices to reflect either zero out-of-plane stress (plane stress) or zero out-of-plane strain (plane strain), significantly affecting material response predictions in elastic analysis.
Numerical Modeling and Simulation Aspects
In numerical modeling and simulation, plane stress assumes zero stress in the thickness direction, ideal for thin structures like plates and shells, simplifying computations by reducing the 3D problem to 2D. Plane strain applies when deformation in the thickness direction is constrained, typical for long structures such as tunnels or dams, requiring simulations to consider strain along the out-of-plane axis for accurate results. Choosing between plane stress and plane strain models depends on the geometric and loading conditions, directly impacting the accuracy and computational efficiency of finite element analyses.
Summary and Conclusion
Plane stress occurs when the stress perpendicular to a material's surface is negligible, commonly found in thin structures like metal sheets. Plane strain describes a state where strain along one axis is minimal, typical in thick bodies or long structures such as dams and tunnels. Comparing both, plane stress is ideal for thin components under in-plane loads, while plane strain suits scenarios involving constrained deformation in one direction, guiding engineers in selecting appropriate models for structural analysis.
Plane stress Infographic
 libterm.com
libterm.com