Incompressible flow refers to fluid motion where the fluid density remains constant throughout the flow field, typically applicable to liquids and low-speed gas flows. This assumption simplifies the Navier-Stokes equations, making it easier to analyze velocity and pressure changes without density variations. Explore the rest of the article to understand how incompressible flow principles apply to your fluid dynamics challenges.
Table of Comparison
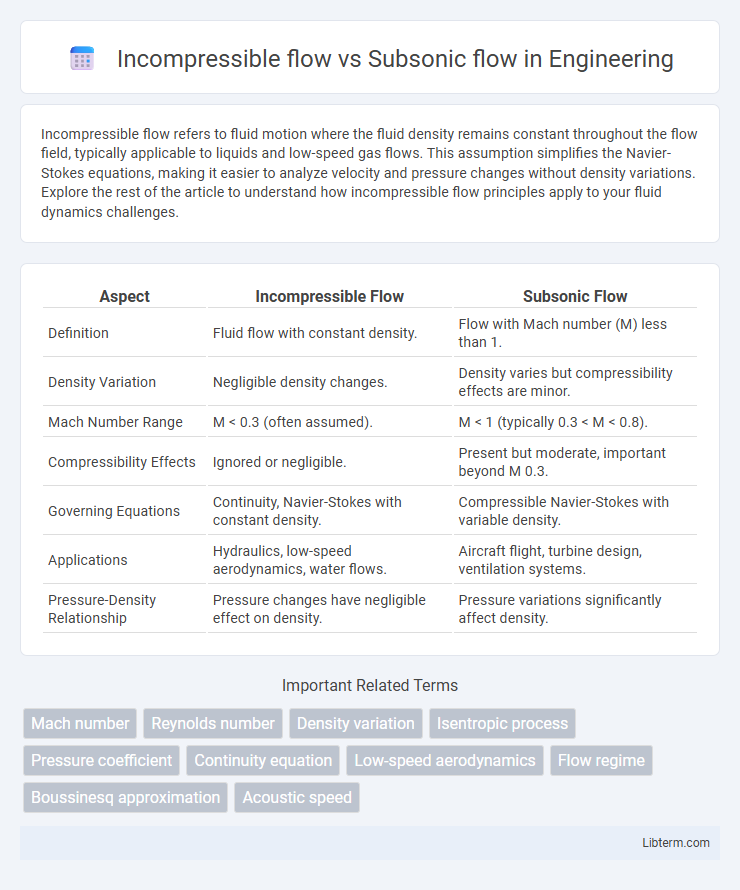
| Aspect | Incompressible Flow | Subsonic Flow |
|---|---|---|
| Definition | Fluid flow with constant density. | Flow with Mach number (M) less than 1. |
| Density Variation | Negligible density changes. | Density varies but compressibility effects are minor. |
| Mach Number Range | M < 0.3 (often assumed). | M < 1 (typically 0.3 < M < 0.8). |
| Compressibility Effects | Ignored or negligible. | Present but moderate, important beyond M 0.3. |
| Governing Equations | Continuity, Navier-Stokes with constant density. | Compressible Navier-Stokes with variable density. |
| Applications | Hydraulics, low-speed aerodynamics, water flows. | Aircraft flight, turbine design, ventilation systems. |
| Pressure-Density Relationship | Pressure changes have negligible effect on density. | Pressure variations significantly affect density. |
Introduction to Fluid Flow Regimes
Incompressible flow assumes constant fluid density and is typically applied to liquid flows or gas flows at low speeds where density changes are negligible, usually at Mach numbers below 0.3. Subsonic flow refers to fluid motion where the velocity is less than the speed of sound in the medium, encompassing a broader range of compressibility effects compared to purely incompressible flow. Understanding the distinction between these regimes is essential for accurate analysis and modeling of fluid behavior in aerodynamics, hydraulic systems, and HVAC applications.
Defining Incompressible Flow
Incompressible flow is characterized by a constant fluid density throughout the flow field, which simplifies the continuity equation by assuming density variations are negligible, typically valid for liquids and low-speed gas flows where Mach number is less than 0.3. Subsonic flow refers to fluid motion where the flow velocity is below the speed of sound, generally involving Mach numbers less than 1, and can exhibit both compressible and incompressible characteristics depending on velocity and fluid properties. Defining incompressible flow focuses on the negligible density variation assumption, which distinguishes it from subsonic flow that primarily emphasizes flow velocity relative to sound speed without explicitly assuming constant density.
Understanding Subsonic Flow
Subsonic flow occurs when the flow velocity is less than the speed of sound, typically characterized by a Mach number below 0.8, where compressibility effects are minimal but not entirely negligible. Unlike incompressible flow, which assumes constant density, subsonic flow requires accounting for slight density variations due to pressure changes, especially near aerodynamic surfaces. Understanding subsonic flow is crucial in designing aircraft and turbo machinery as it directly influences lift, drag, and pressure distribution around bodies moving through air.
Key Differences: Incompressible vs Subsonic Flow
Incompressible flow assumes constant fluid density and typically applies to low-speed liquids and gases with Mach numbers below 0.3, where compressibility effects are negligible. Subsonic flow, defined by Mach numbers less than 1 but can approach compressible regimes near Mach 0.8, allows for variable density and pressure changes within the flow field. The main difference lies in density variation, as incompressible flow treats density as constant, while subsonic flow accounts for density changes due to pressure and temperature variations.
Physical Assumptions and Mathematical Models
Incompressible flow assumes constant fluid density, simplifying the Navier-Stokes equations to neglect density variations and compressibility effects, typically valid for low-speed flows with Mach numbers below 0.3. Subsonic flow involves fluid speeds less than the speed of sound but allows variable density and pressure, requiring compressible flow equations like the full Navier-Stokes or Euler equations with state equations coupling pressure, density, and temperature. The key mathematical distinction lies in the continuity equation: incompressible flow uses a divergence-free velocity field, while subsonic flow requires coupled nonlinear partial differential equations accounting for density changes and thermodynamic properties.
Applications of Incompressible Flow Analysis
Incompressible flow analysis is crucial in hydraulic engineering, water supply systems, and aerodynamics of low-speed vehicles where density variations are negligible. It simplifies calculations for fluid motion in pipes, channels, and around aircraft wings operating well below the speed of sound. This approach enables efficient design and prediction of pressure drops, flow rates, and forces without accounting for compressibility effects typical in subsonic flow regimes near transonic speeds.
Applications of Subsonic Flow Analysis
Subsonic flow analysis is critical in the aerodynamic design of commercial aircraft, where airspeeds remain below the speed of sound to ensure stable lift and efficient fuel consumption. It is also extensively applied in HVAC systems to optimize airflow and maintain comfortable indoor environments. Additionally, subsonic flow principles govern the operation of wind turbines and automotive aerodynamics, enhancing performance and reducing drag.
Limitations and Critical Conditions
Incompressible flow assumes constant density, making it unsuitable for velocities approaching or exceeding the speed of sound due to significant compressibility effects. Subsonic flow, characterized by Mach numbers less than 1, allows density variations but experiences critical conditions near Mach 0.8 where compressibility becomes prominent and shock waves may form. The primary limitation of incompressible flow models lies in their inaccuracy for high-speed aerodynamics, while subsonic flow analysis must account for compressibility corrections to predict critical losses and flow separation accurately.
Real-World Engineering Examples
Incompressible flow is typically observed in liquid systems such as water distribution networks, where density changes are negligible, ensuring accurate pressure and velocity predictions. Subsonic flow occurs in applications like commercial aircraft wing aerodynamics, where airflow speeds remain below Mach 1, allowing for compressibility effects that influence lift and drag but do not cause shock waves. Engineering designs for hydraulic turbines rely on incompressible flow assumptions, while automotive and aerospace industries model subsonic airflow to optimize fuel efficiency and performance.
Summary and Comparative Insights
Incompressible flow assumes constant fluid density, typically valid for liquids and gases moving at Mach numbers below 0.3, while subsonic flow encompasses all flows with Mach numbers less than 1, where compressibility effects are mild but not negligible. Incompressible flow simplifies analysis by excluding density variations, whereas subsonic flow requires accounting for slight density changes affecting pressure and velocity fields. Engineers select incompressible models for low-speed fluid dynamics and use subsonic flow approaches for higher-speed aerodynamics where compressibility-starting effects influence performance and stability.
Incompressible flow Infographic
 libterm.com
libterm.com