A trace map is a visual representation used to track the flow of data or execution within a system, aiding in debugging and performance analysis. It highlights how different components interact and helps identify bottlenecks or errors efficiently. Explore the rest of the article to learn how to create and utilize trace maps effectively in your projects.
Table of Comparison
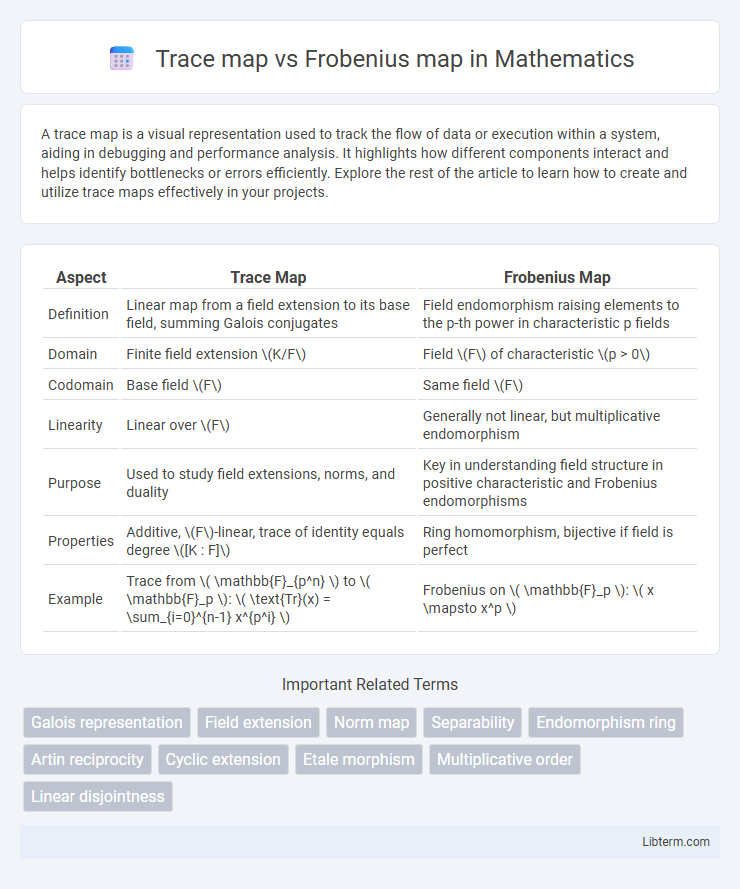
| Aspect | Trace Map | Frobenius Map |
|---|---|---|
| Definition | Linear map from a field extension to its base field, summing Galois conjugates | Field endomorphism raising elements to the p-th power in characteristic p fields |
| Domain | Finite field extension \(K/F\) | Field \(F\) of characteristic \(p > 0\) |
| Codomain | Base field \(F\) | Same field \(F\) |
| Linearity | Linear over \(F\) | Generally not linear, but multiplicative endomorphism |
| Purpose | Used to study field extensions, norms, and duality | Key in understanding field structure in positive characteristic and Frobenius endomorphisms |
| Properties | Additive, \(F\)-linear, trace of identity equals degree \([K : F]\) | Ring homomorphism, bijective if field is perfect |
| Example | Trace from \( \mathbb{F}_{p^n} \) to \( \mathbb{F}_p \): \( \text{Tr}(x) = \sum_{i=0}^{n-1} x^{p^i} \) | Frobenius on \( \mathbb{F}_p \): \( x \mapsto x^p \) |
Overview of Trace Map and Frobenius Map
The Trace map is a linear function from an extension field to its base field, capturing the sum of Galois conjugates and playing a key role in field theory and algebraic number theory. The Frobenius map, defined in fields of characteristic \(p\), is a field homomorphism raising each element to its \(p\)-th power, fundamental in the structure of finite fields and algebraic geometry. Both maps are instrumental in understanding field extensions, with the Trace map focusing on additive properties and the Frobenius map emphasizing multiplicative and automorphism structures.
Definitions and Mathematical Background
Trace map is a linear function from a field extension \(L/K\) to the base field \(K\), defined by summing the images of an element under all embeddings of \(L\) into an algebraic closure of \(K\). Frobenius map is an endomorphism in fields of positive characteristic \(p\), defined by raising each element to the \(p\)-th power, and it preserves the field structure. Both maps play crucial roles in algebraic number theory and finite field theory, with trace facilitating norm and discriminant calculations, while Frobenius captures Galois action in characteristic \(p\).
Historical Development and Context
The Frobenius map, introduced in the early 20th century, emerged as a fundamental tool in algebraic geometry and number theory, particularly in studying fields of positive characteristic. The trace map developed subsequently as a complementary concept, providing a linear functional that captures essential information from field extensions or endomorphisms, often used in the context of finite fields and Galois theory. Together, these maps have shaped modern approaches to understanding algebraic structures by revealing deep connections between field theory, cohomology, and arithmetic geometry.
Key Properties of the Trace Map
The trace map is a linear map from a field extension to its base field, defined by summing Galois conjugates, whereas the Frobenius map is an endomorphism in fields of characteristic p that raises elements to the p-th power. Key properties of the trace map include its linearity over the base field, non-degeneracy in finite separable extensions, and its role in defining the trace form, a symmetric bilinear form used in algebraic number theory and Galois theory. Unlike the Frobenius map, the trace map captures additive information about the extension and is fundamental in duality theories and norm computations.
Key Properties of the Frobenius Map
The Frobenius map in a field of characteristic p is a ring homomorphism defined by raising each element to the p-th power, preserving addition and multiplication structures crucial in finite fields and algebraic geometry. It is injective and surjective in perfect fields, making it an automorphism, and its fixed points correspond to the prime field of characteristic p. Unlike the trace map, which is additive and linear, the Frobenius map is nonlinear but multiplicative, playing a fundamental role in the structure of fields and Galois theory.
Comparative Analysis: Trace Map vs Frobenius Map
The trace map and Frobenius map serve distinct roles in field theory, particularly over finite fields of characteristic p. The Frobenius map raises each element to its p-th power, acting as a field automorphism that preserves arithmetic structure, while the trace map aggregates the sum of Galois conjugates, yielding a linear functional crucial for field extensions and character sums. The Frobenius map is fundamental for defining Frobenius endomorphisms and understanding fixed fields, whereas the trace map facilitates applications in algebraic coding theory, cryptography, and the study of bilinear forms through its linearity and non-degeneracy properties.
Applications in Algebraic Structures
The Trace map is essential in algebraic number theory and finite field theory for constructing norm and trace forms, enabling field extensions analysis and applications in coding theory. The Frobenius map, predominantly used in fields of characteristic p, is crucial for studying algebraic varieties over finite fields, as well as in the structure of Galois groups and modules over rings. Both maps facilitate the understanding of field automorphisms and are instrumental in computations of invariants in algebraic structures.
Significance in Finite Field Theory
Trace maps in finite field theory provide a linear function from an extension field to its base field, capturing essential field element relationships and enabling the construction of field invariants. Frobenius maps act as automorphisms raising elements to the power of the base field's characteristic, preserving the field structure and playing a critical role in understanding Galois groups of finite fields. Together, these maps underpin advanced algorithms for error-correcting codes and cryptographic systems by facilitating efficient computations and structural insights in finite fields.
Computational Aspects and Examples
The Trace map and Frobenius map are fundamental in finite field arithmetic, where the Trace map sums powers of the Frobenius automorphism, enabling efficient computation of element traces in extensions \(\mathbb{F}_{p^n}\). The Frobenius map, defined as \(x \mapsto x^p\), is a linear operator over \(\mathbb{F}_p\) and facilitates fast exponentiation via repeated squaring in characteristic \(p\) fields. In practical coding theory and cryptography, the Trace map compresses information from \(\mathbb{F}_{p^n}\) to \(\mathbb{F}_p\), while the Frobenius map aids in constructing minimal polynomials and optimized field arithmetic algorithms.
Recent Research and Open Problems
Recent research on Trace map and Frobenius map has emphasized their roles in algebraic geometry and number theory, particularly in understanding the structure of finite fields and arithmetic schemes. Advances include improved characterization of Frobenius endomorphisms in positive characteristic and deeper insights into trace map interactions with etale cohomology groups. Open problems remain regarding the precise determination of trace map kernels in complex algebraic varieties and the extension of Frobenius map applications to new cryptographic protocols and coding theory frameworks.
Trace map Infographic
 libterm.com
libterm.com