A chord consists of three or more notes played simultaneously, forming the harmonic foundation of music. Understanding chord structures and progressions enhances Your ability to create and interpret musical compositions effectively. Explore the rest of this article to deepen your knowledge of chords and their role in music theory.
Table of Comparison
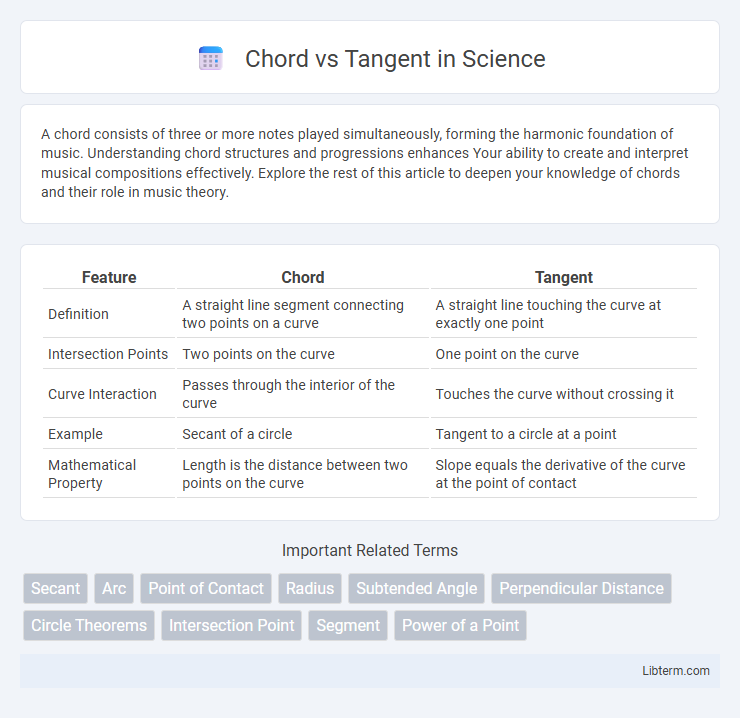
| Feature | Chord | Tangent |
|---|---|---|
| Definition | A straight line segment connecting two points on a curve | A straight line touching the curve at exactly one point |
| Intersection Points | Two points on the curve | One point on the curve |
| Curve Interaction | Passes through the interior of the curve | Touches the curve without crossing it |
| Example | Secant of a circle | Tangent to a circle at a point |
| Mathematical Property | Length is the distance between two points on the curve | Slope equals the derivative of the curve at the point of contact |
Introduction to Chord and Tangent
A chord is a line segment with both endpoints on the circumference of a circle, dividing the circle into two arcs. A tangent is a straight line that touches the circle at exactly one point, called the point of tangency, without crossing its interior. Understanding the geometric properties of chords and tangents is essential for solving circle-related problems in mathematics.
Definition of Chord
A chord is a straight line segment whose endpoints lie on the circumference of a circle, effectively dividing the circle into two arcs. It differs from a tangent, which touches the circle at exactly one point without crossing its interior. Understanding chords is fundamental in circle geometry, as they relate to properties such as arc lengths, central angles, and segment measures.
Definition of Tangent
A tangent to a circle is a straight line that touches the circle at exactly one point, known as the point of tangency, without crossing its boundary. Unlike a chord, which intersects the circle at two points, the tangent line only "grazes" the curve, maintaining perpendicularity to the radius drawn to the point of tangency. This unique property of tangents is fundamental in circle geometry and is widely used in calculus and trigonometry to determine slopes and limits.
Key Differences Between Chord and Tangent
A chord is a line segment with both endpoints on a circle, while a tangent is a line that touches the circle at exactly one point without crossing it. The key difference lies in their interaction with the circle: chords intersect the circle at two points, whereas tangents only make contact at a single point known as the point of tangency. Geometrically, the chord lies entirely inside the circle, whereas the tangent extends outside and just grazes the circle.
Geometric Properties of Chord
A chord is a line segment connecting two points on a curve, such as a circle, and its geometric properties include bisecting arcs and creating symmetrical segments within the circle. Unlike the tangent, which touches the curve at a single point without crossing it, the chord lies entirely inside the curve, dividing it into two distinct regions. The length of the chord can be determined using the radius and the central angle subtended by the chord, making it a fundamental element in circle geometry.
Geometric Properties of Tangent
The tangent to a circle touches the circle at exactly one point, called the point of tangency, and is perpendicular to the radius drawn to this point, establishing a unique angular relationship fundamental to circle geometry. Unlike chords, which intersect the circle at two points and lie entirely within the circle, tangents extend outside the circle without entering its interior, reflecting their distinct geometric role. This perpendicularity property is critical in solving problems involving angles, lengths, and circle constructions, making tangents essential in the study of Euclidean geometry and its applications.
Role of Chord and Tangent in Circles
A chord in a circle is a line segment connecting two points on the circle's circumference, playing a crucial role in defining arcs and creating inscribed angles. Tangents touch the circle at exactly one point, serving as perpendicular lines to the radius at the point of contact and defining the boundary without crossing the circle. Together, chords and tangents are fundamental in circle geometry, helping to establish relationships such as angle measures, segment lengths, and properties of cyclic quadrilaterals.
Real-Life Applications of Chords and Tangents
Chords and tangents are fundamental in engineering and navigation; chords help determine distances and midpoints in circular paths such as curved roads or bridges, while tangents are crucial for designing smooth vehicle turning angles and sensor placements in autonomous driving. In optics, tangents represent light rays touching curved mirrors or lenses at a single point, enabling precise image formation and laser targeting. Surveyors rely on chords to measure land plots with curved boundaries, ensuring accuracy in property delineation and construction layouts.
Common Misconceptions: Chord vs Tangent
A common misconception is that chords and tangents are interchangeable, but a chord is a line segment connecting two points on a circle, while a tangent touches the circle at exactly one point without crossing it. Many mistakenly believe a tangent can intersect the circle at two points, which contradicts its defining property of single-point contact. Understanding this distinction is crucial for solving geometry problems involving circles and their properties accurately.
Conclusion: Chord and Tangent Compared
A chord is a line segment connecting two points on a circle, whereas a tangent touches the circle at exactly one point without crossing it. The chord lies inside the circle, dividing it into two arcs, while the tangent only intersects the circle at the point of tangency, preventing any segment inside the circle. Understanding these distinctions clarifies their unique geometric properties and applications in circle theorems and constructions.
Chord Infographic
 libterm.com
libterm.com