A Binary Search Tree (BST) is a data structure that maintains elements in a sorted order, allowing efficient insertion, deletion, and search operations with average time complexity of O(log n). Each node has at most two children, with the left child containing values less than the parent and the right child containing values greater than the parent. Explore the rest of this article to understand how BSTs optimize data management and improve your algorithms.
Table of Comparison
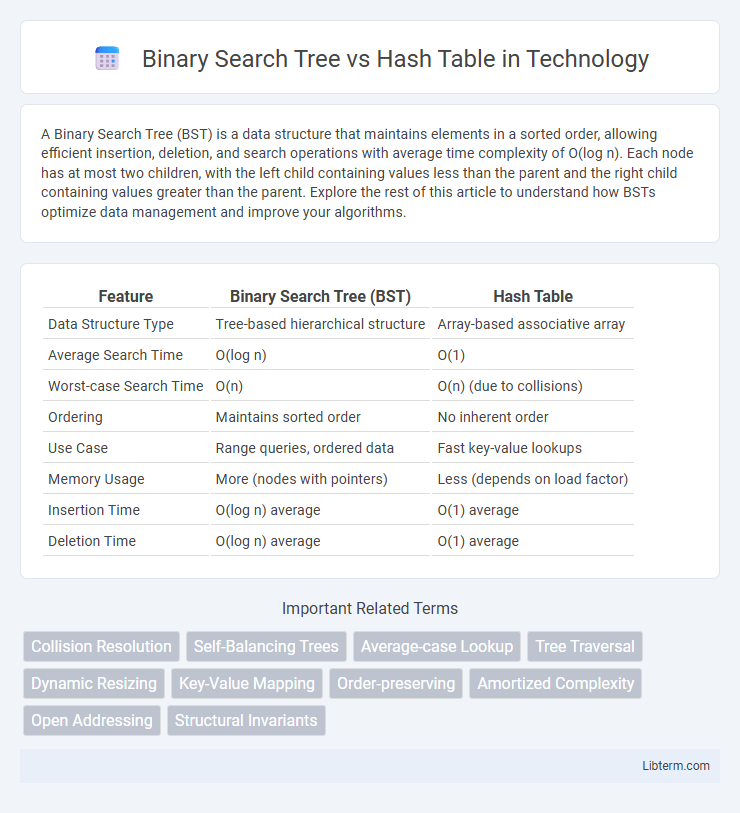
| Feature | Binary Search Tree (BST) | Hash Table |
|---|---|---|
| Data Structure Type | Tree-based hierarchical structure | Array-based associative array |
| Average Search Time | O(log n) | O(1) |
| Worst-case Search Time | O(n) | O(n) (due to collisions) |
| Ordering | Maintains sorted order | No inherent order |
| Use Case | Range queries, ordered data | Fast key-value lookups |
| Memory Usage | More (nodes with pointers) | Less (depends on load factor) |
| Insertion Time | O(log n) average | O(1) average |
| Deletion Time | O(log n) average | O(1) average |
Introduction to Binary Search Trees and Hash Tables
Binary Search Trees (BSTs) are hierarchical data structures that maintain sorted data, enabling efficient search, insertion, and deletion operations in average time complexity of O(log n). Hash Tables utilize a hash function to map keys to indices in an array, allowing average constant-time complexity O(1) for search, insert, and delete operations. While BSTs preserve data order and support range queries, Hash Tables excel in fast direct access without inherent ordering.
Core Concepts and Definitions
Binary Search Tree (BST) is a node-based data structure with ordered keys where each node has at most two children, ensuring left subtree values are less and right subtree values are greater, facilitating efficient logarithmic time search, insertion, and deletion in balanced trees. Hash Table is a key-value data structure using a hash function to compute an index into an array of buckets or slots, providing average constant time complexity for search, insert, and delete operations but with potential collisions managed by chaining or open addressing. BST maintains sorted data and supports in-order traversal, whereas Hash Tables excel in direct access without inherent order.
Data Structure Architecture
Binary Search Trees (BST) organize data hierarchically with nodes containing keys, enabling ordered traversal and efficient search with average time complexity O(log n) in balanced trees. Hash Tables use an array-based structure with a hash function to compute an index, providing average constant time complexity O(1) for insertions, deletions, and lookups but lack inherent order among elements. The architecture of BST supports range queries and sorted data retrieval while Hash Tables optimize direct access at the expense of memory overhead and potential collisions.
Insertion and Deletion Operations
Insertion in a Binary Search Tree (BST) involves traversing from the root to the appropriate leaf position, resulting in an average time complexity of O(log n) for balanced trees and O(n) in the worst case for unbalanced trees. Hash Table insertion relies on computing a hash function to determine the bucket location, achieving average-case constant time O(1) but can degrade to O(n) during collisions or resizing. Deletion in a BST requires finding the node, then restructuring the tree to maintain order, with complexities of O(log n) on average, whereas Hash Table deletion involves removing the key from the bucket and maintaining load factors, typically operating in O(1) time but affected by collision resolution methods.
Time Complexity Analysis
Binary Search Trees (BST) offer average-case search, insert, and delete operations with time complexity of O(log n) when balanced, but degrade to O(n) in the worst case due to tree skewness. Hash Tables provide average-case constant time complexity O(1) for search, insert, and delete operations, though worst-case scenarios can reach O(n) due to hash collisions. Performance depends on factors such as tree balancing techniques for BSTs and hash function quality and load factor management for Hash Tables.
Memory Usage and Space Efficiency
Binary Search Trees (BSTs) typically require more memory per node due to storage of pointers for left and right children, which can lead to higher overhead compared to hash tables. Hash tables allocate memory based on the size of the bucket array and handle stored elements more compactly, often providing better space efficiency for large datasets with low collision rates. However, the efficiency of a hash table's memory usage depends on the load factor and resizing strategy, whereas BSTs use memory more predictably but may become inefficient if unbalanced.
Search Performance Comparison
Binary Search Trees (BSTs) offer O(log n) average search time when balanced, relying on key ordering to efficiently navigate nodes. Hash Tables provide near O(1) average search time by computing a hash function to index entries directly, though worst-case performance can degrade to O(n) due to collisions. In scenarios requiring ordered data retrieval, BSTs outperform Hash Tables, but for pure search speed, well-implemented Hash Tables are typically superior.
Use Cases and Real-World Applications
Binary Search Trees (BSTs) are ideal for applications requiring ordered data access, such as database indexing, range queries, and in-memory sorting, allowing efficient logarithmic time complexity for search, insertion, and deletion operations. Hash Tables excel in scenarios demanding constant-time average lookups, like caching systems, symbol tables in compilers, and implementing associative arrays, where quick key-value pair access is crucial. Real-world applications favor BSTs for tasks involving sorted data traversal and balanced search operations, while Hash Tables are preferred for fast, direct access to data without order constraints.
Advantages and Disadvantages
Binary Search Trees (BST) provide ordered data storage, enabling efficient in-order traversal and range queries, with average-case time complexity of O(log n) for search, insertion, and deletion, but performance can degrade to O(n) in unbalanced cases. Hash Tables offer constant average-time complexity O(1) for search, insertion, and deletion, making them faster for exact key lookups, but they lack order, consume more memory due to hashing overhead, and suffer from collisions requiring complex resolution strategies. BSTs maintain sorted data and better support range-based queries, whereas Hash Tables excel in fast key-based access but are not suitable for operations requiring data ordering or range searches.
Choosing Between Binary Search Tree and Hash Table
Choosing between a Binary Search Tree (BST) and a Hash Table depends on the use case and data structure requirements. BSTs provide ordered traversal, efficient range queries, and maintain sorted data, making them suitable for applications needing dynamic sorting and ordered iteration. Hash Tables offer average constant-time complexity for insertion, deletion, and search operations but lack order, making them ideal for scenarios prioritizing fast access and lookup over sorted data.
Binary Search Tree Infographic
 libterm.com
libterm.com