Optimization enhances the efficiency and effectiveness of processes, products, or systems by refining key variables to achieve the best possible outcome. Leveraging advanced algorithms and data analysis, optimization drives better decision-making and resource allocation. Discover how optimizing your strategies can lead to significant improvements by reading the full article.
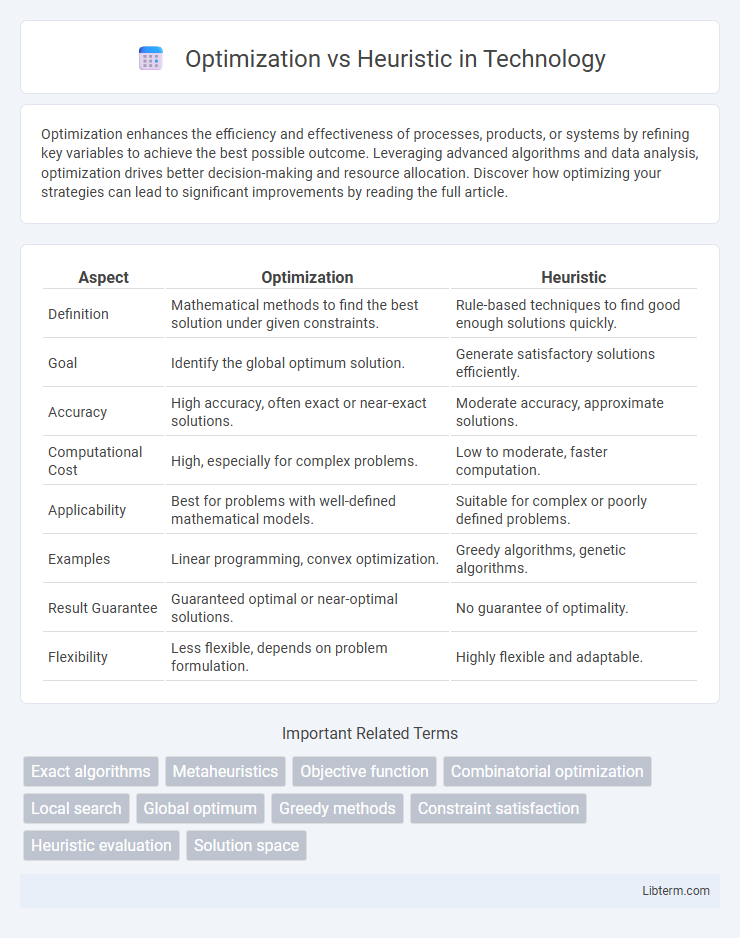
Table of Comparison
| Aspect | Optimization | Heuristic |
|---|---|---|
| Definition | Mathematical methods to find the best solution under given constraints. | Rule-based techniques to find good enough solutions quickly. |
| Goal | Identify the global optimum solution. | Generate satisfactory solutions efficiently. |
| Accuracy | High accuracy, often exact or near-exact solutions. | Moderate accuracy, approximate solutions. |
| Computational Cost | High, especially for complex problems. | Low to moderate, faster computation. |
| Applicability | Best for problems with well-defined mathematical models. | Suitable for complex or poorly defined problems. |
| Examples | Linear programming, convex optimization. | Greedy algorithms, genetic algorithms. |
| Result Guarantee | Guaranteed optimal or near-optimal solutions. | No guarantee of optimality. |
| Flexibility | Less flexible, depends on problem formulation. | Highly flexible and adaptable. |
Understanding Optimization and Heuristics
Optimization involves systematically finding the best solution from a set of feasible options by maximizing or minimizing an objective function under given constraints. Heuristics provide approximate solutions through rule-based or experience-driven methods, trading accuracy for faster computation in complex or uncertain problem spaces. Understanding optimization requires knowledge of mathematical programming and algorithmic strategies, while heuristics rely on domain expertise and intuitive shortcuts to improve problem-solving efficiency.
Key Differences Between Optimization and Heuristics
Optimization algorithms aim to find the best possible solution by exhaustively exploring the entire search space, often guaranteeing optimality but requiring significant computational resources. Heuristics provide approximate solutions through rule-based or experience-driven methods, prioritizing speed and practicality over guaranteed optimality. The key difference lies in optimization's emphasis on solution quality and completeness versus heuristics' focus on efficiency and feasibility in complex or time-constrained problems.
Mathematical Foundations of Optimization
Optimization relies on rigorous mathematical foundations involving calculus, linear algebra, and convex analysis to systematically identify the best solution from a feasible set. These methods use precise objective functions and constraints to guarantee optimality under defined conditions. Heuristic approaches, in contrast, bypass strict mathematical formulations and aim for near-optimal solutions through rule-based or iterative strategies without formal guarantees.
Heuristic Methods: Principles and Applications
Heuristic methods utilize rule-based approaches and experience-driven techniques to find satisfactory solutions in complex optimization problems where exact methods are computationally infeasible. These techniques, including genetic algorithms, simulated annealing, and tabu search, efficiently explore large search spaces by prioritizing promising solution regions through adaptive learning and iterative improvement. Widely applied in fields such as logistics, scheduling, and artificial intelligence, heuristic methods balance solution quality and computational effort, enabling practical problem-solving in dynamic and large-scale environments.
When to Choose Optimization Techniques
Optimization techniques are ideal when precise, quantifiable goals and well-defined constraints exist, enabling exact or near-exact solutions through mathematical models like linear programming or convex optimization. When problem complexity allows for clear objective functions and sufficient computational resources are available, optimization provides guaranteed optimality or bounds on solution quality. Choose optimization techniques in scenarios requiring rigorously validated results, such as supply chain logistics, resource allocation, or network design, where solution accuracy outweighs computational expense.
Advantages and Limitations of Heuristics
Heuristics offer the advantage of significantly faster problem-solving by using practical rules or shortcuts, making them ideal for complex or large-scale optimization problems where exact methods are computationally expensive. They provide good-enough solutions within reasonable time frames but lack guarantees of finding the global optimum, often leading to suboptimal or approximate results. Limitations include sensitivity to problem structure and potential inconsistency, making heuristics less reliable for problems requiring precise or provably optimal solutions.
Real-World Examples: Optimization vs Heuristic Solutions
Optimization techniques, such as linear programming, are used in supply chain management to minimize costs and maximize efficiency by finding the best solution from all feasible options. Heuristic methods, like genetic algorithms or simulated annealing, provide practical solutions for complex problems like scheduling airline crews or vehicle routing where exact optimization is computationally infeasible. Real-world applications demonstrate optimization's strength in precise resource allocation, while heuristics excel in delivering near-optimal results quickly under uncertainty or large-scale conditions.
Performance Comparison: Efficiency and Accuracy
Optimization algorithms typically provide higher accuracy by systematically exploring the solution space, ensuring convergence to near-optimal results, but often require more computational resources and time. Heuristic methods prioritize efficiency, delivering faster solutions with reduced computational cost by using problem-specific rules or approximations, which may sacrifice some accuracy. Performance comparison reveals that optimization excels in precision for complex problems, while heuristics outperform in speed and scalability for large or real-time applications.
Hybrid Approaches: Combining Optimization and Heuristic Methods
Hybrid approaches that combine optimization and heuristic methods leverage the strengths of both to enhance problem-solving efficiency and solution quality. By integrating exact optimization techniques with heuristic algorithms, these methods effectively balance exploration and exploitation, addressing complex, large-scale problems that are computationally challenging. This synergy improves convergence speed and yields near-optimal solutions in domains such as scheduling, routing, and resource allocation.
Future Trends in Problem-Solving Strategies
Optimization techniques leverage mathematical models and algorithms to find the best solution among many, while heuristics rely on rule-based approaches to quickly generate good-enough solutions. Future trends emphasize hybrid methods combining optimization's precision with heuristics' speed, enhanced by advancements in artificial intelligence and machine learning. These innovations are set to revolutionize problem-solving strategies by enabling adaptive, scalable, and real-time decision-making across complex domains.
Optimization Infographic
 libterm.com
libterm.com