Statistical methods are essential tools for collecting, analyzing, and interpreting data to uncover meaningful patterns and make informed decisions. Understanding the appropriate techniques, such as regression analysis, hypothesis testing, and variance analysis, empowers you to extract valuable insights from complex datasets. Explore the rest of this article to deepen your knowledge of key statistical methods and their practical applications.
Table of Comparison
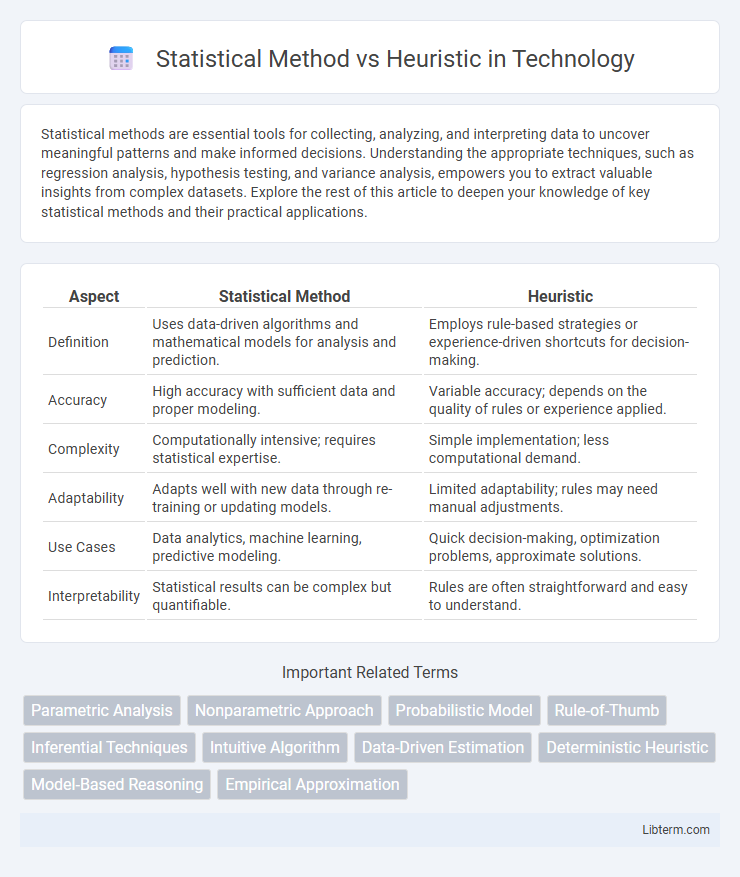
| Aspect | Statistical Method | Heuristic |
|---|---|---|
| Definition | Uses data-driven algorithms and mathematical models for analysis and prediction. | Employs rule-based strategies or experience-driven shortcuts for decision-making. |
| Accuracy | High accuracy with sufficient data and proper modeling. | Variable accuracy; depends on the quality of rules or experience applied. |
| Complexity | Computationally intensive; requires statistical expertise. | Simple implementation; less computational demand. |
| Adaptability | Adapts well with new data through re-training or updating models. | Limited adaptability; rules may need manual adjustments. |
| Use Cases | Data analytics, machine learning, predictive modeling. | Quick decision-making, optimization problems, approximate solutions. |
| Interpretability | Statistical results can be complex but quantifiable. | Rules are often straightforward and easy to understand. |
Introduction to Statistical Methods and Heuristics
Statistical methods involve systematic collection, analysis, and interpretation of data using probabilistic models to make informed decisions or predictions. Heuristics are experience-based techniques or rules of thumb designed to produce solutions quickly when full data or computational resources are unavailable. Introduction to statistical methods emphasizes accuracy and reliability through formal algorithms, while heuristics prioritize speed and practicality in problem-solving scenarios.
Defining Statistical Methods
Statistical methods involve the systematic collection, analysis, interpretation, and presentation of data to identify patterns and make inferences based on probability theories and mathematical principles. These methods prioritize accuracy, reproducibility, and formal models to quantify uncertainty and test hypotheses within structured datasets. In contrast to heuristic approaches, statistical techniques rely on rigorous algorithms that optimize decision-making through measurable evidence rather than rule-of-thumb shortcuts.
Understanding Heuristic Techniques
Heuristic techniques rely on experience-based rules and shortcuts to solve complex problems quickly when statistical methods demand extensive data and computation. These methods prioritize efficiency and practical solutions over exact accuracy, making them ideal for real-time decision-making in uncertain environments. Understanding heuristic techniques involves grasping their role in approximating optimal outcomes by simplifying the search space and leveraging domain-specific knowledge.
Key Differences: Statistical Method vs Heuristic
Statistical methods rely on mathematical models and probability theory to analyze data, enabling precise predictions and quantifiable uncertainty assessments. Heuristics are rule-based approaches or mental shortcuts that provide quick solutions without guaranteed accuracy, often used when data is incomplete or computational resources are limited. The key difference lies in statistical methods' foundation on rigorous data analysis versus heuristics' reliance on practical experience and approximate problem-solving.
Use Cases for Statistical Methods
Statistical methods excel in use cases involving large datasets where patterns, trends, and relationships need to be quantified and validated, such as in predictive modeling, risk assessment, and quality control. They provide robust frameworks for hypothesis testing, probability estimation, and uncertainty quantification, making them ideal for scientific research, market analysis, and healthcare data evaluation. These methods enable decision-making based on empirical evidence, enhancing accuracy and reliability in domains requiring statistical inference and data-driven insights.
Use Cases for Heuristic Approaches
Heuristic approaches excel in use cases where quick decision-making is essential despite incomplete or uncertain data, such as real-time system troubleshooting and customer service chatbots. They are particularly effective in complex optimization problems like routing, scheduling, and puzzle-solving where exhaustive statistical analysis is computationally impractical. Heuristics often complement statistical methods by providing approximate solutions that guide further detailed analysis in dynamic environments.
Advantages and Limitations of Statistical Methods
Statistical methods offer robust data analysis, providing quantifiable insights and rigorously tested models that enhance predictive accuracy and objectivity in decision-making. Their advantages include handling large datasets, identifying patterns, and enabling hypothesis testing with measurable confidence levels. Limitations arise from assumptions about data distribution, sensitivity to outliers, and potential challenges in interpreting complex statistical models without domain expertise.
Pros and Cons of Heuristic Strategies
Heuristic strategies offer quick, cost-effective decision-making by using rules of thumb that simplify complex problems, making them ideal for scenarios with limited data or time constraints. However, they can lead to biased or suboptimal solutions due to oversimplification and lack of rigorous validation, unlike statistical methods that provide more precise, data-driven inferences. Despite this, heuristics excel in adaptability and ease of implementation, making them valuable in dynamic environments where statistical models may be too resource-intensive.
Choosing Between Statistical Method and Heuristic
Choosing between statistical methods and heuristics depends on the complexity of the problem and the availability of data. Statistical methods offer precise, data-driven insights ideal for large datasets and probabilistic models, while heuristics provide quicker, experience-based solutions suited for scenarios with limited data or the need for rapid decision-making. Evaluating the trade-off between computational cost and accuracy is crucial in selecting the appropriate approach.
Future Trends in Data Analysis: Statistical and Heuristic Methods
Future trends in data analysis emphasize the integration of statistical methods with heuristic approaches to leverage the strengths of both, enabling more accurate predictions and adaptive problem-solving. Machine learning algorithms are increasingly combining statistical inference with heuristic optimizations to handle complex, high-dimensional datasets efficiently. This hybridization enhances model interpretability and scalability, driving advancements in real-time decision-making and automated analytics across diverse industries.
Statistical Method Infographic
 libterm.com
libterm.com