Partially Homomorphic Encryption (PHE) allows computations to be performed on encrypted data without decrypting it, preserving privacy while enabling data processing. This cryptographic technique supports specific operations, such as addition or multiplication, making it useful for secure data analysis in cloud computing and privacy-preserving protocols. Discover how PHE can protect Your sensitive information in various real-world applications by exploring the rest of the article.
Table of Comparison
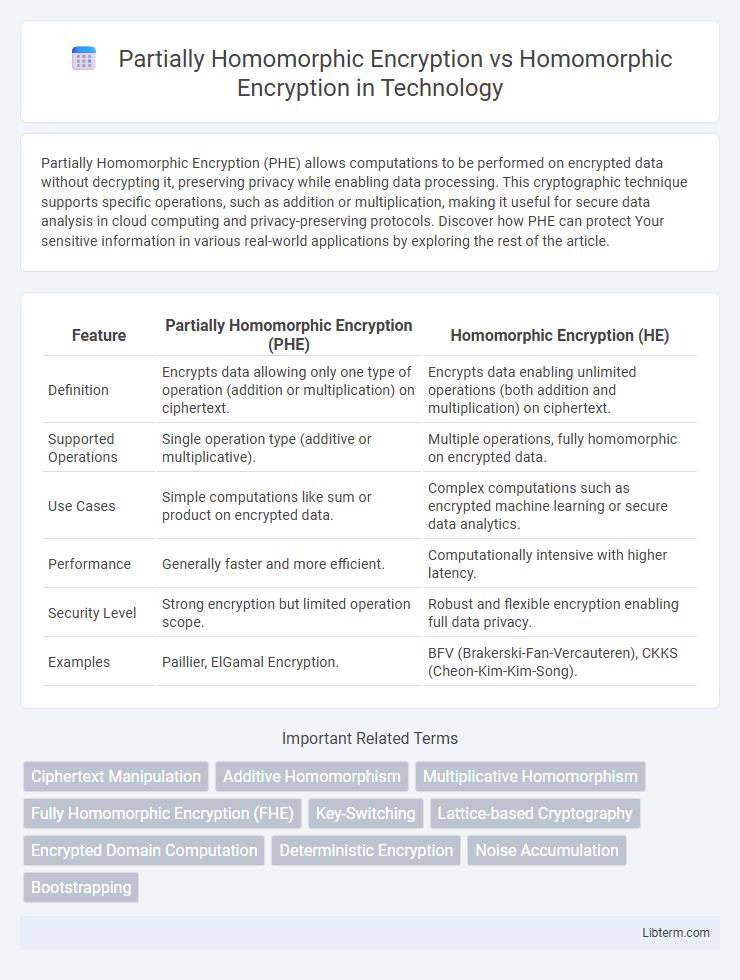
| Feature | Partially Homomorphic Encryption (PHE) | Homomorphic Encryption (HE) |
|---|---|---|
| Definition | Encrypts data allowing only one type of operation (addition or multiplication) on ciphertext. | Encrypts data enabling unlimited operations (both addition and multiplication) on ciphertext. |
| Supported Operations | Single operation type (additive or multiplicative). | Multiple operations, fully homomorphic on encrypted data. |
| Use Cases | Simple computations like sum or product on encrypted data. | Complex computations such as encrypted machine learning or secure data analytics. |
| Performance | Generally faster and more efficient. | Computationally intensive with higher latency. |
| Security Level | Strong encryption but limited operation scope. | Robust and flexible encryption enabling full data privacy. |
| Examples | Paillier, ElGamal Encryption. | BFV (Brakerski-Fan-Vercauteren), CKKS (Cheon-Kim-Kim-Song). |
Introduction to Homomorphic Encryption
Homomorphic encryption enables computations on encrypted data without decryption, preserving privacy and security. Partially homomorphic encryption supports a limited set of operations, such as addition or multiplication, while fully homomorphic encryption allows arbitrary computations on ciphertexts. This technology is crucial for secure data processing in cloud computing, enabling encrypted queries and machine learning on sensitive information.
Understanding Partially Homomorphic Encryption
Partially Homomorphic Encryption (PHE) enables specific algebraic operations, such as addition or multiplication, to be performed directly on encrypted data without decryption, providing data privacy during computation. Unlike Fully Homomorphic Encryption (FHE), which supports arbitrary operations on ciphertexts, PHE offers limited functionality but with lower computational overhead and increased efficiency. Understanding PHE is crucial for applications requiring secure data processing with constrained operation types, such as encrypted voting or secure database queries.
What is Fully Homomorphic Encryption?
Fully Homomorphic Encryption (FHE) enables computation on encrypted data without decryption, preserving privacy throughout complex operations. Unlike Partially Homomorphic Encryption (PHE), which supports only specific types of operations like addition or multiplication, FHE supports arbitrary computation on ciphertexts, allowing for secure data processing in cloud computing and sensitive applications. This capability makes FHE a powerful tool for confidential data analysis, secure multiparty computations, and privacy-preserving machine learning.
Key Differences Between Partially and Fully Homomorphic Encryption
Partially Homomorphic Encryption (PHE) supports only specific algebraic operations, such as addition or multiplication, on encrypted data, enabling limited homomorphic computations. Fully Homomorphic Encryption (FHE) allows arbitrary computations by supporting both addition and multiplication on ciphertexts, providing complete flexibility for encrypted data processing. The key difference lies in FHE's ability to execute complex functions homomorphically, while PHE is restricted to simpler, predefined operations, impacting their practical applications and computational overhead.
Encryption Algorithms and Supported Operations
Partially Homomorphic Encryption (PHE) algorithms, such as RSA and Paillier, support either additive or multiplicative operations on ciphertexts, enabling limited computation without decrypting data. Fully Homomorphic Encryption (FHE) algorithms, including schemes based on lattice problems like Gentry's construction, allow arbitrary computations by supporting both addition and multiplication on encrypted data. The main difference lies in PHE's restriction to a single operation type, while FHE enables comprehensive encrypted data processing, crucial for secure cloud computing and privacy-preserving applications.
Security Implications and Threat Models
Partially Homomorphic Encryption (PHE) supports operations on encrypted data but is limited to either addition or multiplication, offering a narrower attack surface compared to Fully Homomorphic Encryption (FHE), which enables arbitrary computations on ciphertexts but introduces increased complexity and potential vulnerabilities. The security implications of PHE typically involve simpler threat models focused on specific operation preservation, while FHE requires robust defenses against advanced cryptanalysis due to its broader operational capabilities. Threat models for FHE often consider side-channel attacks and ciphertext manipulation risks, necessitating more extensive security mechanisms to maintain confidentiality and integrity in practical applications.
Performance and Computational Overhead
Partially Homomorphic Encryption (PHE) supports specific algebraic operations on ciphertexts, offering significantly lower computational overhead compared to Fully Homomorphic Encryption (FHE), which enables arbitrary computations but incurs substantial performance penalties. The limited operation set in PHE allows for faster encryption, decryption, and evaluation processes, making it suitable for practical applications requiring efficiency. In contrast, FHE's complex bootstrapping procedures and high computational demands result in slower performance, restricting its widespread real-time adoption.
Real-World Applications and Use Cases
Partially Homomorphic Encryption (PHE) enables specific mathematical operations such as addition or multiplication on encrypted data, making it suitable for applications like secure voting systems and encrypted statistical analysis where limited computation is sufficient. In contrast, Fully Homomorphic Encryption (FHE) supports arbitrary computations on ciphertexts, empowering complex real-world use cases such as privacy-preserving machine learning, secure cloud computing, and confidential data analytics. PHE's efficiency advantages favor scenarios with predefined operations, while FHE's versatility addresses secure multiparty computations and advanced cryptographic protocols requiring comprehensive data processing.
Limitations and Challenges
Partially Homomorphic Encryption (PHE) supports either additive or multiplicative operations on ciphertexts but cannot perform both, limiting its applicability in complex computations. Homomorphic Encryption (HE), including Fully Homomorphic Encryption (FHE), allows arbitrary computations on encrypted data but faces significant challenges due to high computational overhead and large ciphertext sizes. Both PHE and HE require advancements in efficiency and scalability to overcome practical deployment limitations in real-world privacy-preserving applications.
Future Trends in Homomorphic Encryption Technologies
Future trends in homomorphic encryption technologies emphasize expanding the efficiency and scalability of fully homomorphic encryption (FHE) schemes to enable practical real-world applications such as secure cloud computing and privacy-preserving machine learning. Researchers are exploring hybrid models combining partially homomorphic encryption (PHE) with FHE to optimize performance by leveraging PHE's efficiency for specific operations while maintaining FHE's broader computational capabilities. Advances in algorithmic designs, hardware acceleration, and standardized protocols are accelerating adoption, promoting more robust privacy solutions for data analytics and secure multi-party computations.
Partially Homomorphic Encryption Infographic
 libterm.com
libterm.com