Extrapolation is a statistical technique used to estimate unknown values by extending a known sequence of data beyond the observed range. This method relies on identifying patterns and trends within existing data to make informed predictions about future or unseen points. Explore the rest of the article to understand how extrapolation can enhance your data analysis skills.
Table of Comparison
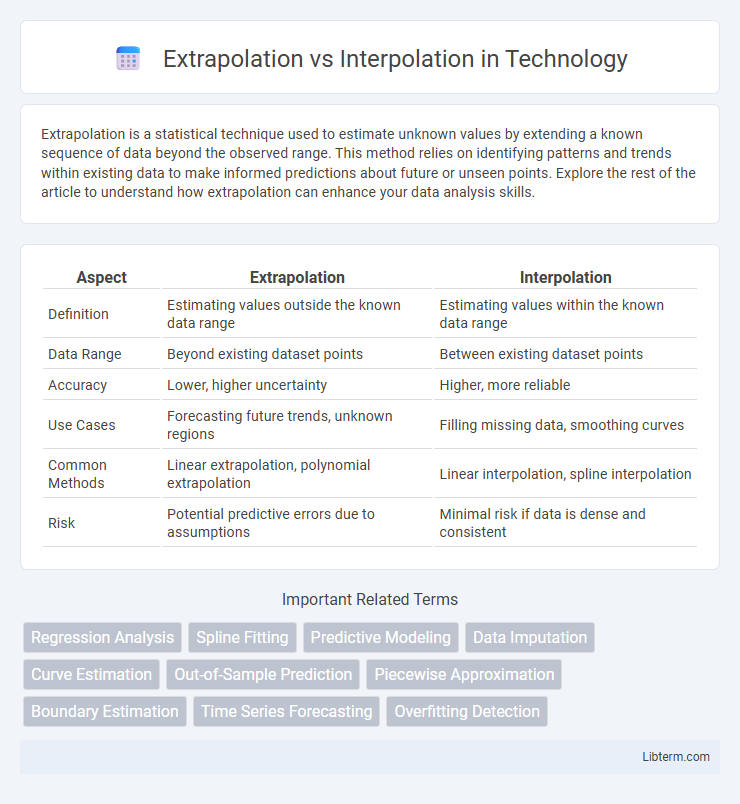
| Aspect | Extrapolation | Interpolation |
|---|---|---|
| Definition | Estimating values outside the known data range | Estimating values within the known data range |
| Data Range | Beyond existing dataset points | Between existing dataset points |
| Accuracy | Lower, higher uncertainty | Higher, more reliable |
| Use Cases | Forecasting future trends, unknown regions | Filling missing data, smoothing curves |
| Common Methods | Linear extrapolation, polynomial extrapolation | Linear interpolation, spline interpolation |
| Risk | Potential predictive errors due to assumptions | Minimal risk if data is dense and consistent |
Understanding Extrapolation and Interpolation
Extrapolation estimates values beyond the known data range by extending existing trends, which can introduce higher uncertainty due to lack of reference points. Interpolation calculates values within the range of known data points, typically resulting in more accurate and reliable predictions. Understanding the distinction helps in selecting appropriate methods for data analysis, modeling, and forecasting across scientific and engineering applications.
Key Differences Between Extrapolation and Interpolation
Interpolation estimates unknown values within the range of known data points, ensuring higher accuracy by relying on existing trends. Extrapolation predicts values beyond the known data range, often introducing greater uncertainty due to assumptions about trends continuing outside observed limits. The core difference lies in interpolation's bounded data scope versus extrapolation's use of data extensions, impacting reliability and risk in predictions.
Mathematical Definitions and Formulas
Interpolation estimates values within the range of known data points using functions such as linear interpolation: \( y = y_0 + \frac{(x - x_0)(y_1 - y_0)}{(x_1 - x_0)} \), where \((x_0, y_0)\) and \((x_1, y_1)\) are data points. Extrapolation predicts values outside the given data range by extending the fitted function, often using polynomial or linear models beyond observed intervals. Both methods rely on constructing approximating functions \( f(x) \) for unknown points \( x \), where interpolation \( x \in [x_0, x_n] \) and extrapolation \( x \notin [x_0, x_n] \).
Real-World Applications of Extrapolation
Extrapolation is frequently used in real-world applications such as financial forecasting, climate modeling, and engineering to predict future values based on existing data trends beyond the observed range. Unlike interpolation, which estimates values within the data set bounds, extrapolation carries higher uncertainty but is essential for long-term planning and risk assessment. Industries leverage extrapolation techniques to anticipate market behaviors, environmental changes, and system performances over extended periods.
Real-World Applications of Interpolation
Interpolation is widely used in engineering and meteorology to estimate unknown values within the range of known data points, such as predicting temperature at unsampled locations or generating smooth curves from discrete sensor readings. Geographic Information Systems (GIS) apply interpolation techniques like Kriging and inverse distance weighting to create continuous surface maps from scattered spatial data. In finance, interpolation helps estimate interest rates and bond prices by filling gaps within observed market data to support more precise risk assessment and investment decisions.
Advantages and Limitations of Extrapolation
Extrapolation extends data trends beyond the known dataset, enabling predictions outside observed ranges but often with increased uncertainty and risk of inaccuracy. Its advantage lies in forecasting future or unknown values, critical in fields like finance or climate modeling where data is limited. However, extrapolation's reliability diminishes as it assumes existing patterns continue unchanged, which may not reflect real-world complexities or abrupt changes.
Advantages and Limitations of Interpolation
Interpolation offers the advantage of estimating unknown values within the range of a discrete set of known data points, providing more accurate and reliable predictions compared to extrapolation, which projects data beyond the observed range. It is widely used in fields such as engineering, finance, and meteorology, where predicting intermediate data is crucial. However, interpolation assumes the data behaves smoothly between points and can produce inaccuracies if the underlying function is highly nonlinear or if data points are sparse.
Common Errors in Data Prediction
Common errors in data prediction arise when extrapolation assumes trends beyond known data points, often leading to inaccurate forecasts due to unvalidated assumptions. Interpolation errors occur when predictions between data points fail to account for underlying data variability or nonlinear patterns. Misapplication of both methods without proper validation or understanding of data behavior results in significant reliability issues in predictive modeling.
Best Practices for Accurate Data Estimation
Extrapolation and interpolation are essential techniques for estimating unknown data points based on existing datasets, where interpolation predicts values within the range of known data, and extrapolation extends beyond that range. Best practices for accurate data estimation emphasize using interpolation when possible due to its lower risk of error, applying appropriate mathematical models like polynomial or spline functions tailored to the dataset's behavior, and validating results with cross-validation or residual analysis. Ensuring data quality, understanding underlying trends, and avoiding overfitting are critical to minimizing bias and improving estimation accuracy in both methods.
Extrapolation vs Interpolation: Which to Use and When
Interpolation estimates values within the range of known data points, providing accurate and reliable predictions for missing data between observed values. Extrapolation predicts data outside the known range, often involving higher uncertainty and risk due to assumptions beyond available information. Use interpolation when your target falls within the existing dataset limits, and choose extrapolation cautiously when forecasting beyond known data, ensuring awareness of potential errors and model limitations.
Extrapolation Infographic
 libterm.com
libterm.com