Algorithmic processes leverage mathematical formulas and step-by-step procedures to solve complex problems efficiently. Understanding these techniques can enhance your ability to develop optimized solutions across various fields, from computer science to data analysis. Explore the rest of the article to discover how algorithmic strategies can transform your approach to problem-solving.
Table of Comparison
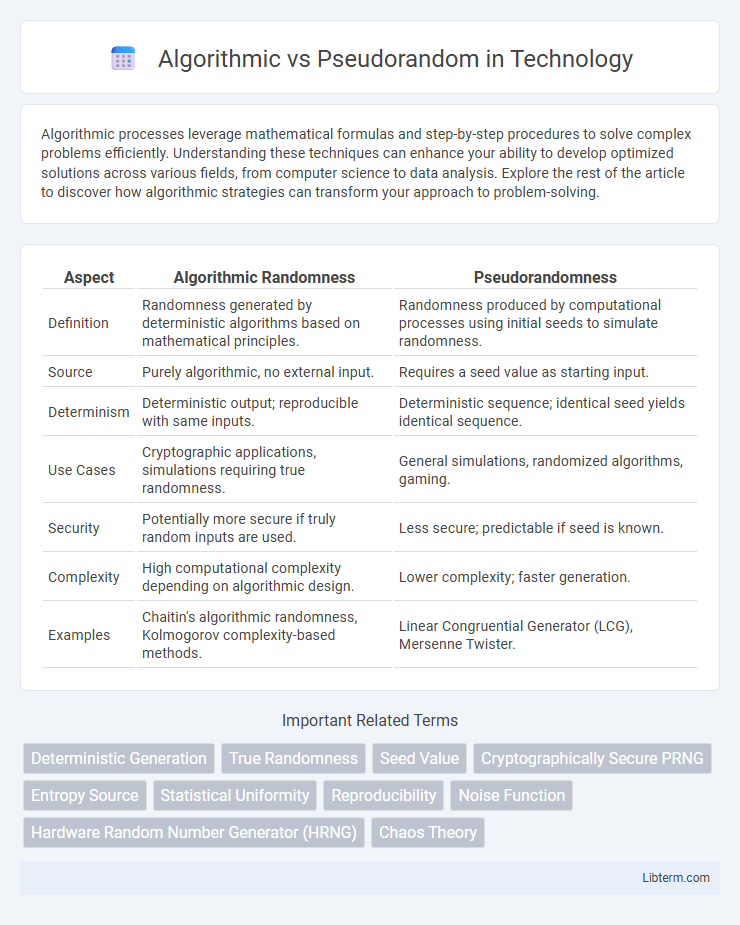
| Aspect | Algorithmic Randomness | Pseudorandomness |
|---|---|---|
| Definition | Randomness generated by deterministic algorithms based on mathematical principles. | Randomness produced by computational processes using initial seeds to simulate randomness. |
| Source | Purely algorithmic, no external input. | Requires a seed value as starting input. |
| Determinism | Deterministic output; reproducible with same inputs. | Deterministic sequence; identical seed yields identical sequence. |
| Use Cases | Cryptographic applications, simulations requiring true randomness. | General simulations, randomized algorithms, gaming. |
| Security | Potentially more secure if truly random inputs are used. | Less secure; predictable if seed is known. |
| Complexity | High computational complexity depending on algorithmic design. | Lower complexity; faster generation. |
| Examples | Chaitin's algorithmic randomness, Kolmogorov complexity-based methods. | Linear Congruential Generator (LCG), Mersenne Twister. |
Introduction to Randomness: Algorithmic vs Pseudorandom
Randomness in computational contexts distinguishes between true algorithmic randomness, which is inherently unpredictable and derived from natural processes, and pseudorandomness, generated by deterministic algorithms that simulate random sequences. Algorithmic randomness is characterized by incompressible and patternless sequences, making it essential for tasks demanding high entropy, whereas pseudorandom generators rely on initial seeds and produce sequences that appear random but are ultimately predictable if the seed or algorithm is known. Understanding the differences informs cryptography, simulations, and numerical methods where the quality of randomness directly impacts security and accuracy.
Defining Algorithmic Randomness
Algorithmic randomness refers to sequences that cannot be generated by any shorter computer program, indicating true randomness based on incompressibility and unpredictability. It contrasts with pseudorandom sequences, which are produced by deterministic algorithms and can be reproduced given the initial seed. The concept of algorithmic randomness is formalized through Martin-Lof randomness and Kolmogorov complexity, emphasizing that truly random sequences lack effective patterns or compressible structure.
Understanding Pseudorandomness
Pseudorandomness refers to number sequences generated by deterministic algorithms that mimic true randomness with high statistical similarity, crucial in cryptography and simulations. Unlike truly random sequences derived from physical phenomena, pseudorandom sequences rely on initial seeds and complex algorithms like the Mersenne Twister or linear congruential generators. Understanding pseudorandomness involves analyzing properties such as periodicity, unpredictability, and distribution uniformity to ensure reliability in practical applications.
Key Differences Between Algorithmic and Pseudorandom
Algorithmic randomness is rooted in complex deterministic processes that generate sequences indistinguishable from true randomness by any algorithmic means, while pseudorandomness employs deterministic algorithms to produce sequences that appear random but are reproducible with the same initial seed. Algorithmic random sequences have maximal Kolmogorov complexity, meaning they cannot be compressed or predicted, whereas pseudorandom sequences have lower complexity and can be efficiently generated and predicted if the algorithm and seed are known. The core difference lies in unpredictability and compressibility: algorithmic randomness is truly incompressible and unpredictable, whereas pseudorandomness is computationally feasible but relies on initial conditions for reproduction.
Sources and Generation Methods
Algorithmic randomness relies on deterministic procedures or algorithms such as linear congruential generators, which produce sequences based on initial seed values and mathematical formulas. Pseudorandom number generators (PRNGs) utilize fixed algorithms that simulate randomness but are inherently predictable if the seed and method are known. True randomness stems from physical sources like radioactive decay or atmospheric noise, where entropy is harnessed to generate nondeterministic, non-reproducible sequences.
Real-World Applications of Algorithmic Randomness
Algorithmic randomness is vital in cryptographic security, where truly unpredictable sequences prevent unauthorized data breaches and ensure secure communication protocols. In simulations and modeling, algorithmic randomness provides statistically sound, reproducible random inputs that enhance the accuracy of system behavior predictions. Furthermore, algorithmic randomness underpins randomized algorithms in machine learning, improving optimization and generalization by introducing controlled variability in training data.
Practical Uses of Pseudorandom Generators
Pseudorandom generators are essential for cryptographic applications, enabling secure key generation and encryption processes by producing sequences that appear random but are reproducible with a seed. In simulations and modeling, pseudorandom numbers ensure consistency and repeatability, allowing researchers to verify results and debug algorithms effectively. Practical uses also extend to randomized algorithms in computer science, where pseudorandomness optimizes performance and resource usage without compromising unpredictability.
Security Implications: Algorithmic vs Pseudorandom
Algorithmic random number generators (RNGs) produce sequences deterministically based on initial seeds, posing risks in cryptographic applications if seeds are compromised, making patterns predictable. Pseudorandom number generators (PRNGs) improve security by employing complex algorithms that simulate randomness but still rely on entropy sources and seed security to prevent vulnerabilities. True security in cryptographic systems depends on robust entropy generation and resistant PRNG algorithms to mitigate attack vectors exploiting weak randomness.
Testing and Validation of Randomness
Testing and validation of randomness in algorithmic versus pseudorandom number generators (PRNGs) rely heavily on statistical tests such as the Diehard tests and NIST SP 800-22 suite. Algorithmic randomness is theoretically proven but often non-computable, making empirical testing crucial for PRNGs to ensure the absence of detectable patterns or biases. High-quality PRNGs pass rigorous randomness tests to confirm their suitability for cryptographic applications and simulations, differentiating them from weaker algorithmic approaches that may fail to meet strict entropy and unpredictability criteria.
Choosing Between Algorithmic and Pseudorandom Approaches
Choosing between algorithmic and pseudorandom approaches depends on the required balance between predictability and randomness quality. Algorithmic methods offer reproducibility and efficiency in simulations, while pseudorandom techniques generate sequences with higher unpredictability suitable for cryptographic applications. Evaluating the specific use case's demands on randomness quality, performance, and security guides the optimal selection.
Algorithmic Infographic
 libterm.com
libterm.com